4.2. Плотность циркуляции векторного поля

Пусть в векторном поле на поверхности дан замкнутый контур L, заключающий в себе точку М (рис. 4.2).

- единичный вектор нормали к

поверхности в т. М;

.

Пусть - площадь поверхности,

ограниченной контуром L.

Рис. 4.3

Определение 4.2.1. Плотностью циркуляции в точке М называется предел отношения циркуляции к площади поверхности при условии стягивания контура к точке М.

. (4.2)

В проекциях плотность циркуляции выражается в виде .

Если подынтегральное выражение преобразовать по формуле Стокса, то получим

(4.3)

Частные производные вычислены в данной точке М.

5. Ротор векторного поля. Теорема стокса

В ВЕКТОРНОЙ ФОРМЕ

Определение 5.1. Ротор (или вихрь) векторного поля точки М обозначается и определяется формулой , (5.1)

где частные производные вычислены в точке М.

Для лучшего запоминания этот вектор можно записать в виде следующего символического определителя:

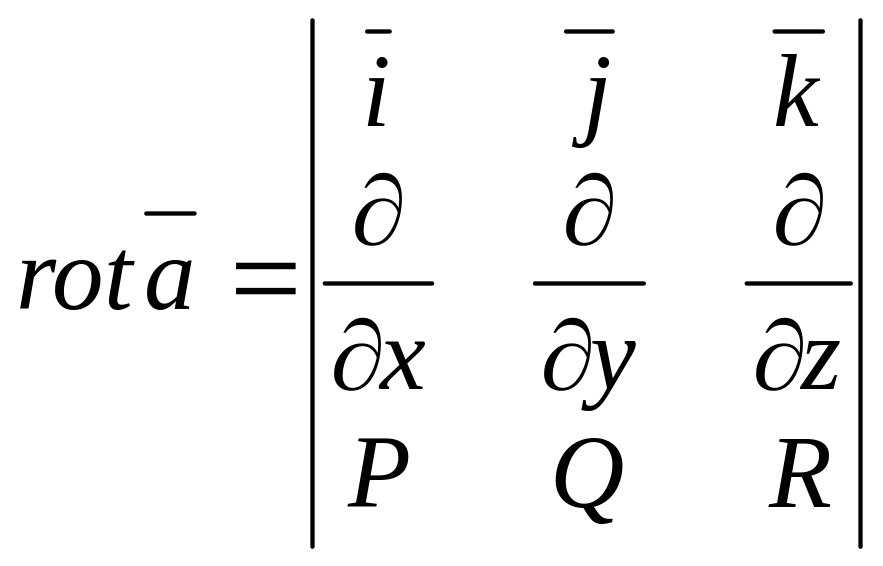(5.2)

Смысловое определение ротора вытекает из его связи с плотностью циркуляции поля; сравнивая формулы (4.3) и (5.1), можно записать

.

Если значение косинуса равно 1, то из последнего равенство . Таким образом, плотность циркуляции в точке М будет наибольшей в направлении ротора и равна его численному значению. Физический смысл ротора в поле скоростей заключается в том, что ротор представляет собой мгновенную угловую скорость вращения тела.

Пример 5.1. Найти ротор векторного поля .

Решение. Используя формулу (5.1), найдем проекции ротора

;

;

.

Следовательно, .

С помощью введенного можно записать формулу Стокса в векторной форме. Так как + ,

следовательно, в векторной форме это равенство имеет вид . (5.3)

Итак, поток вектора через ориентированную поверхность равен циркуляции вектора вдоль положительного направления

обхода контура L этой поверхности.

Пример 5.2. Найти циркуляцию векторного поля

по контуру , где , (рис. 5.1).

Решение. Найдем , используя символическую запись (5.2)

.

В качестве поверхности , натянутой на контур , возьмем круг (в плоскости ), тогда , . По формуле (5.3) найдем циркуляцию, вычислив двойной интеграл в полярных координатах:

;

Пример 5.3 Вычислить циркуляцию векторного поля : по контуру .

Решение. Вычислим, применив формулу Стокса (5.3). Найдем

.

В качестве поверхности берем часть плоскости , ограниченную контуром .

При пересечении цилиндра и плоскости получится эллипс. Поверхность (эллипс) проектируется на плоскость в круг. Тогда , (из уравнения плоскости ).

;

.