
- •1.Векторное поле. Векторные линии и их
- •2.1. Вычисление потока
- •2.1.1. Вычисление методом проектирования на одну
- •2.1.2. Вычисление потока методом проектирования
- •3. Дивергенция векторного поля.
- •3.1. Вычисление дивергенции
- •3.2. Формула Остроградского в векторной форме
- •4. Линейный интеграл в векторном поле.
- •4.1. Определение и вычисление циркуляции
- •4.2. Плотность циркуляции векторного поля
- •5. Ротор векторного поля. Теорема стокса
- •6. Классификация векторных полей
- •6.1. Безвихревое поле
- •6.2. Потенциальное поле
- •6.3. Соленоидальные поля
- •7. Задание для самостоятельной работы
- •Список литературы
2.1. Вычисление потока
2.1.1. Вычисление методом проектирования на одну
из координатных плоскостей
Пусть поверхность
задана уравнением
![]() .
.
Единичный вектор
нормали
![]() ,
но, как известно,
,
но, как известно,
![]() .
Следовательно,
.
Следовательно,
 .
.
Знак в правой части
берется так, чтобы получить нормальный
вектор
![]() именно к выбранной стороне поверхности.
именно к выбранной стороне поверхности.
Если поверхность
задана уравнением
![]() ,
то
,
то
![]() .
.
Знак «+» соответствует
выбору верхней стороны поверхности,
нормаль к которой образует острый угол
с осью
![]() и, следовательно, направляющий косинус
положителен.
и, следовательно, направляющий косинус
положителен.
Известно также,
что
![]() и
и
![]() .
.
Пусть поверхность
взаимно однозначно проектируется на
плоскость
в область
![]() ,
тогда вычисление потока векторного
поля через поверхность
сводится к вычислению двойного интеграла
,
тогда вычисление потока векторного
поля через поверхность
сводится к вычислению двойного интеграла
по области
:
![]() .
(2.2)
.
(2.2)
Аналогично, если
поверхность
взаимно однозначно проектируется на
плоскость
или
![]() ,
то поток вычисляется по формулам
,
то поток вычисляется по формулам
![]() ;
;
![]() .
.
Пример 2.1. Найти
поток векторного поля
![]() через поверхность конуса
через поверхность конуса
![]() и плоскость
и плоскость
![]() .
.
Решение. Обозначим
потоки векторного поля:
![]() через
через
 боковую
поверхность конуса
боковую
поверхность конуса
![]() и
и
![]() через плоскость
через плоскость
![]() .
.
Тогда весь поток П=П1 +П2 =
![]() .
.
Вычислим
.
Уравнение
![]() :
:
![]() .
.
Проекция вектора
![]() на ось
отрицательна.
на ось
отрицательна.
![]() ;
;
![]()
 .
.
Из выражения для (2.2.) найдем
![]() .
.
 .
.
Вычислим
.
Уравнения поверхности
![]() :
,
:
,
![]() ,
,
![]() (На поверхности
),
(На поверхности
),
![]() .
.
Следовательно,
![]() .
.
Пример 2.2. Найти
поток векторного поля
![]() через верхнюю сторону треугольника с
вершинами в точках
через верхнюю сторону треугольника с
вершинами в точках
![]() ,
,
![]() ,
,
![]() .
.
Решение. Уравнение
плоскости
![]() составим как уравнение
составим как уравнение
 плоскости,
проходящей через три точки
плоскости,
проходящей через три точки
![]() .
Следовательно,
.
Следовательно,
![]() ,
,
![]() .
.
![]()
![]() .
.

Пример 2.3. Вычислить поток векторного поля
![]()
через внешнюю
сторону однополостного гиперболоида
![]() ,ограниченного плоскостями
,ограниченного плоскостями
![]()
![]() .
.
Решение. Данная
поверхность проектируется взаимно
однозначно на плоскость
![]() в область
в область
![]() ,
ограниченную окружностями
,
ограниченную окружностями
![]() и
и
![]() .
.
Находим внешнюю
нормаль
![]() :
:
![]()
![]() .
.
Т .к.
образует с осью
тупой угол
.к.
образует с осью
тупой угол
![]() (рис.2.4),
то берем знак минус и, значит,
(рис.2.4),
то берем знак минус и, значит,
![]() .
.
Находим скалярное
произведение
![]()
![]() .
.
Применяя формулу
![]() ,
,
получим
Рис.2.4
![]() .
.
Переходя к полярным
координатам
![]() ,
,![]() ,
будем иметь
,
будем иметь

2.1.2. Вычисление потока методом проектирования
на все три координатные плоскости
Пусть поверхность взаимно однозначно проектируется на все три координатные плоскости:
![]()
Тогда поток
векторного поля
![]() равен
равен
 (2.3.)
(2.3.)
где знак перед
каждым из двойных интегралом берется
соответственно таким, каков знак
![]() ,
,
![]() ,
,
![]() на поверхности
.
на поверхности
.
Пример 2.3. Найти
поток векторного поля
![]() через треугольник, получаемый при
пересечении плоскости
с координатными плоскостями (выбор
указан на рис. 2.5).
через треугольник, получаемый при
пересечении плоскости
с координатными плоскостями (выбор
указан на рис. 2.5).
Р ешение.
Найдем
.
P[x(y,z),y,z]=(1-y-z)-2z=1-y-3z
(выразили
из уравнения плоскости)
ешение.
Найдем
.
P[x(y,z),y,z]=(1-y-z)-2z=1-y-3z
(выразили
из уравнения плоскости)
![]()
![]() .
.
По формуле (2.3) получим
Рис. 2.5
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]() .
.
При вычислении потока векторного поля через боковую поверхность кругового цилиндра или через сферу удобно пользоваться соответственно цилиндрическими или сферическими координатами.
Пример 2.4. Найти поток векторного поля
![]() через часть
сферической поверхности
через часть
сферической поверхности
![]() ,
расположенную в первом октанте.
,
расположенную в первом октанте.
Решение. Найдем
вектор- градиент
![]() ,
,
тогда единичный
вектор
![]() ;
;
![]() .
.
По условию задачи
поверхность находится в первом октанте,
т.е.
![]() ,
,
![]() ,
элемент площади в сферических координатах
равен
,
элемент площади в сферических координатах
равен
![]() .
Следовательно, поток через часть сферы
вычисляется по формуле
.
Следовательно, поток через часть сферы
вычисляется по формуле
![]() .
.
2.1.3. Вычисление потока методом введения
криволинейных координат на поверхности
В некоторых случаях при вычислении потока векторного поля через данную поверхность S возможно выбрать на самой поверхности простую систему координат, в которой удобно вычислять поток, не применяя проектирования на координатные плоскости.
Рассмотрим частные случаи.
Случай 1). Пусть
поверхность S
является частью кругового цилиндра
![]() ,
ограниченного поверхностями
,
ограниченного поверхностями
![]() и
и
![]() .
.
Полагая
![]() ,
будем иметь для данной поверхности
,
будем иметь для данной поверхности
![]() ,
,
![]() , а для элемента
площади dS
получаем следующее выражение (рис.
2.6.):
, а для элемента
площади dS
получаем следующее выражение (рис.
2.6.):
![]()
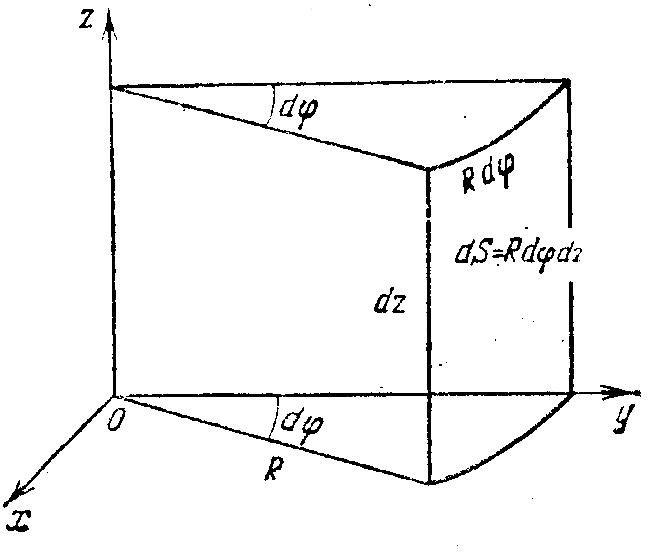 .
.
Тогда поток векторного поля a
через внешнюю сторону поверхности S
вычисляется по формуле
 ,
(2.4)
,
(2.4)
где Рис. 2.6
![]()
Пример 2.5. Вычислить поток радиуса-вектора
![]() через боковую
поверхность кругового цилиндра
через боковую
поверхность кругового цилиндра
![]() ,
ограниченного снизу плоскостью
,
ограниченного снизу плоскостью
![]() ,
а сверху – плоскостью
,
а сверху – плоскостью
![]() .
.
Р ешение.
В данном случае (рис. 2.7) имеем
ешение.
В данном случае (рис. 2.7) имеем
![]() .
.
Переходя к координатам на цилиндре
![]() ,
будем иметь
,
будем иметь
![]() ,
,
![]()
Согласно формуле (2.4) поток вектора r
будет равен
![]()
Но так как на цилиндре
![]() Рис.
2.7
Рис.
2.7
то
![]()
и,
следовательно,
![]()
Случай 2). Пусть
поверхность S является
частью сферы
![]() ,
ограниченной коническими поверхностями,
уравнения которых в сферических
координатах имеют вид
,
ограниченной коническими поверхностями,
уравнения которых в сферических
координатах имеют вид
![]() и
полуплоскостями
и
полуплоскостями
![]() .
.
Положим для точек данной сферы
![]()
г де
де
![]() .
.
Тогда для элемента площади dS полу- чим (рис. 2.7)
![]() .
.
В этом случае поток векторного поля а через внешнюю часть S сферы вычисляется по формуле
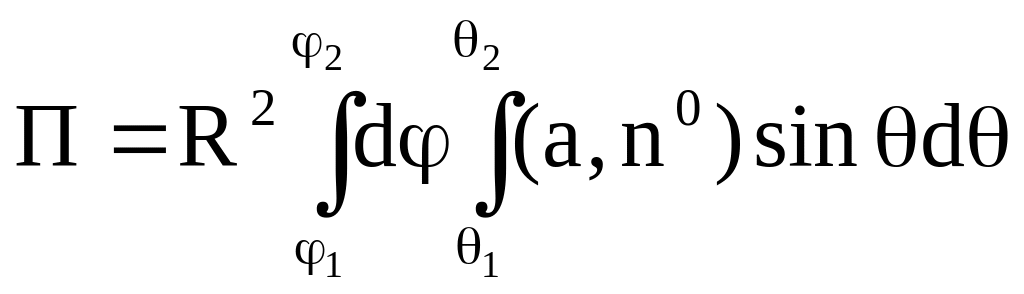 , ( 2.5)
, ( 2.5)
Рис. 2.8 где
![]()
Пример 2.6. Найти поток вектора
![]()
через
часть поверхности сферы
![]() ,
расположенную в первом октанте, в
область, где
,
расположенную в первом октанте, в
область, где
![]() .
.
Решение. В данном случае имеем
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
Введем
на сфере
координаты
![]() и
и
![]() так, что
так, что
![]()
Тогда
будет иметь
![]()
и, применяя формулу (2.5), получим
![]()
![]()
