
- •1.Векторное поле. Векторные линии и их
- •2.1. Вычисление потока
- •2.1.1. Вычисление методом проектирования на одну
- •2.1.2. Вычисление потока методом проектирования
- •3. Дивергенция векторного поля.
- •3.1. Вычисление дивергенции
- •3.2. Формула Остроградского в векторной форме
- •4. Линейный интеграл в векторном поле.
- •4.1. Определение и вычисление циркуляции
- •4.2. Плотность циркуляции векторного поля
- •5. Ротор векторного поля. Теорема стокса
- •6. Классификация векторных полей
- •6.1. Безвихревое поле
- •6.2. Потенциальное поле
- •6.3. Соленоидальные поля
- •7. Задание для самостоятельной работы
- •Список литературы
УФИМСКИЙ государственный НЕФТЯНОЙ технический Университет
Стерлитамакский филиал
Учебно-МЕТОДИЧЕСКоЕ пособие
по теме “Векторный анализ”
Уфа, 2003
Учебно-методическое пособие содержит основные сведения по векторному анализу, предусмотренные программой по высшей математике технического вуза. Предлагаемое методическое пособие рекомендуется для студентов дневного и вечернего отделения по специальностям 1705, 2103, 2903. Разработки являются средством управления и самоуправления учебной работой студентов в аудиторное и внеаудиторное время. Расчетные задания скомплектованы по степени сложности, что позволяет осуществить индивидуальный подход в обучении.
Составители: Григорьева Т. В., доц., канд. пед. наук
Рахматуллина Ф.Т., доц., канд. техн. наук
Жигалова О.В., ст. преподаватель
Седаева Л.С., ст. преподаватель
Рецензент Шулаев Н. С., проф., д-р техн. наук
©Уфимский государственный нефтяной технический
институт, 2002
1.Векторное поле. Векторные линии и их
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Определение 1.1.
Векторным полем точки М называется
векторная функция
![]() точки М вместе с областью ее определения.
точки М вместе с областью ее определения.
Задание векторного
пространственного поля равносильно
заданию трех скалярных функций
![]() ,
,
![]() ,
,
![]() ,
являющихся проекциями вектора
,
являющихся проекциями вектора
![]() на координатные оси. Примерами векторных
полей являются поле магнитной
напряженности, поле сил тяготения, поле
скоростей установившегося потока
жидкостей и т.д.
на координатные оси. Примерами векторных
полей являются поле магнитной
напряженности, поле сил тяготения, поле
скоростей установившегося потока
жидкостей и т.д.
Определение 1.2. Векторной линией поля называется такая линия, в каждой точке которой касательная совпадает с направлением вектора . Векторная линия обычно называется линией тока для поля скоростей, силовой линией – для силового поля.
Как известно,
направляющие косинусы касательной
пропорциональны дифференциалам
![]() ,
,
![]() ,
,
![]() .
Для нахождения векторных линий поля
векторов
.
Для нахождения векторных линий поля
векторов
![]() и
и
![]()
![]() ,
(1.1)
,
(1.1)
где
![]() - проекция вектора
на координатные оси.
- проекция вектора
на координатные оси.
Уравнения (1.1) называются дифференциальными уравнениями векторных линий поля . Если - непрерывно дифференцируемые функции и в точке М вектор отличен от нуля, то через точку М проходит одна определенная векторная линия поля .
Пример 1.1. Найти
векторные линии поля
![]() .
.
Решение.
Дифференциальные уравнения векторных
линий имеют вид
![]() или
или
![]() ,
,
![]() ;
;
![]() ,
.
Интегрируя, получим
,
.
Интегрируя, получим
![]() и
и
![]() ,
где
,
где
![]() и
и
![]() - произвольные постоянные. Векторными
линиями являются окружности, расположенные
в плоскостях, параллельных плоскости
- произвольные постоянные. Векторными
линиями являются окружности, расположенные
в плоскостях, параллельных плоскости
![]() и в самой плоскости
при
и в самой плоскости
при
![]() .
.
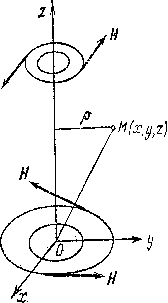
Пример 1.2. Найти векторные линии магнитного поля бесконечного проводника тока.
Решение. Будем
считать, что проводник направлен по
оси
![]() и в этом же направлении течет ток I
. Вектор напряженности H
магнитного поля, создаваемого током,
равен
и в этом же направлении течет ток I
. Вектор напряженности H
магнитного поля, создаваемого током,
равен
![]() , (1.2)
, (1.2)
где
![]() есть вектор тока,
есть вектор тока,
![]() - радиус-вектор точки
- радиус-вектор точки
![]() ,
,
![]() -
расстояние от оси провода до точки М.
Раскрывая векторное произведение
(1.2), получим
-
расстояние от оси провода до точки М.
Раскрывая векторное произведение
(1.2), получим
![]() .
.
Дифференциальные уравнения векторных линий:
![]() ,
,
откуда
![]() ,
Рис 1.
,
Рис 1.
т.е. векторные линии являются окружностями с центрами на оси (рис. 1).
2. ПОТОК ВЕКТОРНОГО ПОЛЯ ЧЕРЕЗ ПОВЕРХНОСТЬ
Определение 2.1.
Потоком П векторного поля
![]() через
через
двустороннюю
поверхность
![]() называется поверхностный интеграл
называется поверхностный интеграл
второго рода.
![]() ,
(2.1)
,
(2.1)
где
![]() - единичный вектор нормали к
,
указывающей её ориентацию;
- единичный вектор нормали к
,
указывающей её ориентацию;
![]() - элемент площади поверхности
;
- элемент площади поверхности
;
![]() - проекция вектора
на направление
- проекция вектора
на направление
![]() .
.
Дадим физическое
истолкование формулы (2.1). Пусть
![]() - скорость жидкости, протекающей через
произвольную (двустороннюю) поверхность
.
Рассмотрим разбиение
- скорость жидкости, протекающей через
произвольную (двустороннюю) поверхность
.
Рассмотрим разбиение
![]() поверхности на n
частей
поверхности на n
частей
![]() с площадками
с площадками
![]() .
Тогда произведение
.
Тогда произведение
![]() равно количеству жидкости, протекающей
через
равно количеству жидкости, протекающей
через
 поверхность
за единицу времени в
поверхность
за единицу времени в
направлении
вектора
![]() (рис.2.1).
(рис.2.1).
Интеграл
![]() ,
являющийся
,
являющийся
пределом интегральной суммы
![]() ,
дает полное количество жидкости,
протекающей в единицу времени через
в положительном направлении. Пусть
- поле скоростей в стационарном течении
жидкости, так что ее скорость
в точке М зависит лишь от М, но не зависит
от времени. Из сказанного выше следует,
что поток скорости через ориентированную
поверхность
за единицу времени в том направлении,
в котором ориентирована эта поверхность
(физический смысл потока).
,
дает полное количество жидкости,
протекающей в единицу времени через
в положительном направлении. Пусть
- поле скоростей в стационарном течении
жидкости, так что ее скорость
в точке М зависит лишь от М, но не зависит
от времени. Из сказанного выше следует,
что поток скорости через ориентированную
поверхность
за единицу времени в том направлении,
в котором ориентирована эта поверхность
(физический смысл потока).
