3. Расчетная часть.

Исходные данные для выполнения курсовой работы:

№ вари-анта	Тип цикла	Условия сравнения	Значения термодинамических параметров pi (МПА), vi (м3/кг), Тi (oК)				Характеристики цикла	Подведенное тепло q1(кДж/кг)
97	p	, q1	p1=0,114	Т1=319	p2=5,337	=1.35	не заданы	не задано

3.1.

При температуре 319⁰К (46⁰С) значения теплоемкостей воздуха:

С_v =⁰С =0,75158кДж/кг^оК;

С_p =⁰С =1,03838кДж/кг^оК.

Показатель адиабаты воздуха при температуре 319⁰К:

Основные термодинамические параметры в характерных точках заданного цикла.

точка 1:по заданнымиз уравнения состояния идеального газа найдём удельный объем:

.

точка 2: так как процесс 1-2 адиабатный, то из уравнения адиабаты следует, что

.

Из уравнения состояния идеального газа:

точка 3:

Из уравнения состояния идеального газа:

точка 4: из уравнения адиабаты для процесса 3-4 получаем:

.

Из уравнения состояния идеального газа:

Степень сжатия и степень предварительного расширения для этого цикла соответственно равны:

Термический КПД этого цикла:

Сравнение термического КПД цикла с подводом тепла при с КПД циклов с подводом тепла прии смешанным подводом тепла выполняется при заданных в задании условиях сравнения и значениях термодинамических параметров в исходной точке (), аналогичных с заданным циклом.

Для расчета термического КПД цикла с подводом тепла при принимаются заданными

В соответствии с условиями сравнения известны параметры в цикле:

точка 2: процесс 1-2 адиабатный, следовательно (используя уравнение связи между давлением и удельным объемом для адиабатного процесса):

Из уравнения состояния находим:

точка 3: .

Из уравнения состояния идеального газа находим:

точка 4: так кака процесс 3-4 адиабатный, то из уравнения адиабаты:

Из уравнения состояния находим: .

Степень сжатия и степень изохорного повышения давления для рассматриваемого (с подводом тепла при ) цикла будут, соответственно, равны: . В соответствии с (2.2) термический КПД рассматриваемого цикла:

.

Для расчета термического КПД цикла со смешанным подводом тепла считаются заданными В соответствии с условиями сравнения известны параметры в цикле:

точка 2: ;

точка 3: В силу того, что, то

Выберем для рассматриваемого цикла со смешанным подводом тепла Тогда из уравнения состояния:

точка 4 :

Из уравнения состояния идеального газа:

точка5: учитывая, что процесс 4-5 адиабатный, получим:

а из уравнения состояния:

При этих значениях параметров в характерных точках цикла его характеристики будут равны: степень сжатия: степень изохорного повышения давления:степень предварительного расширения:

Термический КПД цикла со смешанным подводом тепла будет равен:

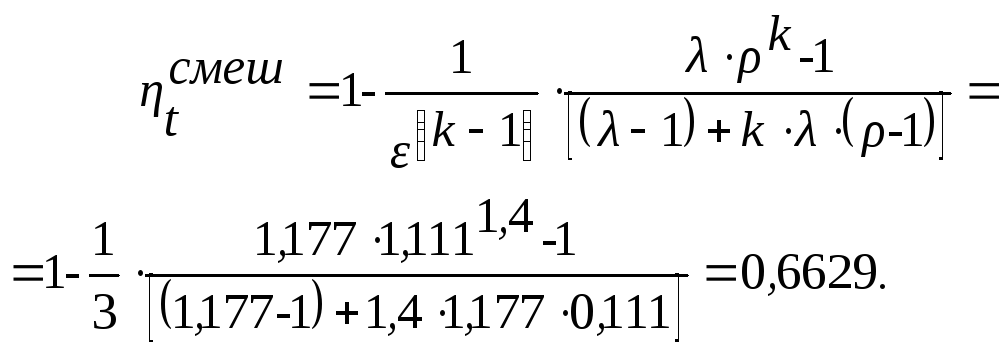
Таким образом, при значениях параметров в исходной точке и одинаковых максимальных параметрах в цикле наибольший термический КПД имеет цикл с изобарным () подводом тепла:

.

3.2 Термический КПД цикла Карно зависит лишь от температур верхнего и нижнего источников теплоты и, следовательно, не зависит от природы рабочего тела. При этом КПД цикла Карнорастет с увеличением температуры верхнего источника и с уменьшением температуры источника теплоты. В случае, если цикл Карно осуществляется в диапазоне температур:

,

его термический коэффициент полезного действия будет равен:

3.3 Рабочее тело (идеальный газ) представляет собой смесь газов, массовый состав которой задан следующим образом – 64%N_2, 14%CO₂, 15%H₂O, 4%H₂, 3%CO.

Газовая постоянная смеси:

Теплоемкости смеси газов:

;

;

При температуре 319⁰К (46⁰С) теплоемкости заданной смеси будут равны:

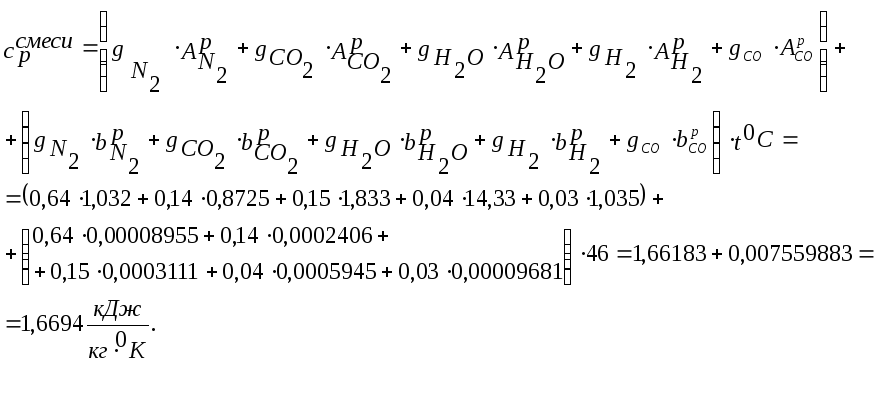
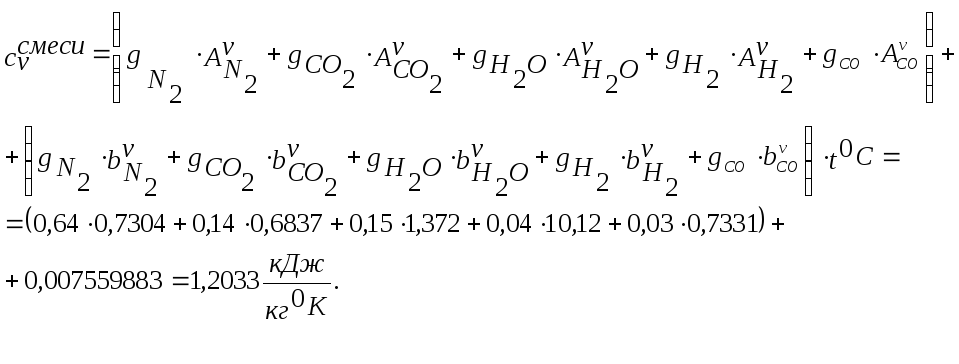
Показатель адиабаты будет равен:

Параметры в характерных точках цикла с газовой смесью.

точка 1: p₁₌0,114МПа, Т₁=319⁰К; из уравнения состояния идеального газа:

точка 2: и тогда из уравнения адиабаты:

Из уравнения состояния идеального газа:

точка 3: Тогда из уравнения состояния:

точка 4: Из уравнения адиабаты:

Из уравнения состояния:

Зная основные термодинамические параметры в характерных точках цикла с газовой смесью (при изобарном подводе тепла), можно определить его характеристики: степень сжатия и степень предварительного расширения.

Точки	Значения термодинамических параметров				Характеристики цикла
	Pi, МПа	vi, м3/кг	Ti,0K	Ti,0C
1	0,114	1,2858	319	9	ε = 15,9925
2	5,337	0,0804	933,69	421,38
3	5,337	0,1114	1293,8	1065	ρ = 1,3856
4	0,1793	1,2858	501,72	419,71

Термический коэффициент полезного действия цикла:

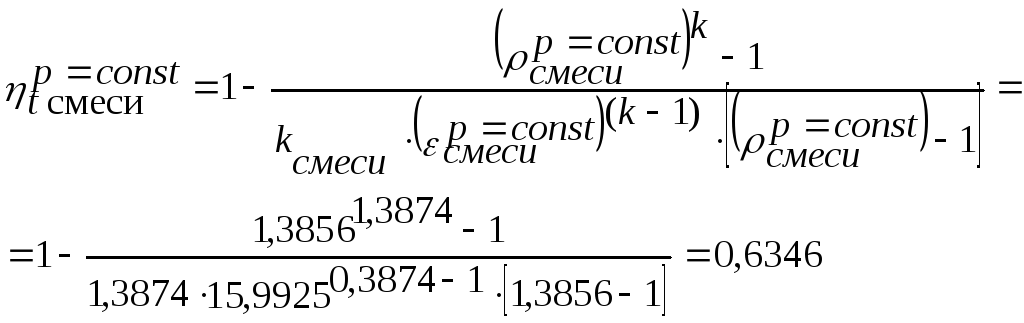
Уменьшение показателя адиабаты приводит к уменьшению термического коэффициента полезного действия цикла:

4. Полный термодинамический анализ всех процессов, из которых состоит цикл с изобарным подводом тепла:

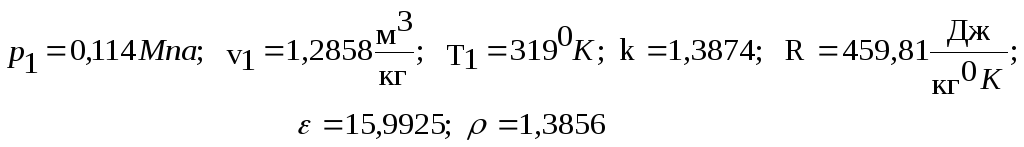
Процесс 1-2 (адиабатное сжатие)

Процесс 2-3 (изобарный подвод тепла)

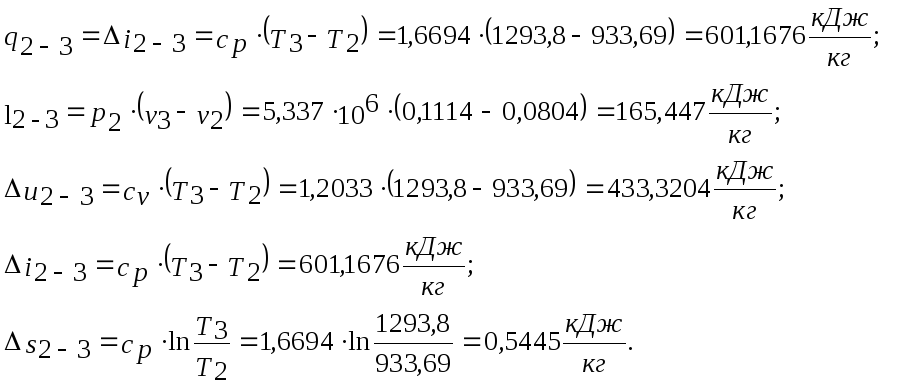
Процесс 3-4 (адиабатное расширение)

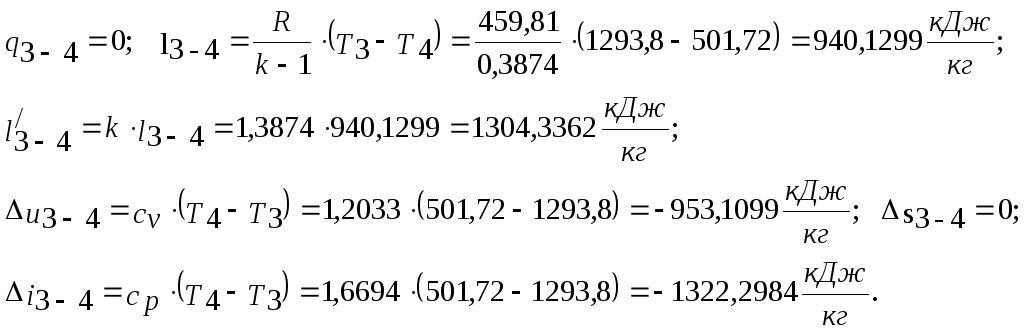
Процесс 4-1 (изохорный отвод тепла)

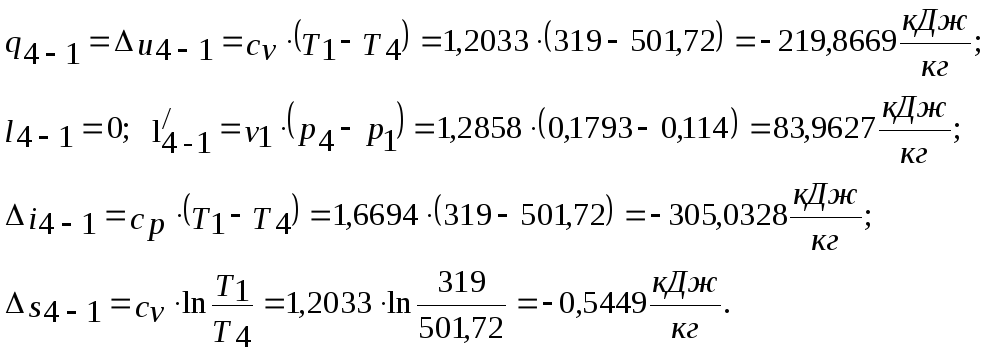
Результаты термодинамического анализа процессов цикла представлены в следующей таблице.

Процесс	q	Δu	Δi	l		Δs
	кДж/кг
1-2	0	739,6565	1026,1635	-729,5834	-1012,224	0
2-3	601,1676	433,3204	601,1676	165,447	0	0.5445
3-4	0	-953,1099	-1322,298	1304,3362	1304,3362	0
4-1	-219,8669	-219,8669	-305,0328	0	83,9627	-0,5449
	381,3007	0.0001	0	740,1998	376.0749	-0,0004

Для цикла, результаты термодинамического анализа которого приведены в таблицах, последнее выражение будет выглядеть следующим образом:

Сравнивая это значение со значением термического КПД получаем значение погрешности определения термического кпд цикла:

Погрешность определения работы цикла:

.