
- •Глава 8 Приложения к экономической теории 153
- •Глава 8. Приложения к экономической теории
- •§8.1 Максимизация выпуска при наличии лимита на ресурсы
- •§8.2 Минимизация издержек при фиксированном объеме выпуска
- •§8.3 Оптимизация потребительского поведения
- •§8.4. Максимизация прибыли в проектном анализе
- •§8.5. Глобальный экстремум в задачах математического программирования
§8.4. Максимизация прибыли в проектном анализе
В процессе принятия инвестиционных решений приходится решать задачу максимизации планируемой прибыли. Одна из функций, с помощью которой в проектном анализе принимается инвестиционное решение (критерий), называется чистым дисконтированным доходом NPV (Net Present Value). Экономический смысл этой функции состоит в максимизации разности между всеми проектными доходами и затратами, т.е. прибыли. Однако, следуя теории проектного анализа, в этом расчете необходимо учесть время произведения затрат и получения доходов, а также процентную ставку. Все это находит отражение в критерии NPV через применение теории изменения ценности денег во времени.
Кладя деньги в банк, мы рассчитываем на денежный прирост. Он определяется по формуле сложных процентов
![]() ,
,
где
![]() - первоначальный вклад, положенный в
банк на
- первоначальный вклад, положенный в
банк на
![]() лет под
лет под
![]() годовых процентов. Поставим теперь
задачу так. Какую сумму надо положить
в банк под
годовых процентов. Поставим теперь
задачу так. Какую сумму надо положить
в банк под
![]() в год, чтобы через
лет получить
в год, чтобы через
лет получить
![]() денежных единиц? Другими словами, найти
стоимость суммы денег, полученной через
лет, но приведенной к настоящему времени.
Очевидно, она равна
денежных единиц? Другими словами, найти
стоимость суммы денег, полученной через
лет, но приведенной к настоящему времени.
Очевидно, она равна
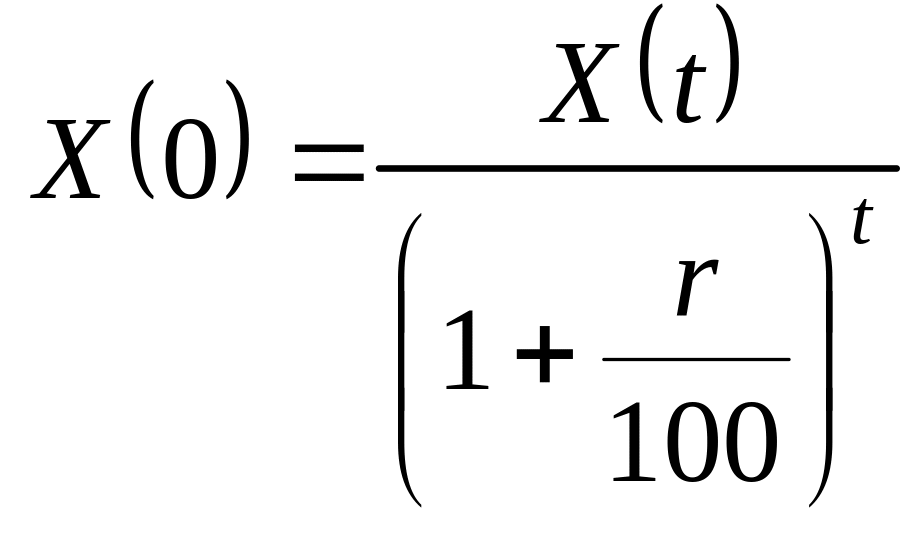 .
.
Величину можно назвать ставкой дисконта1, отражающей изменение стоимости денег во времени.
Предположим, рассчитывается проект,
который принесет через год доход в
размере
![]() денежных единиц, через два года -
денежных единиц, через два года -
![]() денежных единиц и т. д. Тогда пересчитанный
к настоящему времени, он составит в
течение
лет величину, равную
денежных единиц и т. д. Тогда пересчитанный
к настоящему времени, он составит в
течение
лет величину, равную
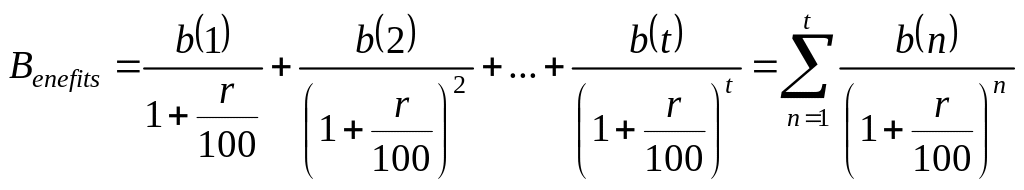 .
.
Реализация проекта потребует затрат в
каждом году жизненного цикла проекта
![]() .
Пересчитанные к настоящему времени,
ежегодные затраты составят величину
.
Пересчитанные к настоящему времени,
ежегодные затраты составят величину
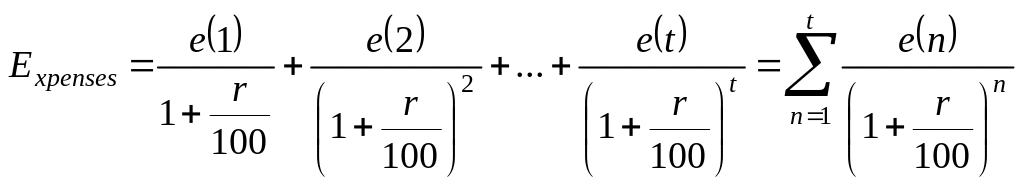 .
.
Рассчитаем чистый дисконтированный
доход NPV (Net
Present Value),
составляющий, как уже указывалось,
разность между приведенными к настоящему
времени будущими потоками доходов и
затрат с учетом инвестиции
![]() в начальный момент. Получим
в начальный момент. Получим
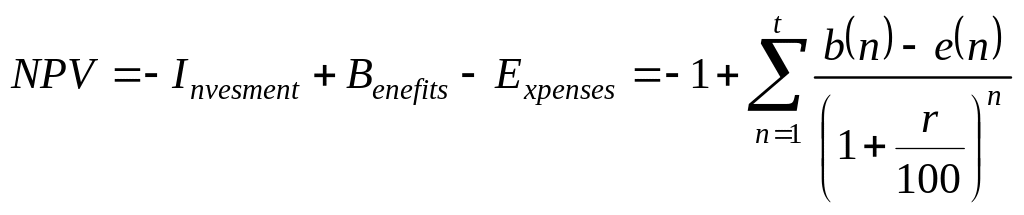 .
.
Чистый дисконтированный доход NPV, как уже говорилось, характеризует эффективность проекта и является одним из основных критериев при выборе проекта. Рассмотрим NPV подробнее. Он представляет собой функцию двух переменных: ставки дисконта и времени жизни проекта (или горизонта его планирования) . Время жизни проекта оказывается конечной величиной, обычно равной 5 – 10 годам, после чего требуется радикальная реорганизация, новое инвестирование или ликвидация проекта. В противном случае проект начнет приносить убытки.
Функция чистого дохода (прибыли)
![]() (доходы минус затраты) для каждого
проекта индивидуальна. Однако некоторые
свойства функции являются общими для
реальных проектов: первоначальный рост,
достижение максимума и последующий
спад.
(доходы минус затраты) для каждого
проекта индивидуальна. Однако некоторые
свойства функции являются общими для
реальных проектов: первоначальный рост,
достижение максимума и последующий
спад.
Конкретизируем немного проект. Пусть проект рассчитан на 10 лет. Рассмотрим два различных случая, отличающиеся различным поведением на заключительной стадии проекта.
1. В начале стадии убывания чистого дохода менеджеры поддерживают проект различными мерами, добиваясь превышения доходов над затратами. Пусть функция прибыли имеет вид (рис. 8.21.)
![]()
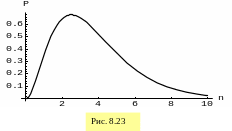 .
.
В начале проекта прибыль растет медленно, в течение трех лет выходит на максимум. Затем в течение последующих 7 лет она падает по экспоненте до 10% от своей максимальной величины.
Зависимость функции NPV
от ставки дисконта
в пределах
![]() и времени развития проекта
по годам приведена на рис. 8.22. Плоскость
на рисунке проведена на уровне
и времени развития проекта
по годам приведена на рис. 8.22. Плоскость
на рисунке проведена на уровне
![]() и отсекает участки с
и отсекает участки с
![]() .
Для каждого года проекта можно определить
величину
(норму
дисконта
.
Для каждого года проекта можно определить
величину
(норму
дисконта
![]() ),
при которой затраты на проект окупятся.
Для
),
при которой затраты на проект окупятся.
Для
![]() это произойдет только в конце проекта
(
это произойдет только в конце проекта
(![]() станет больше нуля). При
станет больше нуля). При
![]() проект станет убыточным. На рис. 8.22.
красная линия отсекает ставку процента
.
Если ставка процента равна, например,
27%, проект окупится к четвертому году
(дисконтированный период окупаемости
- критерий
проект станет убыточным. На рис. 8.22.
красная линия отсекает ставку процента
.
Если ставка процента равна, например,
27%, проект окупится к четвертому году
(дисконтированный период окупаемости
- критерий![]() ).
Белой стрелкой на рис. 8.23 указана точка
на поверхности, соответствующая
).
Белой стрелкой на рис. 8.23 указана точка
на поверхности, соответствующая
![]() и
.
и
.
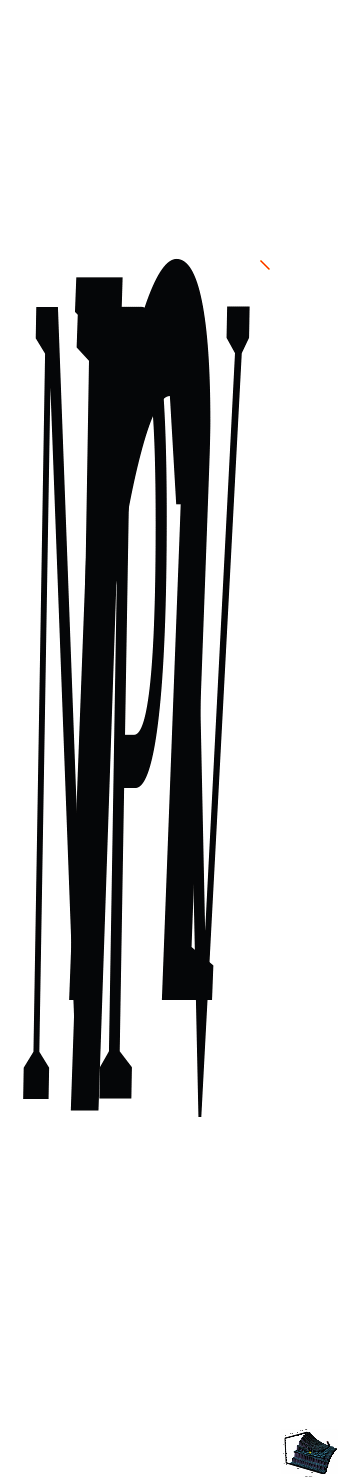
2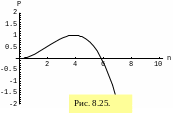 .
Проект не поддерживается новыми идеями,
инвестициями, живет за счет внутренних
ресурсов. Вся прибыль извлекается из
проекта. Или в проекте обнаружились
проблемы, которые привели во второй
половине жизненного цикла проекта к
превышению расходов над доходами Пусть
в этом случае функция прибыли имеет вид
(рис. 8.25.)
.
Проект не поддерживается новыми идеями,
инвестициями, живет за счет внутренних
ресурсов. Вся прибыль извлекается из
проекта. Или в проекте обнаружились
проблемы, которые привели во второй
половине жизненного цикла проекта к
превышению расходов над доходами Пусть
в этом случае функция прибыли имеет вид
(рис. 8.25.)
![]() .
.
В начале проекта прибыль растет медленно, в течение четырех лет она выходит на максимум. Затем в течение последующих двух лет прибыль падает до нуля. Расходы продолжают расти.
З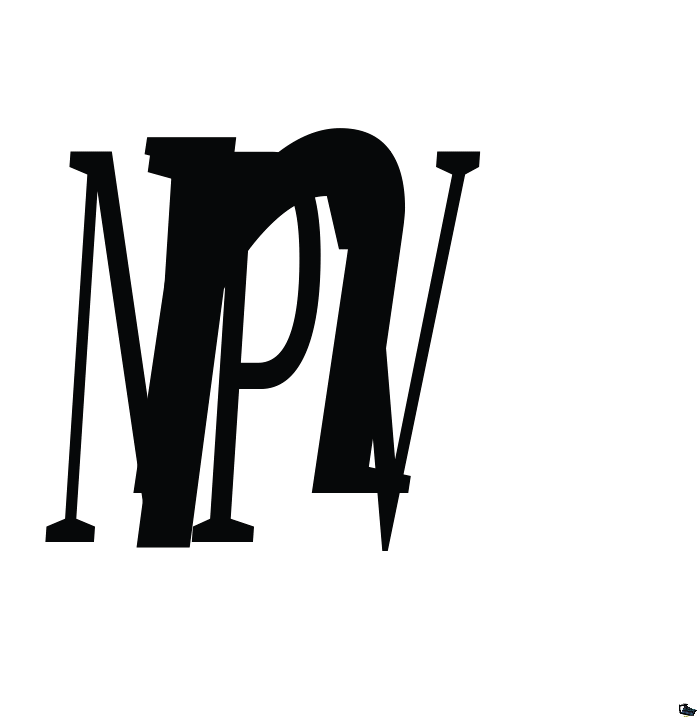
 ависимость
в этом случае функции NPV
от ставки дисконта
в пределах
и времени развития проекта
по годам приведена на рис. 7.26.
По-прежнему, плоскость на рисунке
проходит через ординату со значением
.
В первые годы проект развивается
благополучно. При невысокой ставке
процента прибыль появляется на четвертом
году реализации и достигает на 5-6 годах
максимальных значений. Однако последние
три года могут развиться катастрофические
события. Что на первый взгляд удивительно,
катастрофа возникает при малых ставках
дисконта, в то время как при больших
ставках проект затухает медленно. Это
видно на рис. 8.27. Причина этого явления
в том, что при низкой процентной ставке
деньги с течением времени остаются
«дорогими». Потери денежных средств
на 7-10 году проекта в настоящем времени
весьма чувствительны. При высокой
ставке процента деньги на 7-10 году проекта
становятся «дешевыми». Их потеря не
столь чувствительна.
ависимость
в этом случае функции NPV
от ставки дисконта
в пределах
и времени развития проекта
по годам приведена на рис. 7.26.
По-прежнему, плоскость на рисунке
проходит через ординату со значением
.
В первые годы проект развивается
благополучно. При невысокой ставке
процента прибыль появляется на четвертом
году реализации и достигает на 5-6 годах
максимальных значений. Однако последние
три года могут развиться катастрофические
события. Что на первый взгляд удивительно,
катастрофа возникает при малых ставках
дисконта, в то время как при больших
ставках проект затухает медленно. Это
видно на рис. 8.27. Причина этого явления
в том, что при низкой процентной ставке
деньги с течением времени остаются
«дорогими». Потери денежных средств
на 7-10 году проекта в настоящем времени
весьма чувствительны. При высокой
ставке процента деньги на 7-10 году проекта
становятся «дешевыми». Их потеря не
столь чувствительна.
Действительно, доход, полученный от проекта на -м году жизненного цикла, пересчитанный к началу проекта, равен
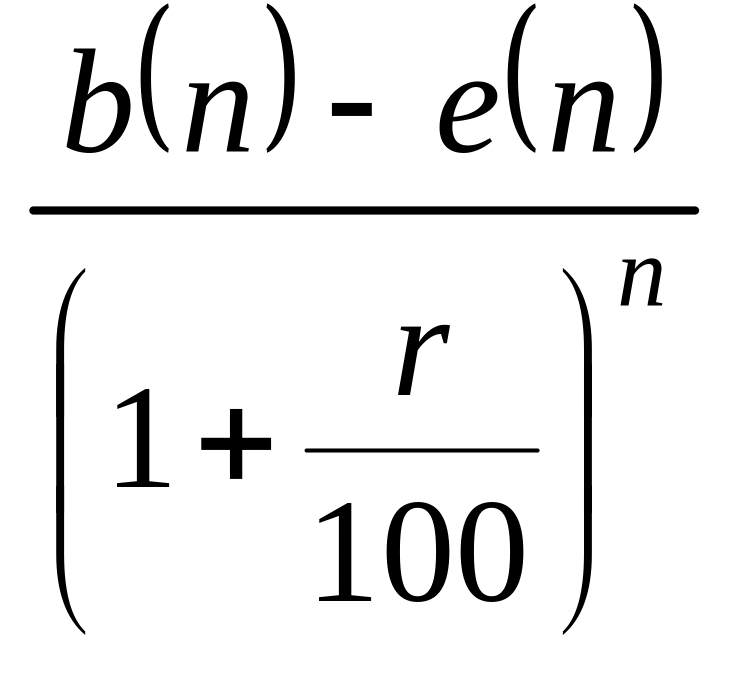 .
.
Отношение прибылей, а в данном случае
убытков при низкой ставке
![]() и высокой ставке
и высокой ставке
![]() составит величину
составит величину
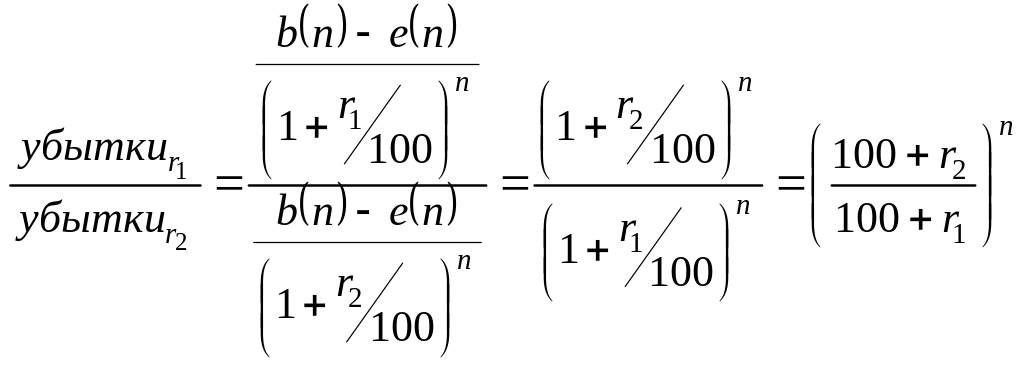 .
.
Для
![]() и
и
![]() на 7-м году жизни проекта будем иметь
на 7-м году жизни проекта будем иметь
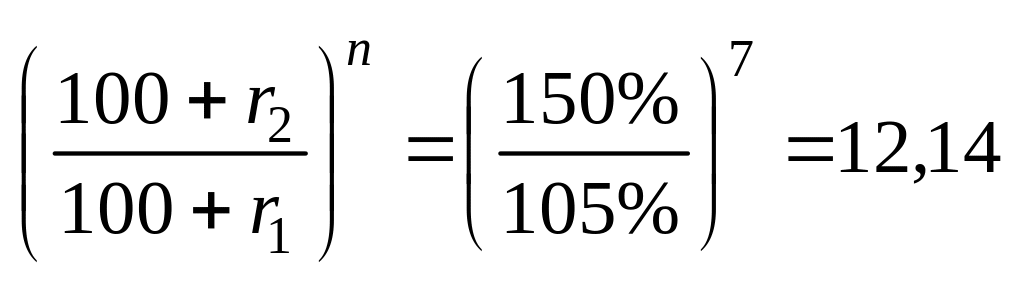 .
.
Это означает, что потери составят при низкой процентной ставке в 12 раз большую величину, чем при высокой. Отсюда вывод: при низкой ставке процента следует более зорко следить за прибылями-убытками. По достижении максимума прибыли и начале спада следует принимать решительные меры, ибо «промедление смерти подобно». Проект при низкой процентной ставке и неблагоприятном стечении обстоятельств может быть потерян для инвестора с большими убытками.
