Глава 8 Приложения к экономической теории 153

Глава 8. Приложения к экономической теории

В этой главе мы решим важные экономические задачи по оптимизации, а также «покачаем» некоторые экзогенные параметры в оптимальной точке. Посмотрим, как будет меняться решение оптимизационных задач.

§8.1 Максимизация выпуска при наличии лимита на ресурсы

Решение в общем виде задачи максимизации выпуска при наличии лимита на ресурсы.

Теоремы о маргинальных значениях (выпуск продукции при вариациях лимита на ресурсы или цены за ресурс).

Решение в общем виде задачи максимизации выпуска при наличии лимита на ресурсы

Пусть производственная функция предприятия, занимающегося выпуском продукции, равна , где - закупаемые по цене – ресурсы, – денежный лимит на закупки. Потребуем выполнения условий: -дважды непрерывно дифференцируемая функция, Решается задача на условный экстремум

Составим функцию Лагранжа

Необходимые условия существования экстремума

Перенеся вторые слагаемые направо и разделив одно равенство на другое, найдем

.

Выразим из уравнения переменную и подставим в уравнение связи

,

что позволяет найти критическое значение переменной . Аналогично находим .

Рассмотрим достаточные условия экстремума

Окаймленный гессиан имеет вид

Условие максимума функции Лагранжа приводит к неравенству

Левая часть неравенства есть квадратичная форма относительно переменных

Выделим матрицу квадратичной формы

Квадратичная форма является положительно определенной, если все угловые миноры ее матрицы положительны

Эти неравенства с учетом следствия из них , записанные в виде системы

задают достаточные условия существования локального максимума функции Лагранжа и условного максимума производственной функции.

Более подробное исследование на экстремум (например, случай нестрогого максимума) требует применения главных миноров и приводит к появлению знаков равенства в достаточных условиях. Детальный учет области определения задачи приводит к дополнительным ограничениям на производственную функцию, в частности,

ПРИМЕР. Каким условиям должна удовлетворять функция Кобба-Дугласа , как производственная функция, для которой выполняются достаточные условия максимума, если ?

Решение. Найдем вторые производные и запишем для них достаточные условия

Перейдем к системе неравенств для коэффициентов

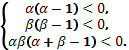
Решение системы неравенств дает интервалы изменения α и β:

Замечание. При рассмотрении задачи на нестрогий максимум в системе дополнительно появляются знаки равенства.

Теоремы о маргинальных значениях

(выпуск продукции при вариациях лимита на ресурсы или цены за ресурс).

Величины задают критическую точку, положение которой зависит от параметров задачи Изменение параметров приводит к вариациям максимума производственной функции . Поэтому величины могут рассматриваться как функции переменных :

- функция условного спроса на 1-й ресурс,

- функция условного спроса на 2-й ресурс со стороны предприятия на рынке.

Подставим в исследуемую производственную функцию и в уравнение связи, предварительно убрав для удобства верхние индексы

Второе уравнение связывает две функции и три аргумента Будем опираться на эту систему при выводе некоторых важных утверждений экономической теории.

1. Продифференцируем оба равенства системы по и воспользуемся необходимыми условиями и :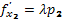

Следовательно, предельное предложение по лимиту равно множителю Лагранжа . Поясним это детальнее.

Поскольку , то 1-е уравнение системы можно записать так

.

Если предприятие оптимизировало выпуск продукции, то дальнейшее увеличение выпуска пропорционально увеличению затрат на сырье с коэффициентом пропорциональности .

Следствие. Используя необходимые условия , где а также найденное выражение для предложения по лимиту , можем записать

.

Отношение предельной полезности ресурса к цене за ресурс равно предельному предложению по лимиту и не зависит от вида ресурса.

2. Продифференцируем оба равенства системы по и используем необходимые условия

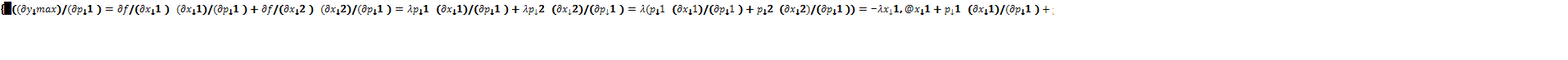
Итак, . Отсюда следует, что предельное предложение по цене за 1-й ресурс пропорционально объему ресурса. Дадим пояснение. Заменим на . Тогда

.

Предприятие, работающее в оптимальном режиме, уменьшит выпуск продукции пропорционально как увеличению цены на ресурс, так и объему закупаемого ресурса.

Вариации выпуска продукции при изменении цены на 2-й ресурс находятся аналогично.

Следствие. Найдем λ из необходимых условий и формулы предельного предложения по цене и приравняем выражения. Из равенства легко получить

Отношение предельной полезности ресурса к предельной полезности денег за ресурс равно цене единицы этого ресурса, взятой со знаком минус, и не зависит от вида ресурса.

Обоснованные в параграфе зависимости вариаций максимального выпуска продукции от параметров задачи получили название теорем о маргинальных значениях.