
§1.4. Обратная матрица
Теорема о существовании обратной матрицы Свойства обратных матриц Ортогональная матрица Симметричная матрица |
Теорема о существовании обратной матрицы
Матрица
называется невырожденной, если ее
определитель отличен от нуля, т.е.
![]() В противном случае она называется
вырожденной.
В противном случае она называется
вырожденной.
Определение. Матрица
![]() называется обратной по отношению
к квадратной матрице
,
если выполняется равенство
называется обратной по отношению
к квадратной матрице
,
если выполняется равенство
![]() . (8)
. (8)
Следующая теорема устанавливает условия существования обратной матрицы.
(о существовании обратной матрицы)
Обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденна.
◄Необходимость. Пусть матрица
имеет обратную матрицу
.
Тогда
.
Используя свойство 11 определителя,
получаем
![]() ,
откуда вытекает
,
откуда вытекает
![]() .
Следовательно,
.
Следовательно,
![]() .
Матрица
является невырожденной.►
.
Матрица
является невырожденной.►
◄Достаточность. Пусть матрица
является невырожденной:
.
Матрицу
транспонируем и на основе транспонированной
матрицы
построим новую матрицу
![]() ,
элементами которой являются алгебраические
дополнения элементов матрицы
.
Назовем эту матрицу
присоединенной. Итак
,
элементами которой являются алгебраические
дополнения элементов матрицы
.
Назовем эту матрицу
присоединенной. Итак
 .
.
Найдем новую матрицу
как произведение матриц
и
:
![]() .
Она имеет вид
.
Она имеет вид
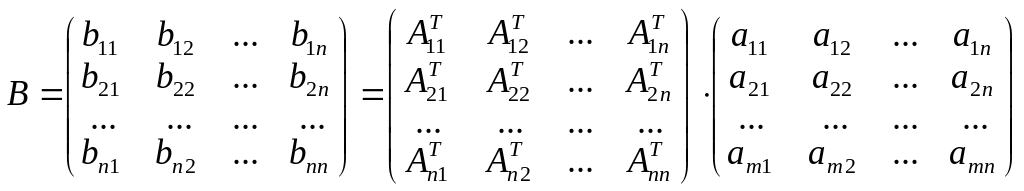 .
.
Элементы матрицы
вычислим по отдельности и воспользуемся
равенством
![]() ,
которое легко проверяется.
,
которое легко проверяется.
![]() .
.
![]() .
.
………………………………………………………………………..……….
Продолжая вычисления дальше, обратим внимание на то, что отличными от нуля окажутся только диагональные элементы матрицы :
![]()
Поэтому матрица имеет вид
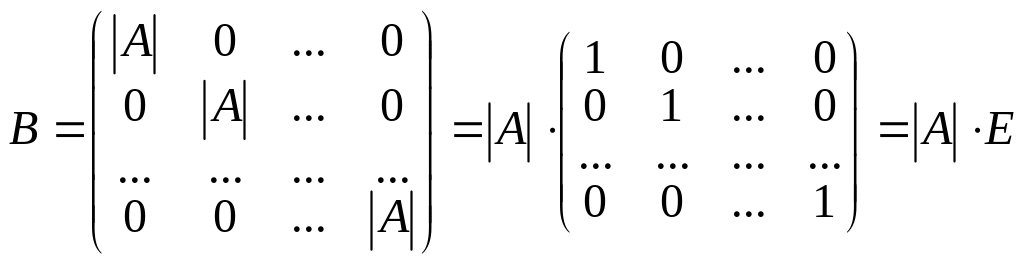 .
.
Следовательно, ![]() .
.
Аналогично можно доказать, что ![]() .
.
Рассмотрим соотношение ![]() .
.
Разделив его на
,
получим ![]() .
.
Поскольку для матрицы
![]() выполнено равенство (8), эта матрица
является обратной по определению
выполнено равенство (8), эта матрица
является обратной по определению ![]() .►
.►
Единственность обратной матрицы. ◄Пусть
кроме обратной матрицы
к матрице
существует еще одна обратная матрица
![]() .
Тогда выполняется равенство
.
Тогда выполняется равенство
![]() .
Умножим это равенство справа на
.
Получим
.
Умножим это равенство справа на
.
Получим
![]() ,
откуда
,
откуда
![]() или
или
![]() .
Таким образом, не существует обратной
матрицы
.
Таким образом, не существует обратной
матрицы
![]() ,
отличной от
.
Аналогично доказывается, что равенство
,
отличной от
.
Аналогично доказывается, что равенство
![]() выполняется в том единственном случае,
когда
выполняется в том единственном случае,
когда
![]() .►
.►
Свойства обратных матриц
1)
![]() .
.
◄Умножим обе части равенства слева на .
![]() .
.
Слева стоит произведение матрицы
на обратную ей
![]() ,
которое равно единичной матрице, справа
произведение обратной матрицы на
исходную, также равное единичной
матрице. Следовательно, равенство
верно.►
,
которое равно единичной матрице, справа
произведение обратной матрицы на
исходную, также равное единичной
матрице. Следовательно, равенство
верно.►
2)
![]() .
.
◄Умножим обе части равенства слева на :
![]() .
.
Далее воспользуемся 4-м свойством
транспонирования матрицы и перепишем
левую часть соотношения так:
![]() .
Правая часть равенства есть произведение
матрицы
на обратную ей. Получаем
.
Правая часть равенства есть произведение
матрицы
на обратную ей. Получаем
![]() .
Откуда следует тождество
.
Откуда следует тождество
![]() .►
.►
3)
![]() .
.
◄Умножим слева равенство на
![]() .
.
![]() .
.
Левую часть равенства представим в
виде произведения
![]() сомножителей
сомножителей
![]() .
.
Левая часть равенства свертывается до матрицы , правая часть равенства есть произведение матрицы на обратную ей. Следовательно, равенство обращается в тождество .►
4) .
◄Для равенства
![]() воспользуемся свойством 11 определителей.
Получим
воспользуемся свойством 11 определителей.
Получим![]() ,
откуда следует
,
откуда следует
![]() .
Поэтому
.►
.
Поэтому
.►
5)
![]()
◄Умножим равенство слева на матрицу .
![]() .
.
Правая часть соотношения примет вид
![]() или
.
Итак
или
.
Итак
![]() .
.
Умножим последнее равенство слева на . Получим
![]() .
.
Слева стоит произведение матрицы
![]() на
обратную ей
на
обратную ей
![]() ,
справа - произведение матрицы
на обратную ей
.
Следовательно,
.
Свойство 5 доказано.
►
,
справа - произведение матрицы
на обратную ей
.
Следовательно,
.
Свойство 5 доказано.
►
Доказанная теорема дает способ вычисления обратной матрицы.
ПРИМЕР. Найти матрицу, обратную данной
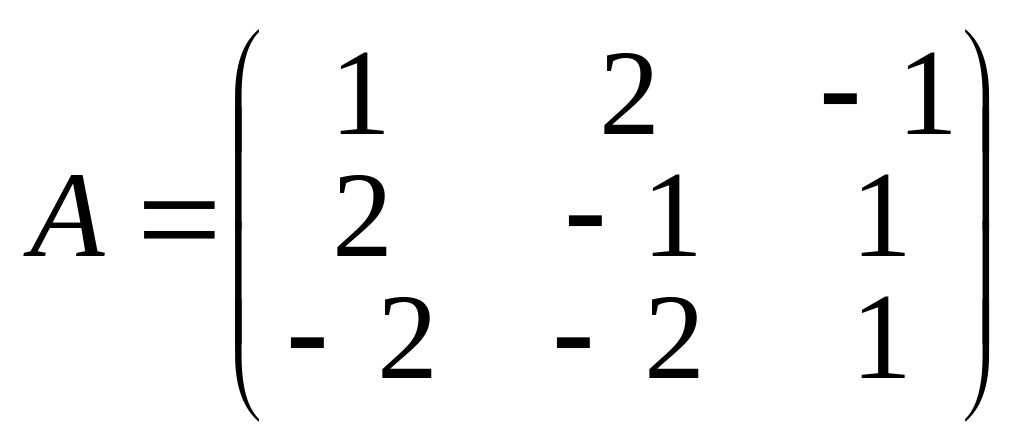 .
.
Решение. Обратную матрицу будем искать, делая последовательно следующие шаги:
1) Находим
определитель матрицы
.
Его величина
![]() .
Следовательно, обратная матрица
существует.
.
Следовательно, обратная матрица
существует.
2) Находим транспонированную к матрицу
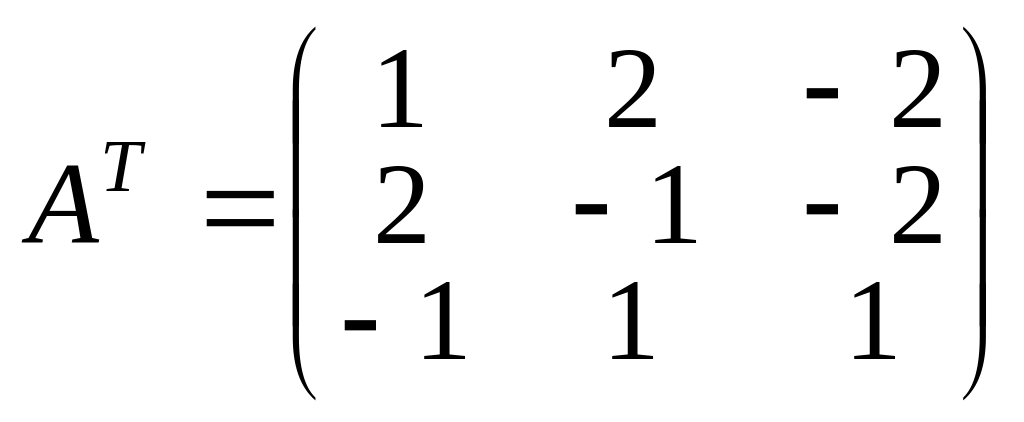 .
.
3) Находим алгебраические дополнения к элементам матрицы
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Выписываем присоединенную матрицу:
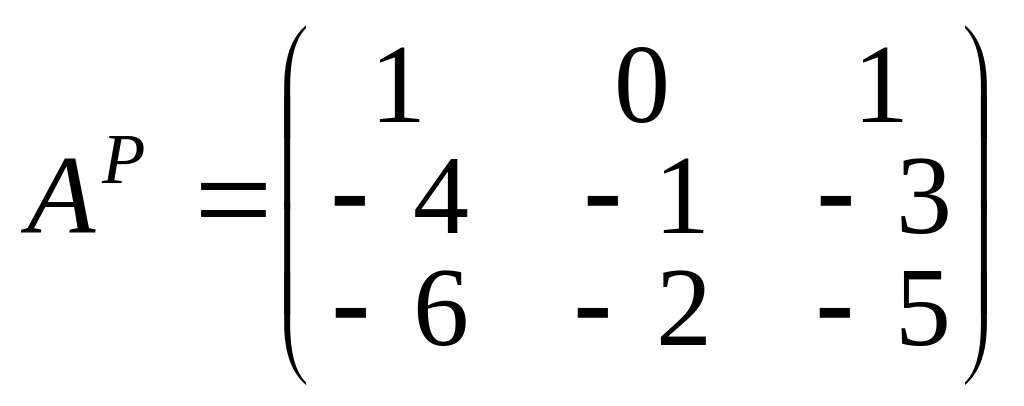 .
.
4) Вычисляем обратную матрицу:
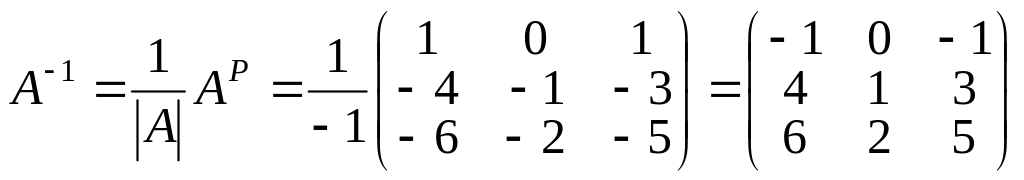 .
.
Другой способ вычисления обратной матрицы дает метод Жордана. Но вначале познакомимся с ортогональной матрицей, с симметричной матрицей и с матрицами элементарных преобразований, на использовании которых основан этот метод.
Ортогональная матрица
Матрица ![]() называется ортогональной, если
называется ортогональной, если ![]() .
.
Из определения следуют следующие свойства.
 – квадратная матрица.
– квадратная матрица.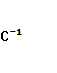 -
ортогональная матрица.
-
ортогональная матрица.
Если
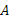 и
и 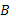 ортогональные матрицы и
ортогональные матрицы и 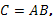 то
является ортогональной матрицей.
то
является ортогональной матрицей.Матрица
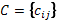 ортогональна тогда и только тогда,
когда
ортогональна тогда и только тогда,
когда
![]() и
и ![]() .
.
Симметричная (симметрическая) матрица
Матрица
называется симметричной, если ![]() .
.
Перечислим некоторые свойства симметричной матрицы
Если симметричная матрица имеет обратную, то она инволютивна, т.е.
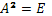 ,
и ортогональна.
,
и ортогональна.Если матрица симметрична и имеет обратную, то она ортогональна и инволютивна.
