Глава 1. Матричная алгебра
§1.1. Матрицы
Основные сведения о матрицах Виды матриц |
Матричная алгебра играет большую роль в экономических расчетах. Многие экономико-математические модели рассматриваются и решаются в матричной форме.
Основные сведения о матрицах
Определение. Матрицей с размерами
![]() называется прямоугольная таблица чисел,
содержащая
называется прямоугольная таблица чисел,
содержащая
![]() строк и
строк и
![]() столбцов. Числа, составляющие матрицу,
называются элементами матрицы. Матрицы
обычно обозначаются заглавными буквами
латинского алфавита, например, А, В,
С,..., а для обозначения элементов
матрицы используются строчные буквы с
двойной индексацией:
столбцов. Числа, составляющие матрицу,
называются элементами матрицы. Матрицы
обычно обозначаются заглавными буквами
латинского алфавита, например, А, В,
С,..., а для обозначения элементов
матрицы используются строчные буквы с
двойной индексацией:
![]() ,
где
,
где
![]() -
номер строки,
-
номер строки,
![]() -номер
столбца. Числа
и
определяют расположение элемента
в матрице
-номер
столбца. Числа
и
определяют расположение элемента
в матрице
![]() и играют роль координат этого элемента
в прямоугольной таблице чисел.
и играют роль координат этого элемента
в прямоугольной таблице чисел.
Например, матрица

имеет строк и столбцов.
Набор
![]()
называется -й строкой матрицы , а набор
![]()
называется -м столбцом матрицы . Любые строки и столбцы матрицы , в свою очередь являются матрицами.
Две матрицы А и В одинаковых
размеров называются равными, если
они совпадают поэлементно. Равенство
записывается как
![]() .
.
Виды матриц
Матрица произвольных размеров, все
элементы которой равны нулю, называется
нулевой и обозначается
![]() .
.
Матрица, состоящая из одной строки
![]() ,
называется матрицей-строкой, или
вектором.
,
называется матрицей-строкой, или
вектором.
Матрица, состоящая из одного столбца
 ,
называется матрицей-столбцом или также
вектором.
,
называется матрицей-столбцом или также
вектором.
Матрица называется квадратной -го порядка, если число ее строк равно числу столбцов и равно .
Элементы квадратной матрицы , у которых номер строки совпадает с номером столбца, называются диагональными и образуют главную диагональ.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
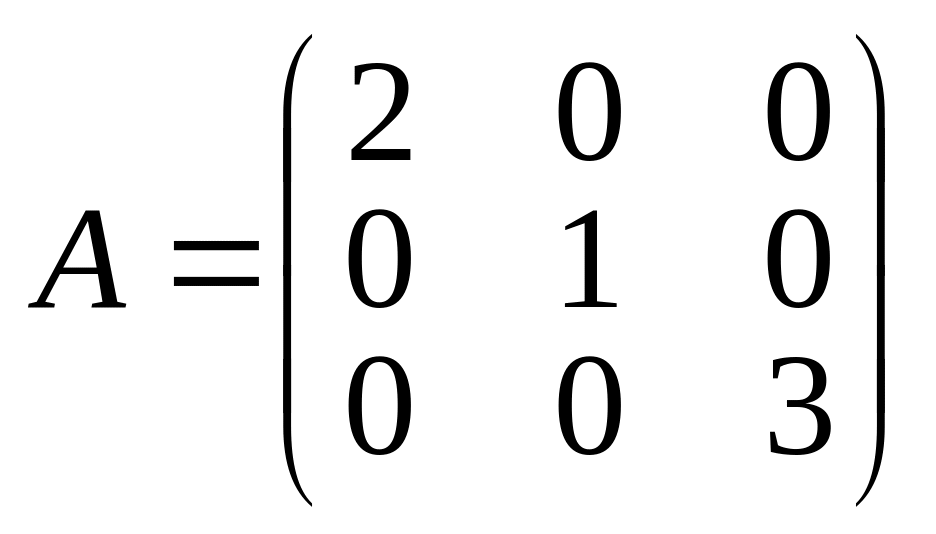
-диагональная матрица третьего порядка.
Квадратная матрица, на главной диагонали
которой стоят единицы, а все остальные
элементы равны нулю, называется единичной
и обозначается
![]() .
Например, матрица
.
Например, матрица

является единичной матрицей 4-го порядка.
Квадратная матрица, у которой все элементы выше или ниже главной диагонали равны нулю, называется треугольной.
Произвольная матрица вида
![]() ,
составленная из двух матриц, разделенных
вертикальной чертой, называется
расширенной. Например, матрица
,
составленная из двух матриц, разделенных
вертикальной чертой, называется
расширенной. Например, матрица
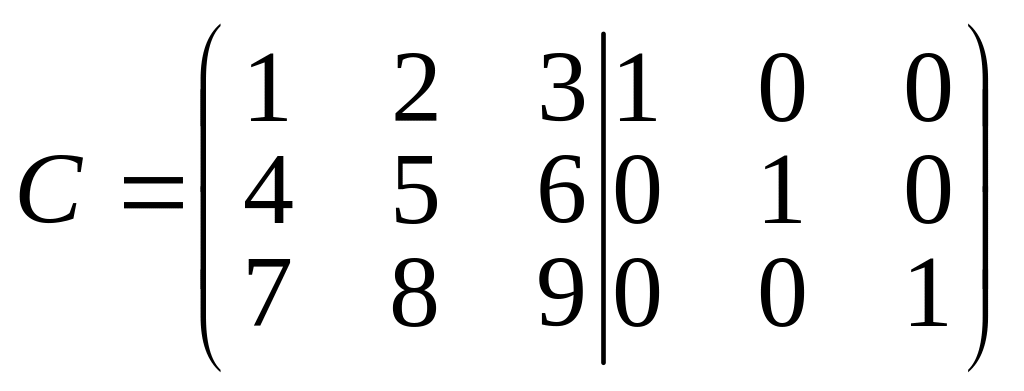
является расширенной. Она составлена из квадратной матрицы 3-го порядка и единичной матрицы 3-го порядка.
Матрица может содержать своими элементами другие матрицы. Например, матрица
может быть записана в виде
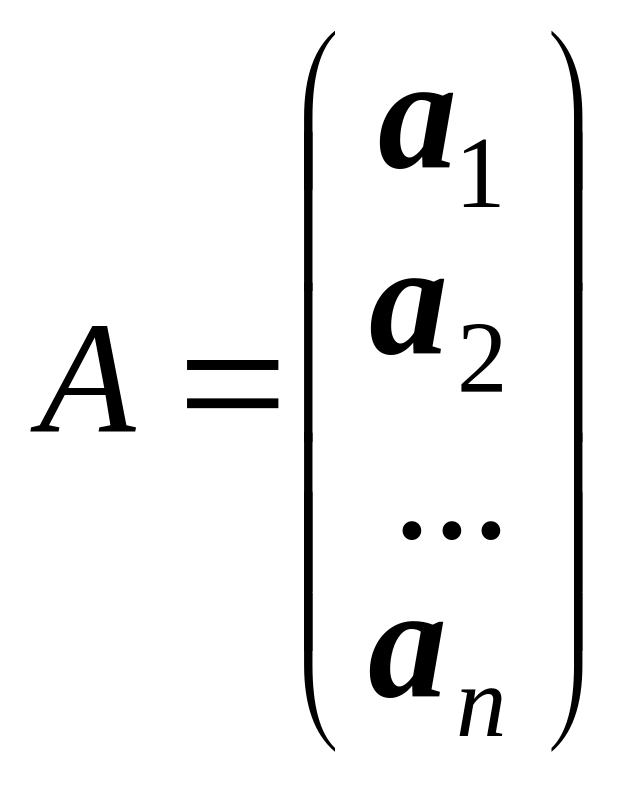 ,
где
,
где
![]() - матрицы-строки исходной матрицы.
- матрицы-строки исходной матрицы.
§1.2. Операции над матрицами
Умножение числа на матрицу Сложение матриц одинаковых размеров Вычитание матриц одинаковых размеров Умножение матрицы на матрицу Возведение матрицы в целую положительную степень Транспонирование матрицы Свойства транспонирования |
Над матрицами возможно проведение некоторых арифметических операций.
1) Умножение числа на матрицу
( производится по следующему правилу: число умножается на каждый элемент матрицы ).
Произведением числа
![]() на матрицу
на матрицу
![]() называется матрица
называется матрица
![]() такая, что
такая, что
![]() .
Элементы матрицы
.
Элементы матрицы
![]() вычисляются по формуле
вычисляются по формуле
![]() ,
где
,
где
![]() .
.
Замечание. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
2) Сложение матриц одинаковых размеров
( соответствующие элементы матриц складываются ).
Суммой матриц
и
![]() называется матрица
называется матрица
![]() такая, что
такая, что
![]() .
Элементы матрицы
.
Элементы матрицы
![]() вычисляются по формуле
вычисляются по формуле
![]() ,
где
.
,
где
.
3) Вычитание матриц одинаковых размеров
( соответствующие элементы матриц вычитаются ).
Разностью матриц
и
называется матрица
такая, что
![]() .
Элементы матрицы
вычисляются по формуле
.
Элементы матрицы
вычисляются по формуле
![]() ,
где
.
,
где
.
4) Умножение матрицы на матрицу
( элемент новой матрицы, стоящий на пересечении i-й строки и j-го столбца равен сумме произведений элементов i-ой строки первой матрицы на соответствующие элементы j-го столбца второй матрицы. Операция определена при условии, что число столбцов 1-й матрицы равно числу строк 2-й )
Произведением матрицы
на матрицу
называется матрица
такая, что
![]() .
Элементы матрицы
вычисляются по формуле
.
Элементы матрицы
вычисляются по формуле
![]() . (1)
. (1)
ПРИМЕР.
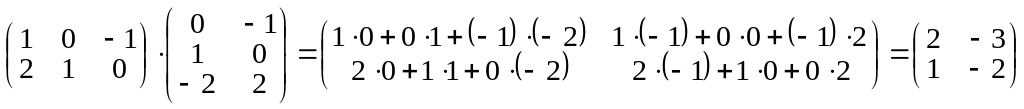 .
.
Замечание 1. Используя знак сокращенного суммирования, формулу (1) можно записать в виде
![]() .
.
Замечание 2. Введем обозначение матрицы
в виде
![]() ,
означающее, что матрица содержит
строк и
столбцов. Тогда произведение матриц
можно записать следующим образом:
,
означающее, что матрица содержит
строк и
столбцов. Тогда произведение матриц
можно записать следующим образом:
![]()
Замечание 3. Порядок матриц-сомножителей существен. Поэтому говорят об умножении матрицы на матрицу справа или слева.
Если произведение матриц
![]() существует, то произведение матриц
существует, то произведение матриц
![]() может не существовать.
может не существовать.
Если существуют произведения матриц и , они могут быть матрицами разных размеров.
Если матрицы
и
квадратные, то их произведения
и
существуют и имеют одинаковый порядок,
но в общем случае
![]() .
.
Замечание 4. Умножение единичной матрицы
на
квадратную матрицу
не изменяет последней:
![]() .
.
Замечание 5. Произведение двух ненулевых матриц может дать нулевую матрицу , например
![]()
5) Возведение матрицы в целую положительную степень
Возведение матрицы в целую положительную
степень
![]() сводится
к произведению
одинаковых
матриц:
сводится
к произведению
одинаковых
матриц:
![]() .
.
Дополнительно определим
![]() .
.
Замечание 1. Возведение в степень матрицы может привести к нулевой матрице. Например,
![]() .
.
Замечание 2. Операция возведения в степень определена только для квадратных матриц.
6) Транспонирование матрицы
( переход к матрице, у которой строки и столбцы меняются местами ).
Матрица

называется транспонированной по отношению к матрице
и обозначается
![]() .
.
Замечание. Из определения следует, что
если матрица А имеет размеры
,
то транспонированная матрица
имеет размеры
![]() .
.
Операции транспонирования, а также операции сложения и умножения матриц обладают легко проверяемыми свойствами.
Свойства транспонирования
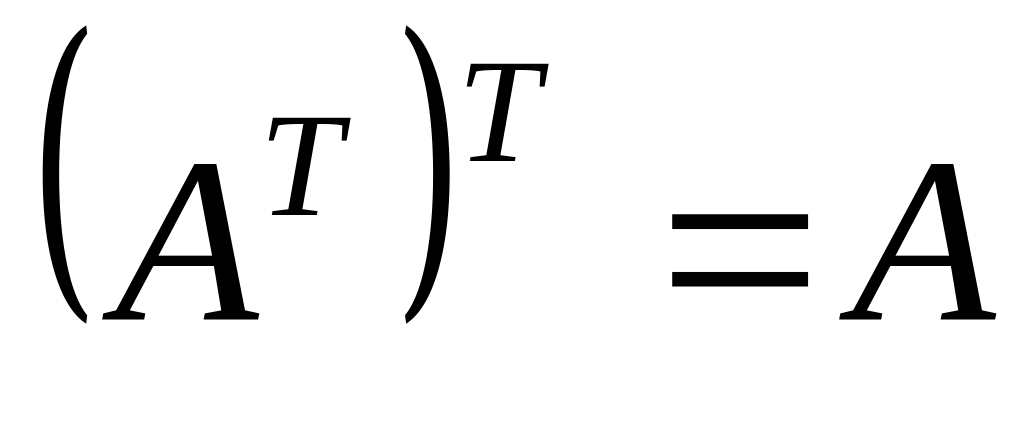
 ,
где
,
где
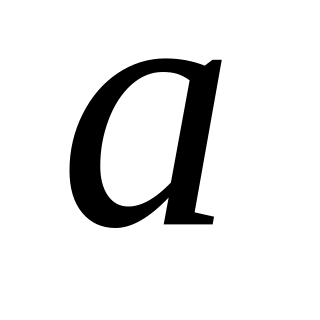 -
число.
-
число.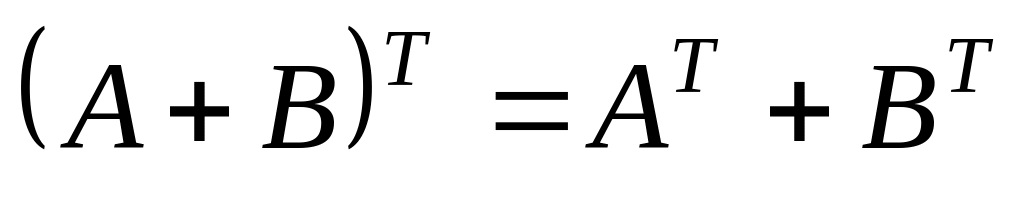

Свойства операций сложения и умножения.
А+В=В+А
(А+В)+С=А+(В+С)
 (А+В)=
А+
В
(А+В)=
А+
ВA(В+С)=AB+AC
(А+В)С= АС+ВС
С(АВ)= (СА)В