
- •Выборочное наблюдение
- •Способы формирования выборочной совокупности.
- •Символы основных характеристик параметров генеральной и выборочной совокупностей
- •I. Простая случайная выборка
- •Средние и предельные ошибки выборки
- •Ошибка выборочной доли.
- •II. Механическая выборка
- •III. Типическая выборка
- •III. Серийная выборка
- •При повторном отборе средняя ошибка выборки вычисляется:
- •Определение необходимой численности выборки
II. Механическая выборка
Применяется, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера, номера домов, квартир).
Для проведения механической выборки устанавливается пропорция отбора. Например, для совокупности в 500000 единиц предполагается получить 2% выборку, то пропорция отбора составит 1/50, а для 5% выборки – 1/20.
Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы. При пропорции 1/ 50 отбирается каждая 50-я единица. Однако такой отбор выбирает единицу начала интервала, или конца интервала, т.е. крайнюю, что ведет к накоплению систематической ошибки. Поэтому целесообразно начинать отбор с середины первого интервала. Например. при 5% выборке отобрать 10-ю, 30-ю,50-ю и прочие единицы с таким же интервалом.
Средняя ошибка выборки, необходимый объем выборки, т.е. все показатели выборочной совокупности рассчитываются как и при собственно-случайной выборке.
III. Типическая выборка
При типическом (районированном) отборе генеральная совокупность разбивается на однородные типические группы, районы. Отбор единиц наблюдения в выборочную совокупность производится различными методами.
1. Рассмотрим типическую выборку с пропорциональным отбором внутри типических групп. Объем выборки из типической группы при отборе, пропорциональном численности типических групп, определяется по формуле:
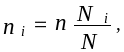
где
![]() объем
выборки из
объем
выборки из
![]() типической группы;
типической группы;
![]() общий
объем выборки,
общий
объем выборки,
![]() объем
типической группы,
объем
типической группы,
![]() объем
генеральной совокупности.
объем
генеральной совокупности.
Предельная ошибка выборочной средней и доли при бесповторном случайном и механическом отборе внутри типических групп рассчитывается по формулам

При повторном отборе
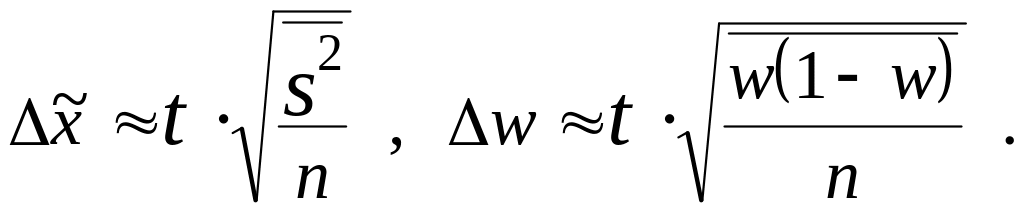
При
этом общая выборочная средняя
рассчитывается из групповых выборочных
средних по формуле:
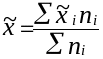 .
.
Средняя
выборочная из внутригрупповых дисперсий:
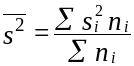
Средняя
выборочная доля рассчитывается по
формуле:
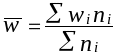
Средняя из внутригрупповых дисперсий доли определяется по формуле:
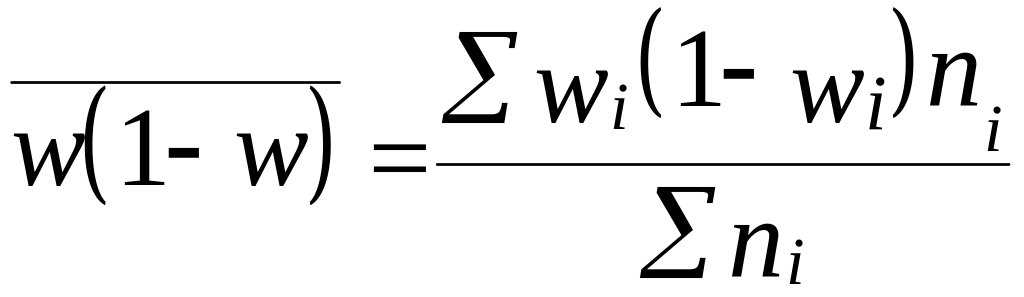
2. Типическая выборка может производиться пропорционально дифференциации признака, при этом число наблюдений в каждой группе рассчитывается с учетом СКО признака в каждой группе. Такой отбор дает лучший результат, но применение его на практике затруднено вследствие трудности получения сведений о вариации до проведения наблюдения.
III. Серийная выборка
При серийном способе отбора генеральную совокупность делят на одинаковые по объему группы- серии. Примерами серий могут быть упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады. В выборочную совокупность отбираются серии путем случайного или механического отбора. Внутри серий производится сплошное наблюдение единиц.
При повторном отборе средняя ошибка выборки вычисляется:

При
бесповторном
отборе серий средняя ошибка выборочной
средней и средняя ошибка выборки для
доли
определяются по формуле: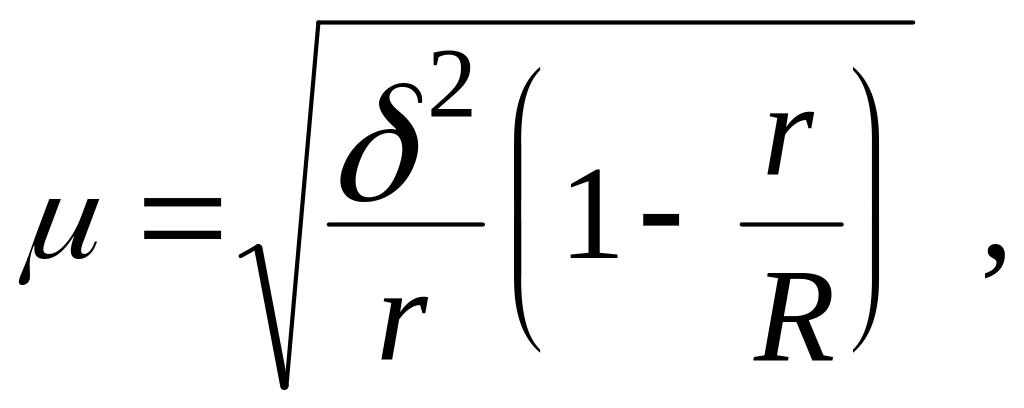
где
![]() -
межсерийная
дисперсия средних
или
межсерийная дисперсия доли,
-
межсерийная
дисперсия средних
или
межсерийная дисперсия доли,
![]() -
число серий в генеральной совокупности,
-
число серий в генеральной совокупности,
![]() -
число отобранных серий.
-
число отобранных серий.
Межсерийная дисперсия вычисляется:
![]()
Где Х - средняя -ой серии,
Х - общая средняя по всей выборочной совокупности.
Пример 3.
