
Дворецкий С.И., Муромцев Ю.Л., Погонин В.А., Схиртладзе А.Г. Компьютерное Моделирование технологических процессов и с
.pdf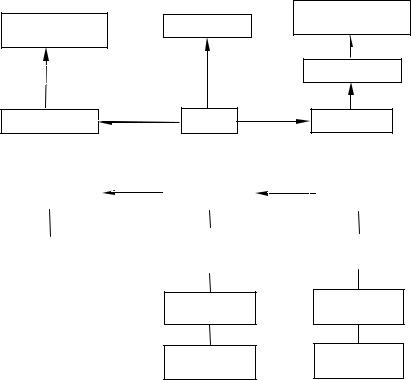
использовать структуру иерархического типа, в которой комбинируются другие виды фреймов.
Важнейшим свойством фреймовых моделей является заимствованное из семантических моделей наследование свойств. Наследование происходит по АКО-связям (A-Kind-Of = это). Слот АКО указывает на фрейм более высокого уровня, откуда неявно наследуется, т.е. переносятся, значения аналогичных слотов.
Аппарат для пере- |
|
|
Термочувствительный |
|
Стабилизация |
элемент |
|
дачи теплоты |
|
|
это |
|
|
|
|
это |
свойство |
Термопара |
|
|
|
|
например |
Теплообменник |
принадлежит |
ЛСУ |
имеет |
Датчик |
|||
|
|
|
частью |
Рис. 5.4. Семантическая сеть
|
|
|
это |
|
|
это |
|
|
|
|
Руководитель |
Мастер |
Сотрудник |
||||||
|
низшего звена |
|
|
|
цеха КИПиА |
|
|
цеха КИПиА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Способности – |
|
|
|
|
|
Умеет организо- |
|
|
|
|
|
Образование – |
|
|
|
|
|
|
хороший орга- |
|
|
|
||
|
вать работу уча- |
|
|
|
|
|
высшее |
|
|
|
|
|
|
низатор |
|
|
|
||
|
стка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возраст –
25 – 60 лет
Любит смотреть футбол
Возраст –
17 – 60 лет
Носит спецодежду
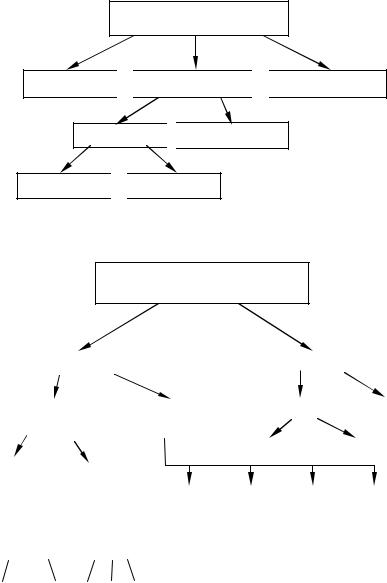
Рис. 5.5. Фреймовая модель
Пример 5.3. Во фреймовой модели на рис. 5.5 понятие «Сотрудник» наследует свойства фреймов «Мастер цеха КИПиА» и «Руководитель низшего звена», которые находятся на более высоком уровне иерархии.
Основой формальных логических моделей является классическое исчисление предикатов 1 порядка, т.е. когда предметная область или задача описывается в виде набора аксиом. Описание этих моделей в данном разделе не приводится, так как исчисление предикатов 1 порядка в промышленных СИИ практически не используется.
5.3. Определение и классификация неопределенности
Современные производства, рассматриваемые с позиций системного подхода, состоят из большого количества взаимосвязанных подсистем, между которыми существуют отношения соподчиненности в виде иерархической структуры.
Управление такой системой является чрезвычайно сложной задачей, решаемой методами математического моделирования с использованием декомпозиционного подхода.
Задача усложняется тем, что технологические процессы характеризуются следующим, достаточно общим, набором факторов: наличием нелинейности; распределенностью параметров в пространстве и времени; нестационарностью; непрерывным дрейфом технологических параметров; не полной наблюдаемостью некоторых величин; часто меняющейся номенклатурой и объемом выпускаемой продукции; колебаниями качества и цен используемого сырья; вербальным уровнем формализации информации, используемой для решения задач управления и принятия решений.
Перечисленные факторы являются причиной, порождающей существенные трудности при решении задач оценки переменных состояния и идентификации объектов, которые лежат в основе построения их адекват-
ного математического описания, используемого при решении задач управления, принятия решений и оптимизации.
Большинство существовавших методов идентификации ориентировано на идеализированные условия работы объектов (полную наблюдаемость, детерминированность физико-химических свойств, отсутствие случайных неконтролируемых помех и др.). При таких допущениях для решения задач управления во многих практических случаях используют детерминированные математические модели.
Последние имеют недостатки, обусловленные невозможностью определения точных значений входящих в них параметров, что определяется влиянием факторов неопределенности.
Под неопределенностью будем понимать случайность параметров и нечеткость констант, относящихся к технологическому процессу или производству, например: теплопереноса (теплофизические характеристики материала, коэффициенты теплоотдачи, степень черноты, скорость движения среды, теплофизические характеристики движущейся среды), массопереноса (коэффициенты диффузии, кинетические константы, коэффициенты массоотдачи и массопередачи, скорость движения среды), гидродинамики (скорость и направление потоков, вязкость), входные потоки (гранулометрический состав, температура среды, давление, концентрация примесей).
Для всех этих параметров в справочниках приведены их средние значения, а на практике они имеют случайных характер, который определяется взаимным влиянием этих величин друг на друга, флуктуацией структуры потоков, особенностью конструкций аппаратов, машин и т.д.
Неопределенность может вызываться также погрешностями датчиков, исполнительных механизмов, информационных каналов, неточностью задания переменных в математической модели объекта, начальных и граничных условиях и т.п.
Неточность задания тех или иных параметров при расчетах с использованием детерминированной математической модели практически не принимается во внимание. Такой подход часто оказывается несостоятельным для решения современных задач управления технологическими процессами и производствами.
На рис. 5.6 представлена классификация неопределенностей. Основные типы неопределенностей приведены на рис. 5.6, а.
а)
ТИП НЕОПРЕДЕЛЕННОСТИ
Неизвест- 
 Неоднозначность
Неоднозначность 
 Недостоверность
Недостоверность
Физическая 
 Лингвистиче-
Лингвистиче-
Случайность 
 Неточность
Неточность
КЛАСС НЕОПРЕДЕЛЕННО-
|
|
|
Внутренняя |
|
|
|
|
|
|
|
Внешняя |
|
|
|
|
|||||||||
|
. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Техническиехарак- |
|
|
|
|
Техноло- |
|
|
|
|
|
Цель |
|
|
Среда |
|||||||||
б) |
|
теристики |
|
|
гическиехарактери |
|
|
|
|
|
|
|
|
|
|
Среда |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ло |
|
|
|
Гло |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Тех |
|
Робототех- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
нический |
|
|
Тепло- |
|
|
|
|
|
|
|
|
|
|
|
Пере- |
|||||
|
|
нологиче- |
|
комплекс |
|
|
массо- |
|
|
Гидро- |
|
|
Кине- |
|
менные |
|||||||||
|
|
ское обору- |
|
|
|
|
|
|
перенос |
|
|
динами- |
|
|
|
тика |
|
состоя- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
ка |
|
|
|
|
|
|
|
ния |
||||
|
|
о а е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.6. Классификация неопределенностей Неизвестность – этот тип неопределенности имеет место в том слу-
чае, когда неизвестна информация на выходе объекта исследования, т.е. нет технических средств и способов ее измерения.
Неоднозначность – имеет место в том случае, когда при строго определенной информации на входе некоторого технологического объекта, информация на выходе имеет различие. Неоднозначность может быть различной природы:
–физическая природа обуславливается случайностью или неточностью информации, что, как правило, определяется техническими измерительными средствами;
–лингвистическая природа имеет место в том случае, когда информация, используемая для анализа технологического объекта, может быть сформулирована на качественном (лингвистическом) уровне.
Недостоверность – этот тип неопределенности может быть в случае, когда информация об исследуемом объекте, явлении или технологических параметрах не является строго определенной (детерминированной).
На рис. 5.6, б представлены классы неопределенностей. Внутренняя неопределенность обуславливается техническими и технологическими характеристиками процессов и производств, а внешняя – определяется целью
исостоянием окружающей среды.
Начиная с конца XX в. развитие промышленных производств характеризуется внедрением прогрессивных технологий, обеспечивающих высо-
кий уровень энерго- и ресурсосбережения, ужесточением требований к качеству выпускаемой продукции и экологической чистоты. Это приводит к тому, что ошибки в управлении при использовании детерминированных математических моделей могут приводить к огромным экономическим потерям и способствуют возникновению аварийных ситуаций.
Для решения задач моделирования, управления и оптимизации в условиях неопределенности используют три подхода: стохастический, интервальный анализ и теорию нечетких множеств.
Построение стохастических моделей для решения задач оптимизации, проверки адекватности этих моделей требует проведения большого числа независимых экспериментальных исследований. Последнее сопряжено со значительными трудностями, которые обуславливаются как сложным аппаратурным оформлением современных ТП, так и ненаблюдаемостью некоторых из них, а также требует больших материальных затрат. Однако даже в том случае, когда применение теории управления стохастическими объектами строго обосновано и получены необходимые статистические характеристики, можно выделить основной недостаток, присущий большинству задач управления. В этих задачах функционал и ограничения рассматриваются в среднем, при этом не формализуются и не определяются выполнения технологических и технических требований на тех или иных режимах с заданной вероятностью.
Такой подход имеет ограниченное применение, так как совершенно не исключает возможности аварийных ситуаций, потерь качества продукта, нарушений технологических требований и условий. Причина этого, очевидно, заключается в том, что стремление приблизить работу реальных объектов к оптимальным режимам одновременно сопровождается приближением к предельным значениям технологических требований. В этих условиях учет стохастических свойств объектов лишь «в среднем» является технологически недопустимым. Тем более, невозможно использовать стохастические методы для вновь проектируемых производств, так как в этом случае в принципе нельзя провести прямые эксперименты.
Обычно на практике бывает известен лишь приближенно вид распределения, которому принадлежит неизвестная истинная плотность распределения, или неопределенный параметр задается только верхней и нижней границей, и о его поведении на границах и внутри интервала ничего не известно. В этом случае могут быть применены методы интервального анализа, когда неточность формализуется на основе использования интервальных оценок вместо фиксированных чисел.
Однако интервальный анализ имеет недостатки, которые зачастую могут привести к ошибкам в управлении, потери оптимального решения или к нарушению качественных показателей. Это объясняется, прежде всего, сложностью выбора интервальной оценки технологического параметра, так как при выборе малого интервала увеличивается вероятность нарушения качественных показателей, а при выборе большого интервала – возможно нахождение технологического режима далекого от оптимального.
Наиболее существенным недостатком интервальной оценки является не использование накопленного опыта эксплуатации ТП, имеющихся знаний операторов, технологов, специалистов по управлению.
Между тем, практика внедрения АСУТП показывает, что оператортехнолог зачастую решает задачи управления более успешно, чем эксплуатируемые системы управления. Это определяет необходимость использования качественной информации, получаемой от инженерно-технического персонала (экспертов), длительное время занимающегося эксплуатацией технологических процессов.
Проблема математической обработки качественной информации включает сбор, оценку достоверности, систематизацию, формализацию, переработку информации качественного характера с применением современных средств вычислительной техники.
Введенное Л. Заде понятие нечеткого множества как математического объекта, позволяющего формализовать термины словесного описания особенностей ТП, стимулировало развитие качественного этапа системного анализа и позволило подойти к решению указанной проблемы. При этом стали очевидны следующие достоинства подхода, основанного на аппарате теории нечетких множеств:

–«сжатие» качественной информации, причем степень сжатия определяется требуемой детализацией, которая определяется целью исследования и осуществляется с использованием методов инженерии знаний;
–наглядность и простота агрегирования и классификации сведений об исследуемом ТП, получаемых из различных источников;
–возможность применения качественной информации при переходе от смысловой к математической постановке задач;
–формирование стратегий управления ТП на основе качественной формализации действий оператора-технолога;
–синтез формальных вычислительных процедур для решения задач оптимизации и управления при нечеткой исходной информации и в нечетко определенных ситуациях задач оптимизации и управления с использование качественной информации.
5.4.Базовые понятия теории нечетких множеств
Пусть Х = {x} – универсальное множество, а С – определенное свойство. Обычное (четкое) непустое подмножество A универсального множества Х однозначно определяется характеристическим функционалом
QA(x) = |
|
(5.1) |
|
|
|
т.е. подмножество А определяется как совокупность объектов, имеющих некоторое общее свойство С, наличие или отсутствие которого у любого элемента х задается характеристическим функционалом, принимающим значение 1, когда x удовлетворяет свойству С, и 0 – в противном случае.
Пример 5.4. Рассмотрим множество X всех вещественных чисел между 0 и 10, которые назовем предметной областью. Определим подмножество A из X всех вещественных чисел в диапазоне между 4 и 7, т.е. A = [4, 7]
Покажем подмножество А в виде характерной функции, т.е. эта функция присваивает значение 1 или 0 каждому элементу в X, в зависимости от того, принадлежит ли элемент подмножеству или нет (рис. 5.7).
QA
1 
x
0 |
|
3 |
|
5 |
6 |
7 |
8 |
9 |
10 |
1 |
2 |
4 |
Рис. 5.7. Характеристическая функция
Определим элементы, которым присвоено значение 1, как элементы, принадлежащие множеству A, и элементы, которым присвоили значение 0, как элементы, не принадлежащие множеству A.
Сказанное можно записать следующей математической конструкцией: Х = {х [0, 10]} и А = {х [4, 7]} – подмножества Х: А Х. Это отношение включения можно выразить с помощью функции принадлежности множества:
А = {1|0, 2|0, 3|0, 4|1, 5|1, 6|1,7|1,8|0, 9|0, 10|0}.
Однако такие понятия, как множество «больших», «не очень больших» или «малых величин», уже не являются множествами в классическом смысле, так как не определены границы их степеней малости, которые позволили бы провести классификационную процедуру (5.1) и четко отнести каждый объект к определенному классу. Большинство классов реальных систем и технологических процессов относятся именно к такому нечетко определенному типу. Поэтому возникает необходимость введения понятия

о нечетком множестве как о классе с непрерывной градацией степеней принадлежности.
Понятие нечеткого множества – эта попытка математической формализации нечеткой информации для построения математических моделей. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, имеющие общее свойство, могут обладать этим свойством в различной степени и, следовательно, принадлежать к данному множеству с различной степенью.
Для нечеткого подмножества, являющегося расширением понятия множества в классическом смысле, на пространстве объектов Х = {x} вводится уже не функционал вида (5.1), а характеристическая функция, задающая для всех элементов степень наличия у них некоторого свойства, по которому они относятся к подмножеству А. Эта характеристическая функция для нечеткого множества традиционно носит название функции при-
надлежности.
Численное значение функции принадлежности характеризует степень принадлежности элемента некоторому нечеткому множеству, являющемуся в выражении естественного языка некоторой элементарной характеристикой явления (степени эффективности технологического режима, степени загрязнения среды, степени достоверности параметров модели и др.).
Нечеткое подмножество А множества Х характеризуется функцией принадлежности 
 : Х → [1, 0], которая ставит в соответствие каждому
: Х → [1, 0], которая ставит в соответствие каждому
элементу х Х число 
 (x) из интервала [0, 1], характеризующее степень
(x) из интервала [0, 1], характеризующее степень
принадлежности элемента х подмножеству А. Причем 0 и 1 представляют собой соответственно низшую и высшую степень принадлежности элемента к определенному подмножеству. Будем обозначать такое нечеткое мно-
жество 
 .
.
Пример 5.5. Пусть X = {1, 2, 3, …, 9, 10}. Тогда нечеткое множество 
 «большие числа» может быть представлено следующим образом:
«большие числа» может быть представлено следующим образом:
= {6|0,2, 7|0,5, 8|0,8, 9|1, 10|1}.
Это следует понимать следующим образом: числа 9 и 10 с абсолютной уверенностью можно отнести к «большим числам», 8 – есть «большое число» со степенью 0,8 и т.д., а числа 1, 2, …, 5 абсолютно не являются «большими числами». Можно использовать кусочно-линейную аппроксимацию функции принадлежности нечеткого множества, как показано на рис. 5.8.
µ(x) |
|
|
|
|
|
1 |
|
|
|
|
|
0,8 |
|
|
|
|
|
0,5 |
|
|
|
|
|
0,2 |
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
5 |
6 |
7 |
8 |
9 |
10 |
Рис. 5.8. Функция принадлежности нечеткого множества «большие числа»
Таким образом, значение функции принадлежности |
|
(х) элемента х |
к нечеткому множеству 
 можно интерпретировать как определенную экспертом (группой экспертов) степень соответствия элемента х понятию,
можно интерпретировать как определенную экспертом (группой экспертов) степень соответствия элемента х понятию,
формализованному нечетким множеством 
 .
.
5.4.1. Основные свойства нечетких множеств

Высотой нечеткого множества |
|
|
называется величина |
|
|
(х). |
|||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нечеткое множество |
|
|
нормально, если максимальное значение его функ- |
||||||||||
|
|
||||||||||||
ции принадлежности |
|
|
|
|
(х) = 1. При |
|
|
(х) < 1 нечеткое множест- |
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
во называется субнормальным.
Непустое субнормальное нечеткое множество можно преобразовать (нормализовать) в нормальное по формуле
(х) = .
Носителем нечеткого множества 
 называется четкое подмножество универсального множества Х, элементы которого имеют ненулевые значе-
называется четкое подмножество универсального множества Х, элементы которого имеют ненулевые значе-
ния функции принадлежности, т.е. sup (
 ) = {x: (х) > 0}, x X. Не-
) = {x: (х) > 0}, x X. Не-
четкое множество называется пустым, если его носитель является пустым множеством.
Ядром нечеткого множества 
 называется четкое подмножество множества Х, элементы которого имеют значения функции принадлежно-
называется четкое подмножество множества Х, элементы которого имеют значения функции принадлежно-
сти равные 1, т.е. core ( |
|
) = {x: |
|
(х) = 1}, x X. Ядро субнормального |
||
нечеткого множества пустое. |
|
|
|
|
||
|
|
|
|
|||
Множеством α-уровня (α-сечение) нечеткого множества |
|
называет- |
||||
ся четкое подмножество множества Х, элементы которого имеют значения
функции принадлежности большие или равные α, т.е. Аα = {x: |
|
(х) ≥ α}, |
α [0, 1]. |
|
|
Пример 5.6. Пусть 
 = {1|1; 2|0,8; 3|0,5; 4|0,1; 5|0}. Тогда А0,1 = {1, 2, 3, 4}, А0,5 = {1, 2, 3}.
= {1|1; 2|0,8; 3|0,5; 4|0,1; 5|0}. Тогда А0,1 = {1, 2, 3, 4}, А0,5 = {1, 2, 3}.
Иллюстрация определения носителя, ядра, α-сечение, α-уровня нечеткого множества приведена на рис. 5.9.
µ(х) 1
α |
α-уровень |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
0 |
|
|
|
ядро |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α-сечение |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
носитель |
||||
Рис. 5.9. Ядро, α-сечение, носитель нечеткого множества
5.4.2.Операции над нечеткими множествами
Снечеткими множествами можно производить все алгебраические действия, выполняемые для обычных множеств: получать их сумму (объединение), произведение (пересечение) и дополнение. При этом действия с нечеткими множествами сводятся к алгебраическим операциям с функциями принадлежности.
Объединение нечетких множеств. Пусть даны множества 
 и
и 
 . Их объединением
. Их объединением 


 называется нечеткое множество, функция принадлежности которого вычисляется следующим образом:
называется нечеткое множество, функция принадлежности которого вычисляется следующим образом:

|
(х) = |
|
( |
|
(x), |
|
(x)). |
|
|
|
|
|
|
|
|
Объединение соответствует союзу или и его можно записывается как
|
(х) = |
|
(x) |
|
(x), |
где символ 
 соответствует операции взятия max.
соответствует операции взятия max.
Пример 5.7. Пусть нечеткие множества |
|
и |
|
|
заданы в табличной |
||||||||||||||||||||||||
форме: |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x1 |
x2 |
|
x3 |
|
x4 |
|
|
|
|
|
x1 |
x2 |
|
x3 |
|
x4 |
|
||||||||
|
|
0,1 |
0,2 |
|
0,3 |
|
1 |
|
|
|
|
0,5 |
|
0,9 |
|
0,1 |
|
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
x3 |
|
x4 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0,5 |
|
0,9 |
0,3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5.8. Пусть 
 – нечеткий интервал между 5 и 8 и
– нечеткий интервал между 5 и 8 и 
 – нечеткое число, приблизительно 4. Объединение нечеткого множества между 5 и 8 с приблизительно 4 показывается на рис. 5.10 (жирная линия).
– нечеткое число, приблизительно 4. Объединение нечеткого множества между 5 и 8 с приблизительно 4 показывается на рис. 5.10 (жирная линия).
Пересечение нечетких множеств. Пусть даны множества 
 и
и 
 . Их пересечением
. Их пересечением 


 называется нечеткое множество, функция принадлежности которого вычисляется следующим образом:
называется нечеткое множество, функция принадлежности которого вычисляется следующим образом:
|
(х) = |
|
( |
|
(x), |
|
(x)). |
|
|
|
|
|
|
|
|
Пересечение соответствует союзу и и его можно записать как
|
(х) = |
|
(x) |
|
(x), |
где символ 
 соответствует операции взятия min.
соответствует операции взятия min.
Пример 5.9. Пусть нечеткие множества |
|
и |
|
|
заданы в табличной |
||||||||||||||||||||||||||||
форме: |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x1 |
|
x2 |
|
x3 |
|
x4 |
|
|
|
|
|
|
|
x1 |
|
x2 |
|
x3 |
|
x4 |
|
||||||||
|
|
0,1 |
|
0,4 |
|
0,5 |
|
1 |
|
|
|
|
|
|
0,7 |
|
0,9 |
|
0,3 |
|
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
x3 |
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
0,1 |
|
0,4 |
0,3 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
5 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|||
Рис. 5.10. Функция принадлежности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
||
0 |
4 |
5 |
|
8 |
|
|
|
|
Рис. 5.11. Функция принадлежности |
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Пример 5.10. Пусть |
|
– нечеткий интервал между 5 и 8 и |
|
– не- |
||||
|
|
|||||||
четкое число, приблизительно 4. Пересечение нечеткого множества между 5 и 8 с приблизительно 4 показывается на рис. 5.11 (жирная линия).
|
Дополнение нечеткого множества. Дополнением нечеткого множест- |
|||||||||
ва |
служит также нечеткое множество , функция принадлежности ко- |
|||||||||
торого вычисляется следующим образом: |
|
|||||||||
|
(х) = 1 – |
|
|
(x). |
|
|
задано в табличной |
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
5.11. Пусть нечеткое множество |
||||||||
форме: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
|
x3 |
x4 |
|
|
|
|
|
0,2 |
|
0 |
|
|
0,3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x1 |
|
x2 |
|
x3 |
x4 |
|
|
|
|
|
0,8 |
|
1 |
|
|
0,7 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Дополнение нечеткого множества 
 можно показать графически
можно показать графически
(рис. 5.12).
В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в так называемых треугольных нормах и конормах. Приведенные выше реализации операций пересечения и объединения – наиболее распространенные случаи t-нормы и t-конормы.
(х)
1
х
Рис. 5.12. Функция принадлежности |
|
(х) |
Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и гауссова формы функции принадлежности.
Треугольная функция принадлежности (рис. 5.13) определяется тройкой чисел (a, b, c), и ее значение в точке x вычисляется согласно выражению:

При b – a = c – b имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a, b, c).
µ(x)
1
x
0 |
a |
b |
c |
|
|
|
|
Рис. 5.13. Треугольная функция принадлежности
µ(x)
1
x
a |
b |
c |
d |
|
|
|
|
Рис. 5.14. Трапецеидальная функция принадлежности
Аналогично для задания трапецеидальной функции принадлежности (рис. 5.14) необходима четверка чисел (a, b, c, d):
|
|
|
x −a |
, |
a ≤ x ≤ b; |
|
|
|
|
||
|
|
b −a |
|||
|
1, |
|
b ≤ x ≤ c; |
||
µ(x) = |
|
d − x |
|
|
|
|
|
|
c ≤ x ≤ d ; |
||
|
|
d −с , |
|||
|
в остальных случаях. |
||||
0 |
|||||
При b – a = d – c трапецеидальная функция принадлежности принимает симметричный вид.
Функция принадлежности гауссова типа (рис. 5.15) описывается формулой
.
и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр σ отвечает за крутизну функции.
