ЗМІСТОВИЙ МОДУЛЬ. ЕКОНОМЕТРИЧНІ МОДЕЛІ
Тема 9 принципи побудови економетричних моделей.
ПАРНА ЛІНІЙНА РЕГРЕСІЯ
Лабораторна робота №16-17. Парна лінійна регресія
Приклади розв’язування задач
Задача 9.1. (знаходження оцінок параметрів моделі)
Знайти оцінки параметрів моделі 
методом
найменших квадратів, якщо задані вектори
Х та У. Обчислить дисперсію залишків
цієї моделі, середнє квадратичне
відхилення, коефіцієнт кореляції,
коефіцієнт еластичності.
У |
10 |
11 |
12 |
15 |
16 |
18 |
20 |
21 |
23 |
23 |
Х |
3 |
4 |
4 |
5 |
6 |
7 |
9 |
9 |
10 |
11 |
Рішення
Нехай залежність між Х та У описується
прямою лінією , де u - залишки (збурення
моделі). Розрахункові значення (Ур)
обчислимо, користуючись такою моделлю:
(9.1)
Для обчислень можна використовувати таку допоміжну таблицю. Для перевірки таблиця вже має заповнені стовпці.
Таблиця 9.1
№ |
У |
Х |
Х2 |
ХУ |
Х-Хср |
У-Уср |
(Х-Хср)2 |
(Х-Хср) * ( У-Уср) |
(У-Уср)2 |
Ур |
U= У-Ур |
U2 |
1 |
10 |
3 |
9 |
30 |
-3,80 |
-6,90 |
14,44 |
26,22 |
47,61 |
10,44 |
-0,44 |
0,19 |
2 |
11 |
4 |
16 |
44 |
-2,80 |
-5,90 |
7,84 |
16,52 |
34,81 |
12,14 |
-1,14 |
1,29 |
3 |
12 |
4 |
16 |
48 |
-2,80 |
-4,90 |
7,84 |
13,72 |
24,01 |
12,14 |
-0,14 |
0,02 |
4 |
15 |
5 |
25 |
75 |
-1,80 |
-1,90 |
3,24 |
3,42 |
3,61 |
13,84 |
1,16 |
1,35 |
5 |
16 |
6 |
36 |
96 |
-0,80 |
-0,90 |
0,64 |
0,72 |
0,81 |
15,54 |
0,46 |
0,21 |
6 |
18 |
7 |
49 |
126 |
0,20 |
1,10 |
0,04 |
0,22 |
1,21 |
17,24 |
0,76 |
0,58 |
7 |
20 |
9 |
81 |
180 |
2,20 |
3,10 |
4,84 |
6,82 |
9,61 |
20,64 |
-0,64 |
0,41 |
8 |
21 |
9 |
81 |
189 |
2,20 |
4,10 |
4,84 |
9,02 |
16,81 |
20,64 |
0,36 |
0,13 |
9 |
23 |
10 |
100 |
230 |
3,20 |
6,10 |
10,24 |
19,52 |
37,21 |
22,34 |
0,66 |
0,43 |
10 |
23 |
11 |
121 |
253 |
4,20 |
6,10 |
17,64 |
25,62 |
37,21 |
24,04 |
-1,04 |
1,09 |
Σ |
169 |
68 |
534 |
1271 |
0,00 |
0,00 |
71,60 |
121,80 |
212,90 |
169,00 |
0,00 |
5,70 |
Обчислимо значення оцінок параметрів моделі за допомогою відхилень середніх арифметичних , за формулою:
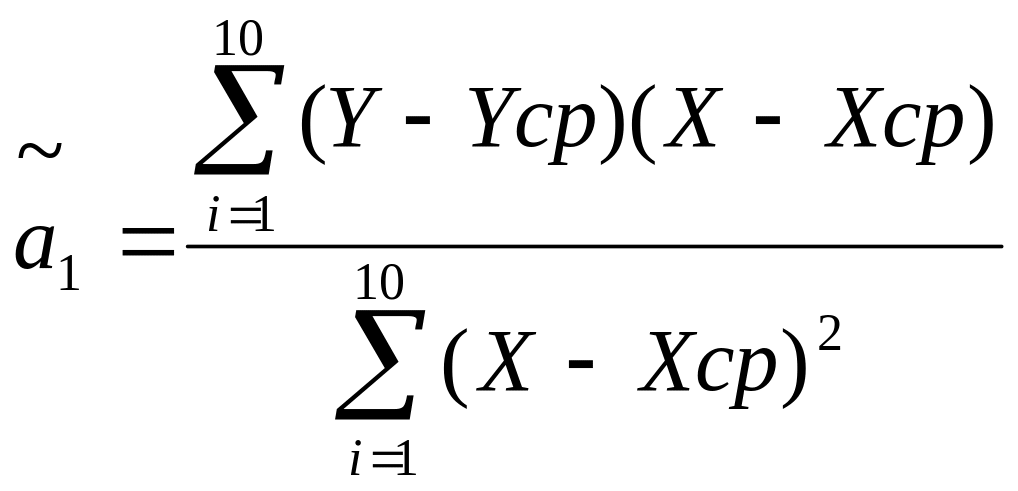=1,7
та
Що дорівнює відповідно 5,33.
Обчислимо значення Ур (розрахункове) використовую формулу .
Обчислимо залишки за формулою = У-Ур та їх квадрати, та відповідні суми стовпців.
Обчислимо не зсунену оцінку дисперсії
залишків
.
Вона дорівнює 0,71 та середнє квадратичне
відхилення . використовуючи формулу
Коефіцієнт кореляції обчислимо за формулою (9.2):
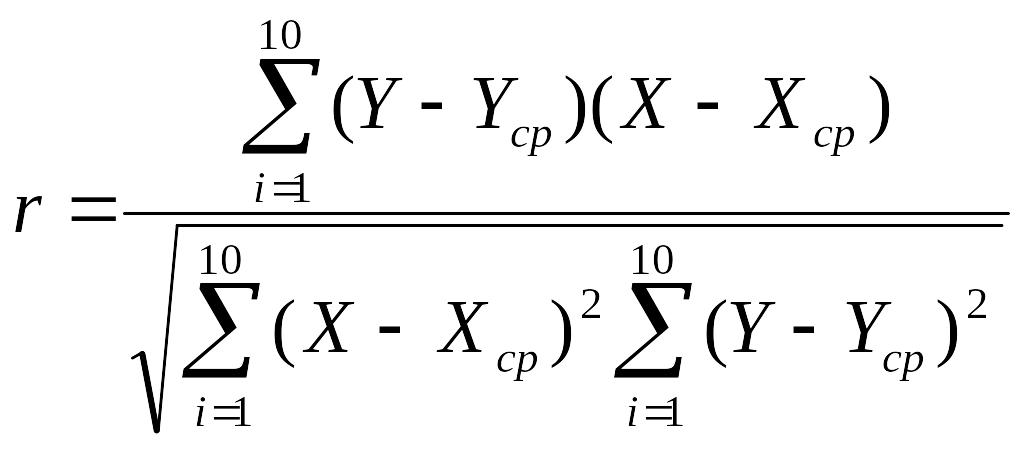
=0,986 (9.2)
Коефіцієнт еластичності для парної регресії обчислимо за формулою:
=0,68 (9.3)
Задача 9.2. (перевірка якості, точності та надійності моделі)
На основі моделі попередньої задачі виконати наступне:
- перевірити гіпотезу про значущість коефіцієнта кореляції, оцінок параметрів моделі (за допомогою t – тест Стюдента);
- знайти інтервал довіри для параметра кутового коефіцієнта регресії, надійні межі для вільного члена;
- перевірити модель на адекватність статистичним даним (F – тест, значущість 95%)
- знайти точковий прогноз та інтервал довіри окремого значення Упр та для математичного сподівання значення Упр якщо Хпр=15.