Задачи.

1. Найти коэффициент корреляции между величинами X и y, совместный закон распределения которых задан следующей таблицей:

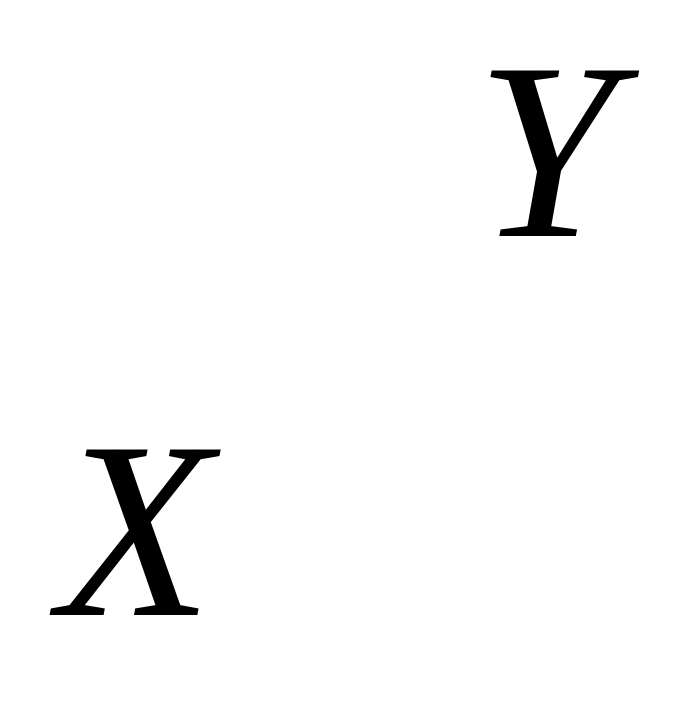
	1	2	3	4
10	0,2	0,02	0,01	0	0,23
20	0,03	0,3	0,02	0	0,35
30	0,02	0,1	0,2	0,1	0,42
	0,25	0,42	0,23	0,1	1

2. Двумерная случайная величина распределена по закону, приведенному в таблице:

Y X	0	1
-1	0,1	0,2
0	0,2	0,3
1	0	0,2

Определить коэффициент корреляции величин X и Y.

3. Двумерная случайная величина равномерно распределена в области D, ограниченной прямыми X=0, Y=0 и X+Y=4. Определить коэффициент корреляции величин X и Y.

4. Число Х выбирается случайным образом из множества (1,2,3). Затем из того же множества выбирается наудачу число Y, равное или большее Х. Найти коэффициент корреляции.

Глава 6. Цепи Маркова

6.1 Цепи Маркова с дискретным временем

Краткие теоретические сведения.

1. Цепи Маркова представляют собой частный вид случайных процессов. Случайный процесс называется марковским, если для любого момента времени вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, когда и каким образом система пришла в это состояние.

Цепью Маркова с дискретным временем называют цепь, изменение состояний которой происходит в определенные фиксированные моменты времени.

Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени.

Переходной вероятностью называют условную вероятность того, что из состояния в итоге следующего испытания система перейдет в состояние .

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

,

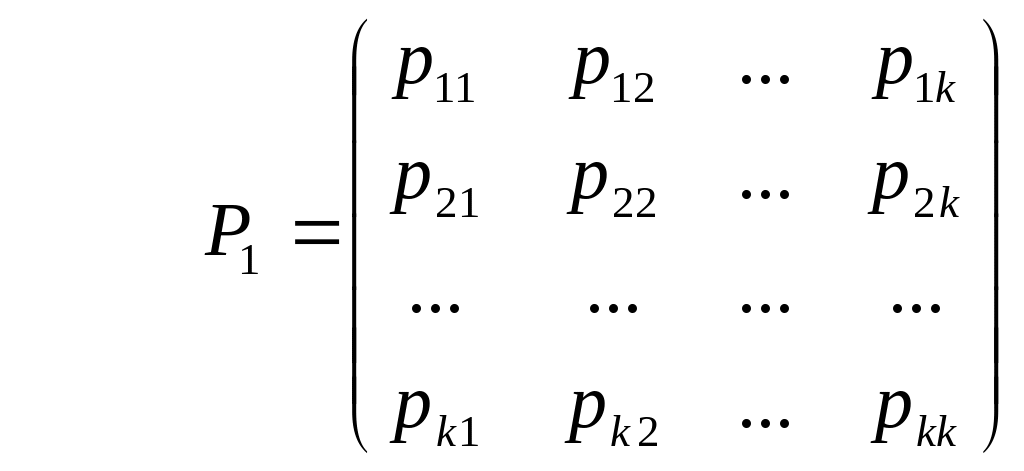где - вероятности перехода за один шаг.

Основные свойства матрицы перехода:

1. Элементы каждой строки матрицы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и вероятность отсутствия перехода.

2. Элементы столбцов задают вероятности всех переходов системы за один шаг в заданное состояние.

3. В каждой строке матрицы вероятности перехода из состояния в любое возможное состояние образуют полную группу, поэтому 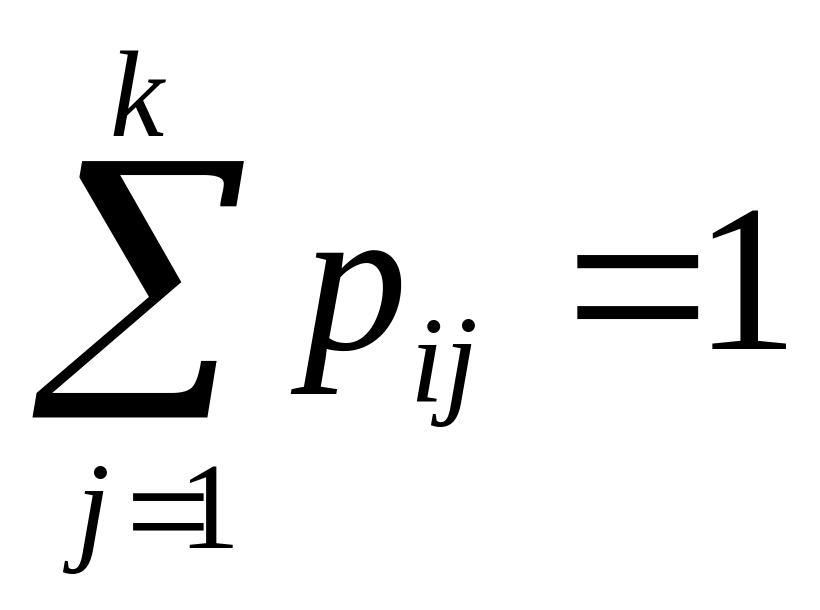(сумма вероятностей строки = 1)

4. По главной диагонали матрицы перехода стоят вероятности 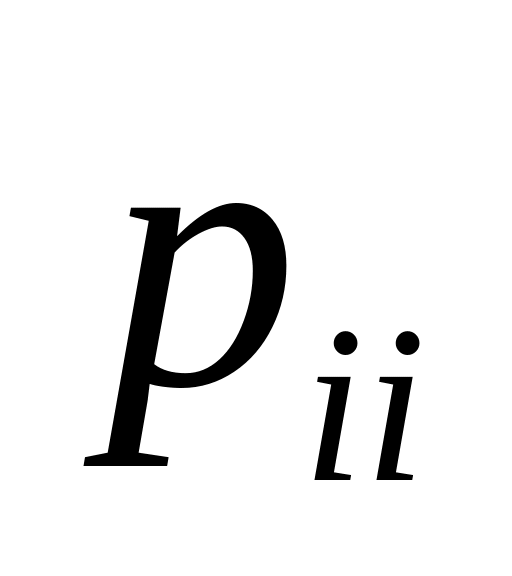того, что система не выйдет из состояния, а останется в нем.

2. Часто требуется при известных переходных вероятностях , найти вероятность перехода из состояния в состояние за шагов.

Равенство Маркова через промежуточные шаги).

Как следствие из нее

3. Начальным распределением Марковской цепи называется распределение вероятностей состояний в начале процесса , где - вероятность нахождения системы в начальный момент времени в состоянии . В частности, если начальное состояние системы в точности известно, то начальная вероятность , а все остальные равны нулю.

Если для однородной цепи Маркова заданы начальное распределение вероятностей и матрица перехода, то вероятности состояний системы на -ом шаге вычисляется

или

,

где ( ) задает вероятности пребывания системы в состояниях после шагов, а задает начальное распределение вероятностей состояний системы, - матрица перехода.

4. Предельные вероятности состояний дискретной Марковской цепи определяются с помощью решения системы уравнений:

,

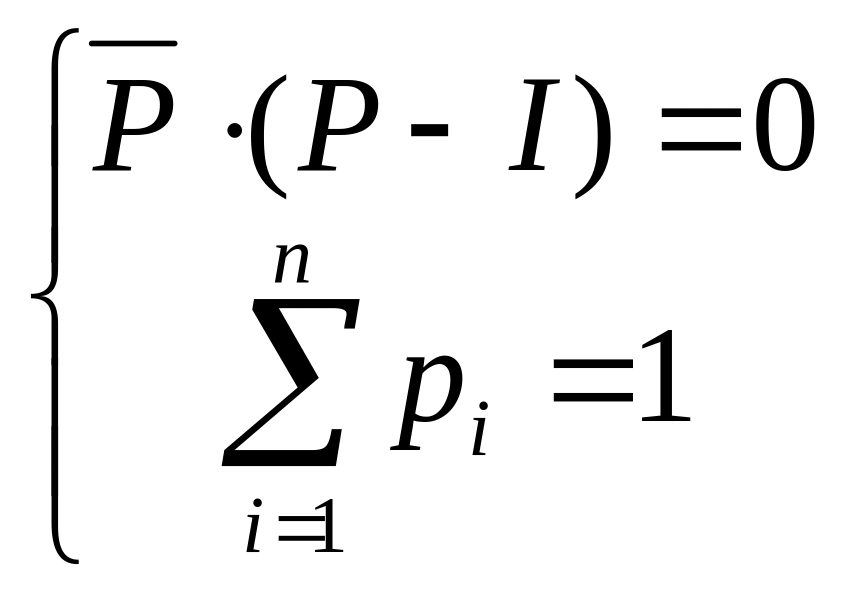где - вектор-строка, компонентами которого являются предельные вероятности состояний , - матрица перехода, - единичная матрица, а второе соотношение учитывает условие нормировки.