
- •Академия управления
- •Содержание
- •Часть I. Задачи по теории вероятностей 4
- •Глава 1. События и вероятности 4
- •Часть I. Задачи по теории вероятностей Глава 1. События и вероятности
- •1.1 Элементы комбинаторики
- •1.2 Пространство элементарных событий. Полная группа событий. Операции над событиями
- •Задачи.
- •1.3 Задачи на классическое определение вероятности и гипергеометрическое распределение
- •Гипергеометрическое распределение (урновая схема)
- •Задачи.
- •1.4 Геометрические вероятности
- •Задачи.
- •1.5 Формулы сложения и умножения вероятностей
- •Понятия:
- •Формулы умножения вероятностей.
- •Формулы сложения вероятностей.
- •Задачи.
- •1.6 Формула полной вероятности и формула Байеса
- •1. Формула полной вероятности
- •2. Формула Байеса
- •Задачи.
- •1.7 Схема Бернулли. Предельные теоремы для схемы Бернулли
- •5. Локальная теорема Муавра-Лапласа.
- •Задачи.
- •Глава 2. Случайные величины и законы их распределения
- •2.1 Законы и функции распределения случайных величин. Математическое ожидание и дисперсия
- •Задачи.
- •2.2 Важнейшие распределения: биномиальное, Пуассона, показательное, равномерное и геометрическое
- •Задачи.
- •2.3 Нормальное распределение и его свойства
- •Задачи.
- •2.4 Двумерные случайные величины. Совместная функция и плотность распределения случайных величин
- •5. Вероятность попадания в прямоугольную область:
- •Задачи.
- •Часть II. Математическая статистика Глава 3. Доверительные интервалы
- •3.1 Доверительные интервалы при известной и неизвестной дисперсии
- •Задачи.
- •Глава 4. Проверка статистических гипотез
- •4.1 Сравнение дисперсий
- •4.1.1 . Сравнение двух дисперсий нормальных генеральных совокупностей
- •Задачи.
- •4.1.2. Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности
- •Задачи.
- •4.2 Сравнение средних генеральных совокупностей
- •4.2.1. Сравнение двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки)
- •Задачи.
- •4.2.2. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки.
- •Задачи.
- •4.2.3. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности
- •Задачи.
- •Задачи.
- •Глава 5. Элементы теории корреляции
- •Задачи.
- •1. Найти коэффициент корреляции между величинами X и y, совместный закон распределения которых задан следующей таблицей:
- •Глава 6. Цепи Маркова
- •6.1 Цепи Маркова с дискретным временем
- •Задачи.
- •6.2 Цепи Маркова с непрерывным временем
- •Уравнение Колмогорова
- •Финальные вероятности состояний системы.
- •Задачи.
- •6.3. Задачи на использование схемы гибели и размножения
- •Задачи.
- •Глава 1.
- •1.1 Элементы комбинаторики.
- •1.3 Классическое определение вероятности и урновая схема.
- •1.4 Геометрические вероятности.
- •1.5 Формулы сложения и умножения вероятностей.
- •1.6 Формула полной вероятности и формула Байеса.
- •1.7 Схема Бернулли. Предельные теоремы для схемы Бернулли.
- •Глава 2.
- •2.1 Законы и функции распределения случайных величин.
- •2.2 Важнейшие распределения.
- •2.3 Нормальное распределение и его свойства.
- •2.4 Двумерные случайные величины.
- •Глава 3.
- •3.1 Доверительные интервалы при известной и неизвестной дисперсии
- •Глава 4.
- •4.1 Сравнение дисперсий.
- •4.2 Сравнение средних генеральных совокупностей.
- •Глава 5. Элементы теории корреляции.
- •Глава 6.
- •6.1 Дискретные цепи Маркова.
- •Непрерывные цепи Маркова.
- •Задачи на использование схемы гибели и размножения.
- •Приложения
2.3 Нормальное распределение и его свойства
Краткие теоретические сведения.
1. Непрерывная
случайная величина Х имеет нормальный
закон распределения с параметрами
и
![]() ,если
ее плотность вероятности имеет вид:
,если
ее плотность вероятности имеет вид:
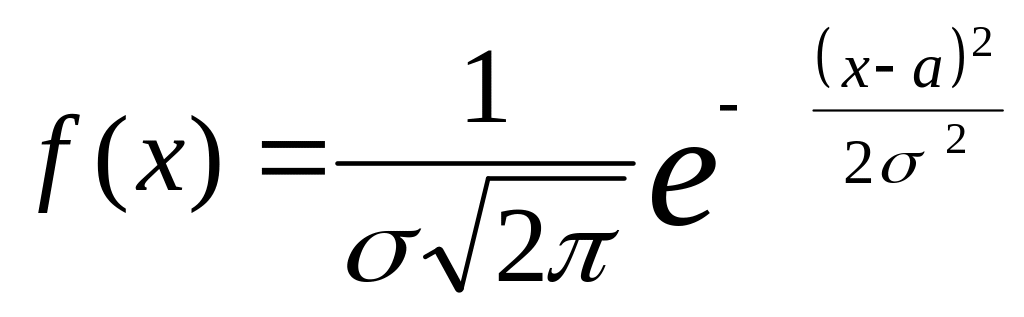
где
![]() и
- математическое ожидание и среднее
квадратическое отклонение.
и
- математическое ожидание и среднее
квадратическое отклонение.
2. Вероятность попадания нормально распределенной случайной величины в заданный интервал (, ) определяется формулой:
![]() ,
,
где Ф(х) –функция Лапласа
3. Вероятность того, что нормально распределенная случайная величина отклонится от своего математического ожидания по модулю не больше положительного числа , равна:
![]()
4. Если в качестве
взять утроенное
СКО, то справедливо соотношение
![]() известное, как правило “трех сигм”.
известное, как правило “трех сигм”.
Задачи.
1. Случайная величина Х представляет цену акции некоторого предприятия. Она распределена нормально с математическим ожиданием a = 88 д.е. и С.К.О. = 12 д.е. Определить вероятность того, что в случайно выбранный день года цена на акцию была: а) более 100 д.е.; б) менее 100 д.е.; в) от 70 до 90 д.е.
2. Фирма, занимающаяся продажей товаров по каталогу, ежемесячно получает по почте заказы. Число этих заказов распределено по нормальному закону со средним квадратическим отклонением = 440 и неизвестным математическим ожиданием. В 90% случаев число ежемесячных заказов превышает 10000. Найти ожидаемое среднее число заказов, получаемых фирмой за месяц.
3. Предприятие А покупает у предприятия В детали к контрольным приборам. Деталь, размер которой отличается от установленного более чем на 0,02 мм, считается дефектной. Предприятие А требует от предприятия В, чтобы доля брака не превышала 1% деталей. Если предприятие В выполняет требования предприятия А, то каким должно быть допустимое максимальное стандартное отклонение деталей? Размер деталей распределен по нормальному закону.
4. Эксперимент показал, что стандартное отклонение срока службы автопокрышек составляет 3000 км. Если необходимо, чтобы 80% выпускаемых автопокрышек имели срок службы не менее 35000 км, то какой наименьший средний срок службы автопокрышек должен быть заложен в расчетах технического отдела? Считать срок службы автопокрышек нормально распределенным.
5. Руководство предприятия анализирует эффективность обслуживания клиентов. Выяснилось, что среднее время выполнения заказа равно 5,2 часа, однако для 20% заказов потребовалось 12 и более часов. Учитывая, что время выполнения заказа есть нормально распределенная случайная величина, определить фактическое стандартное отклонение времени обслуживания клиентов.
6. Определить
закон распределения случайной величины
Х, если ее плотность вероятности имеет
вид:
![]()
Найти:
![]()
7. Известно,
что
![]() Найти
Найти
![]()
8. Рост взрослых
мужчин является случайной величиной,
распределенной по нормальному закону
![]() Определить: а) плотность вероятности;
б) функцию распределения; в) вероятность
того, что ни один из трех наудачу выбранных
мужчин не будет иметь рост менее 180 см.
Определить: а) плотность вероятности;
б) функцию распределения; в) вероятность
того, что ни один из трех наудачу выбранных
мужчин не будет иметь рост менее 180 см.
9. Установлено, что случайная величина
![]() Найти
Найти
![]()
10. Срок
безотказной работы телевизора представляет
собой случайную величину
![]() Найти вероятность того, что телевизор
проработает: а) не менее 15 лет; б) от 6 до
9 лет. в) от 9 до 15 лет.
Найти вероятность того, что телевизор
проработает: а) не менее 15 лет; б) от 6 до
9 лет. в) от 9 до 15 лет.
11. Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием 50 мм. Фактически длина изготовленных деталей не менее 49,4 мм и не более 50,6 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 50,2 мм; б) меньше 49,8 мм.
12. Станок-автомат
изготавливает цилиндрические детали,
контролируя их диаметры Х. Считая, что
случайная величина Х распределена
нормально с параметрами
![]() найти интервал, в котором с вероятностью
0,9973 будут заключены диаметры изготовленных
деталей.
найти интервал, в котором с вероятностью
0,9973 будут заключены диаметры изготовленных
деталей.
13. Среднее квадратическое отклонение случайной величины, распределенной по нормальном закону, равно 4 см, а математическое ожидание равно 25 см. Найти границы, в которых с вероятностью а) 0,95; б) 0,7 следует ожидать значение случайной величины.
14. Независимые случайные величины X и Y распределены нормально, причем
![]()
Записать плотность вероятности и функцию распределения их суммы.
15. Суммарная месячная выручка 10 малых предприятий в среднем 16000 д.е. В 75% случаев эта выручка отклоняется от средней не более чем на 1000 д.е. Найти вероятность того, что очередная месячная выручка находится в интервале между 10000 и 15000 д.е.
16. При измерении
детали получаются случайные ошибки,
подчиненные нормальному закону с
параметром
![]() .
Найти вероятность того, что измерение
произведено с ошибкой, не превосходящей
15мм.
.
Найти вероятность того, что измерение
произведено с ошибкой, не превосходящей
15мм.
17. Случайная величина Х распределена нормально со средним М(Х)=10, а вероятность ее попадания в интервал (5,15) равна 0,8. Найти вероятность попадания Х в интервал (9,10).
18. Случайная величина Х является нормально распределенной. Ее математическое ожидание равно 18, а вероятность ее попадания в интервал (16,20) равна 0,98. Найти среднее квадратичное отклонение случайной величины.
19. Случайная величина Х является нормально распределенной. Ее математическое ожидание равно 10, а среднее квадратическое отклонение равно 2. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (9, 12).
20. Определить
среднеквадратическую ошибку измерительного
прибора, если систематических ошибок
он не имеет, а случайные ошибки измерения
имеют нормальное распределение и с
вероятностью 0,9 не выходят за
![]() мм.
мм.
21. Текущая цена ценной бумаги представляет собой нормально распределенную случайную величину Х со средним 100 у.е. и дисперсией 9. Найти вероятность того, что цена актива будет находиться в пределах от 91 до 109 у.е.
22. Случайная
величина Х распределена по нормальному
закону, причем М(Х)=10. Найти
![]() ,
если известно
,
если известно
![]() .
.
23. Найти вероятность того, что нормальная случайная величина с математическим ожиданием, равным 3, и дисперсией, равной 4, примет значения: а) в интервале (-1;5); б) не более 8; в) не менее 5; г) в интервале (-3;9).
24. Взвешивание
большегрузных автомобилей производится
с ошибкой, подчиненной нормальному
закону с параметром
![]() Найти вероятность того, что взвешивание
будет произведено с ошибкой, не
превосходящей 30 кг.
Найти вероятность того, что взвешивание
будет произведено с ошибкой, не
превосходящей 30 кг.
25. Для силы тока в цепи используются специальные датчики.
Определить среднюю квадратическую ошибку датчика, если он не имеет систематических ошибок, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ±0,2 микроампера.
26. Сообщение передается последовательностью амплитудно-модулированных импульсов с заданным шагом квантования ∆ (∆ – наименьшая разность амплитуд импульсов). В процессе передачи на сообщение накладываются шумы, распределенные по нормальному закону N(0, σ). Если мгновенное значение шума превышает половину шага квантования, то при передаче сообщения возникает ошибка. Определить, при каком минимально допустимом шаге квантования ∆ вероятность ошибки из-за шумов не превысит 0,1.
27. СВ X–ошибка
измерительного прибора – распределена
нормально с дисперсией 16 мА![]() .
Систематическая ошибка прибора
отсутствует. Вычислить вероятность
того, что в пяти независимых измерениях
ошибка: а) превысит по модулю 6 мА не
более трех раз; б) хотя бы один раз
окажется в интервале (0,5; 3,5) мА
.
Систематическая ошибка прибора
отсутствует. Вычислить вероятность
того, что в пяти независимых измерениях
ошибка: а) превысит по модулю 6 мА не
более трех раз; б) хотя бы один раз
окажется в интервале (0,5; 3,5) мА
