Лабораторная работа № 5 исследование режимов работы трехфазных цепей
Цель работы: исследование режимов работы трехфазных цепей при соединении приемников звездой и треугольником.
1. Основные теоретические сведения
1.1. Основные определения
Трехфазной электрической цепью называется совокупность трех электрических цепей, в которых действуют источники энергии с электродвижущими силами одной и той же частоты, сдвинутыми друг относительно друга по фазе. Отдельная электрическая цепь, входящая в трехфазную цепь, называется фазой.
Совокупность ЭДС источников питания трехфазной цепи называется трехфазной системой ЭДС. Если ЭДС равны по величине и сдвинуты друг относительно друга на одинаковый угол, система ЭДС называется симметричной. Обычно трехфазные генераторы дают симметричную систему ЭДС.
Порядок, в котором ЭДС в фазах генератора проходят через одинаковые значения (например, через положительные максимумы), называется порядком чередования фаз. Если обозначить фазы генератора буквами А, В, С и принять за начало отсчета момент, когда ЭДС фазы А проходит через нуль, то при прямом порядке чередования фаз генератора ЭДС фазы В отстает, а ЭДС фазы С опережает ЭДС фазы А на 120° и мгновенные значения ЭДС равны
,
,
.
Векторная диаграмма системы ЭДС трехфазного генератора имеет вид как на рис.1
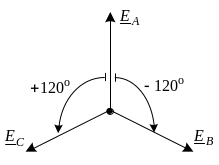
Рис.1
Для комплексов действующих значений фазных ЭДС имеем
,
,
.
Обозначая
,
=
,
Получим
,
,
.
Величина
называется фазным оператором (множителем).
Как видно из приведенных соотношений,
.
Основными способами соединения фаз генераторов и приемников в трехфазной цепи являются соединения звездой и треугольником.
Рис. 2 Рис. 3
При
соединении фаз генератора звездой
(рис.2) концы фаз
,
,
объединяют в одну точку, называемую
нейтральной или нулевой
точкой.
При соединении фаз генератора треугольником
(рис. З) конец одной фазы соединяют с
началом следующей.
Соединение сопротивлений нагрузки в звезду или треугольник подобно соединению фаз генератора на рис.2 и 3. Если при этом комплексы полных сопротивлений фаз нагрузки равны, то такая нагрузка называется симметричной, при неравенстве сопротивлений - несимметричной. Если сопротивления нагрузки имеют одинаковый характер (все три сопротивления только активные, только емкостные или только индуктивные), то такая нагрузка называется однородной, в противном случае имеем неоднородную нагрузку.
1.2. Трехфазная цепь при соединении генератора и нагрузки звездой.
1.2.1. Схема без нейтрального провода
На рис.4 представлена трехфазная цепь при соединении фаз генератора и нагрузки звездой. Провода, соединяющие начала фаз генератора и нагрузки, называются линейными. Рассматривается случай, когда сопротивлениями линейных проводов можно пренебречь.
Рис. 4
На схеме показаны условные положительные направления токов и напряжений. Напряжения между началом и концом фазы называются фазными. Напряжения между любыми двумя линейными проводами - линейными. Напряжение между нулевыми точками приемника и генератора – напряжением смещения нейтрали.
Токи в фазах называются фазными токами, токи в линейных проводах - линейными. Из схемы видно, что при соединении нагрузки звездой линейные токи равны фазным.
Для
определения токов
,
,
при заданных ЭДС генератора и сопротивлениях
фаз можно применить метод двух узлов.
В соответствии с этим методом имеем
,
,
,
.
Здесь
,
,
.
На рис.5 показана векторная диаграмма токов, совмещенная с топографической диаграммой напряжений для схемы, изображенной на рис.4.
Рис. 5
Началом
векторной диаграммы токов целесообразно
выбрать точку
.
Симметричная нагрузка. Пусть в цепи, схема которой показана на рис. 4
.
Как отмечалось, такая нагрузка называется симметричной.
Применяя метод двух узлов, получим
так
как
,
.
По сравнению с предыдущим случаем расчет токов упрощается
,
,
.
Как
видно, в случае симметричной нагрузки
ЭДС
напряжения
и токи в фазах образуют симметричные
системы векторов. Значит, расчет
трехфазной
цепи в этом случае можно вести для одной
фазы (обычно для фазы
).
Рассчитав ток и
напряжение
в фазе
,
напряжение и ток в фазе
получим, умножая соответствующие
величины фазы
на
,
a
в фазе
- на
.
Векторная диаграмма токов, совмещенная с топографической диаграммой напряжений, для симметричной нагрузки представлена на рис. 6.
Рис. 6 Рис. 7
При симметричной нагрузке отношение величины линейного и фазного напряжений на нагрузке постоянно и не зависят от ее величины и характера.
Действительно, из рис.7 видно, что
=
.
1.2.2. Схема с нейтральным (нулевым) проводом
Нейтральным
называется провод, соединяющий нулевые
точки генератора
и приемника
.
Рассматривается случай, когда
сопротивлением нейтрального провода
можно пренебречь. В этом случае точки
и
имеют одинаковый потенциал, т.е.
.
Токи рассчитываются по формулам:
,
,
,
,
где
– ток в нейтральном проводе
В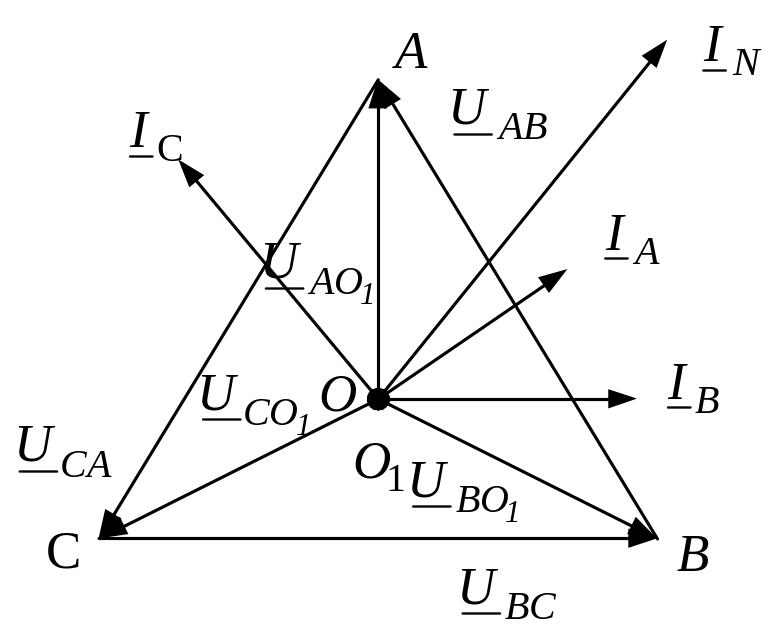
екторная
диаграмма токов, совмещенная с
топографической диаграммой напряжений,
для схемы с нулевым проводом приведена
на рис.8.
Рис. 8