2. Позиционные игры

Не давая пока никаких формальных определений, рассмотрим примеры игр другого типа, в которых ходы делаются по очереди, каждый ход и каждое новое (после этого хода) состояние игры немедленно становятся известными обоим игрокам.

Пример 7. Игра «ним». В этой игре на стол между двумя игроками выкладывается неко-торое количество фишек. При каждом ходе игрок должен разделить одну из имеющихся групп фишек на два непустых подмножества разных размеров. Например, 6 фишек можно разделить на группы 5 и 1 или 4 и 2, но не 3 и 3. В начале игры все фишки образуют одну группу. После 1-го деления появится две группы, после 2-го деления – 3 группы, и т.д. Игрок, который не смо-жет больше сделать ход, проигрывает. На рис.7 показан граф игры «ним» для 7 фишек. Каждая вершина этого графа соответствует одному из возможных разбиений 7 фишек на группы. Их можно назвать позициями в игре. Позиция 5-1-1 означает, что имеется три группы: в 1-ой группе – 5 фишек, а в двух других – по 1-ой фишке. Дуги соответствуют возможным ходам иг-рока в данной позиции. В позиции 5-1-1 есть две возможности: разделить группу из 5 фишек на группы из 3-ёх и 2-ух фишек или на группы из 4-ёх и 1-ой фишки. Это значит, что из пози-ции 5-1-1 можно перейти в позиции 3-2-1-1 и 4-1-1-1. Позиции 2-2-2-1, 2-2-1-1-1 и 2-1-1-1-1-1 называются финальными, поскольку из них никуда нельзя перейти. Позиция 7 назы-вается начальной.

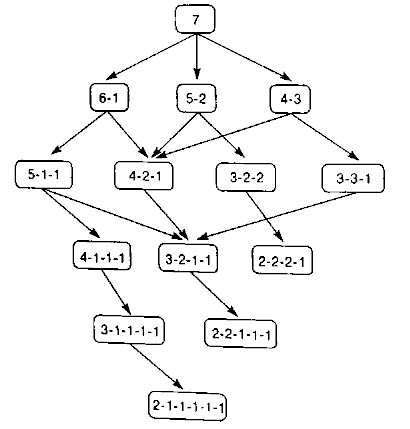
Рис.7. Граф игры «ним» для 7 фишек ■

Пример 8. Игра «Две кучки». Имеется две кучки, в каждой из которых имеется 4 фишки. Игрок может сделать один из следующих трёх ходов:

1. Забрать одну фишку из 1-ой кучки.

2. Забрать одну фишку из 2-ой кучки.

3. Забрать по одной фишке из обеих кучек.

Два игрока делают ходы по очереди. Проигрывает игрок, который забирает последнюю фишку. Разумеется, если в процессе игры в одной из кучек не осталось фишек, то у игроков из трёх хо-дов остаётся только один: забрать одну фишку из той кучки, в которой они ещё остались.

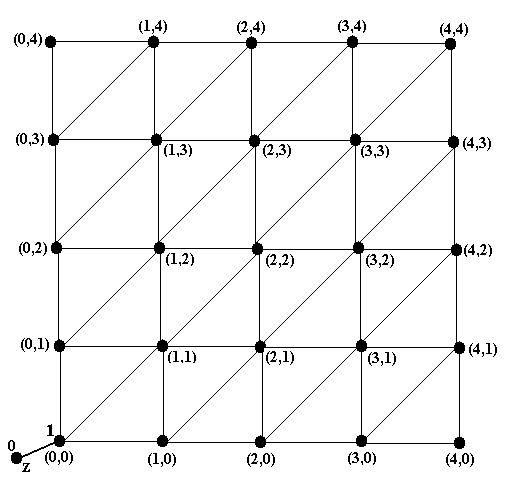
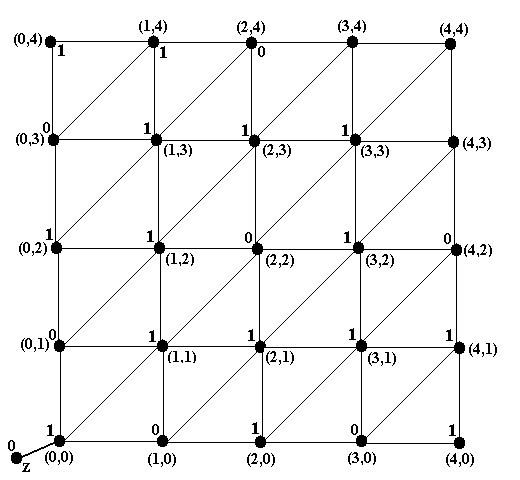
Рассматриваемую игру можно представить графом, показанным на рис.8. Как и в преды-дущем примере, вершины соответствуют всем возможным позициям в игре, а дуги – ходам, т.е. переходам между позициями. Пара чисел в скобках у вершины указывает на число предметов в 1-й и 2-й кучке в соответствующей позиции. Игра начинается в вершине (4,4) и заканчивается в вершине (0,0). Из каждой вершины есть три перехода – налево (взят предмет из 1-й кучки), вниз (взят предмет из 2-й кучки) и по диагонали (взяты по одному предмету из обеих кучек).

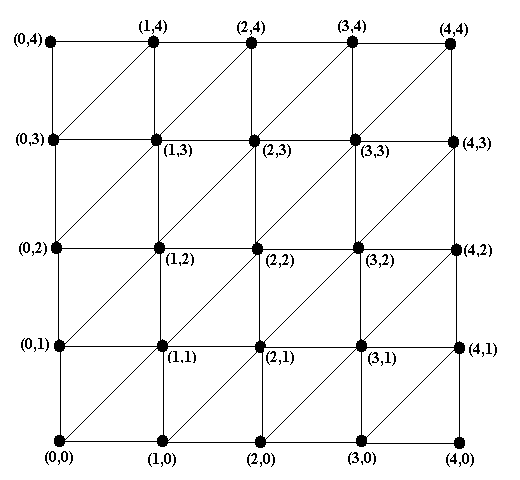
Рис.8. Граф игры «две кучки» ■

Дадим теперь достаточно общее описание игр рассматриваемого типа. Имеется ациклич-ный (т.е. не содержащий циклов) граф. Одна вершина объявляется начальной. Одна (отличная от начальной) вершина объявляется финальной. Предполагается, что финальная вершина явля-ется единственной вершиной в графе, из которой не выходит ни одной дуги. Игра состоит в том, что игроки по очереди переходят из вершины в вершину по дугам графа, причём 1-ая вер-шина обязательно должна быть начальной. При указанном предположении через конечное чис-ло ходов один из игроков обязательно попадает в финальную вершину, на чём игра и заканчи-вается. Игрок, попавший в финальную вершину, считается победителем. Обычно (см. примеры 7 и 8) вершины графа интерпретируются как позиции в игре, что и позволило дать таким играм естественное название «позиционные».

На первый взгляд, некоторые условия могут показаться слишком ограничительными. В игре «ним» имеется не одна, а три финальных вершины. В ней игрок, попавший в любую фи-нальную вершину, действительно является победителем, поскольку другой игрок не может хо-дить. В то же время в игре «две кучки» игрок, попавший в единственную финальную вершину (0,0), является проигравшим, так как он взял последнюю фишку. Но оказывается, что все эти ситуации просто сводятся к описанной. Рассмотрим эти ситуации по отдельности.

1. Имеется несколько финальных вершин. Добавим к графу одну вершину z и проведём дуги из каждой финальной вершины в вершину z. Вершина z будет единственной финальной вершиной в новом графе. Если в исходной игре попадание в любую финальную вершину было проигрышем, то в новой игре попадание в новую единственную финальную вершину стало вы-игрышем. Наоборот, если в исходной игре попадание в любую финальную вершину было выиг-рышем, то в новой игре попадание в новую единственную финальную вершину стало проигры-шем. Понятно, что суть игры совершенно не изменилась, поскольку в новую вершину попадает всегда не тот игрок, который попал в любую из исходных финальных вершин, а как раз другой. Таким образом, всегда можно рассматривать эквивалентную игру с одним финальным состоя-нием.

2. Игрок, попавший в единственную финальную вершину, считается проигравшим. В этом случае также добавляется одна новая финальная вершина z, в которую ведёт одна дуга из старой финальной вершины. Очевидно, что игрок, не попавший в старую финальную верши-ну, попадает в новую финальную вершину, т.е. является победителем в новой игре. Поэтому проигравшим в новой игре игроком является тот же игрок, который был проигравшим и в ста-рой игре, т.е. новая и старая игра эквивалентны.

Таким образом, мы приходим к описанной выше модели позиционной игры, победитель которой – это игрок, попавший в единственную финальную вершину.

Опишем алгоритм, позволяющий одному из игроков всегда выигрывать в позиционной игре. Суть его в том, что вершинам графа (т.е. позициям игры) приписываются метки 0 или 1. В зависимости от того, какую метку получает начальная вершина, выигрывает начинающий или делающий следующий за ним ход игрок.

Алгоритм 2. Расстановка меток у вершин графа игры.

1. Инициализация. Сопоставим финальной вершине метку 0.

В поочерёдных позиционных играх, в которых ноль стоит в финальной позиции, все остальные нули и единицы ставятся по следующим правилам:

А. Пометим 1-ей все вершины, откуда за один ход можно попасть в вершины с меткой 0.

Б. Пометим 0-ём все вершины, откуда за один ход можно попасть только в вершины с меткой 1.

В. Чередуем шаги А и Б до тех пор, пока не окажется помеченной начальная вершина.

Стоп (алгоритм прекращает работу).

Дадим необходимые пояснения. Тот игрок, который каким бы то ни было образом оказал-ся в вершине с меткой 1, может гарантированно выиграть, потому что он всегда может из 1 пе-рейти в 0, откуда другой игрок может перейти только в 1 и т.д. Таким образом, другой игрок всегда будет попадать в вершины с меткой 1, и поэтому он никогда не придёт в финальную вершину с меткой 0. Следовательно, если в начальной вершине стоит метка 1, то начинающий игрок выигрывает, а если стоит 0, то он проигрывает ■

Пример 9. Рассмотрим игру из примера 8 и проиллюстрируем на этом примере работу ал-горитма 2. Прежде всего надо добавить новую финальную вершину z, поскольку в исходной иг-ре из примера 8 игрок, попавший в финальную вершину, проигрывает. Новый граф показан на рисунке 9a. У вершины z, в соответствии с шагом 1 алгоритма 2, поставлена метка 0.

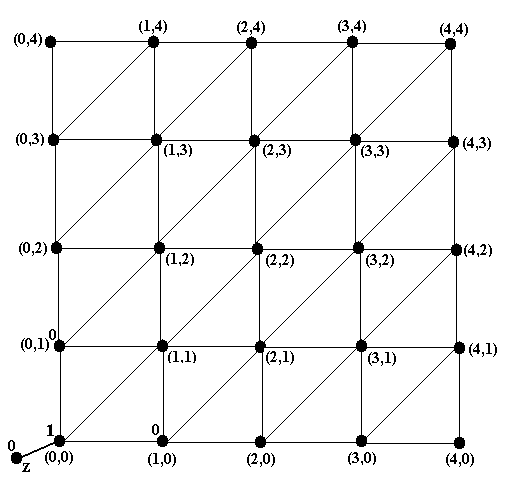
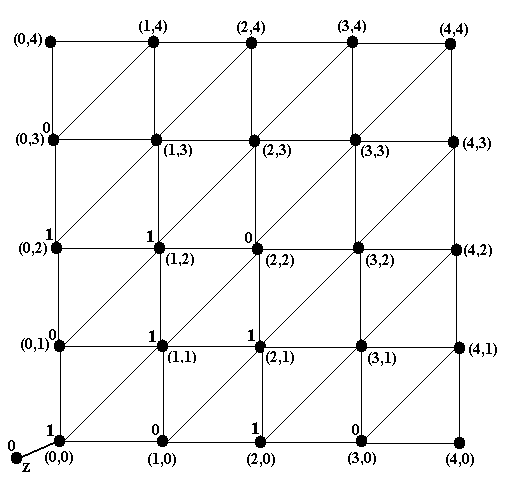
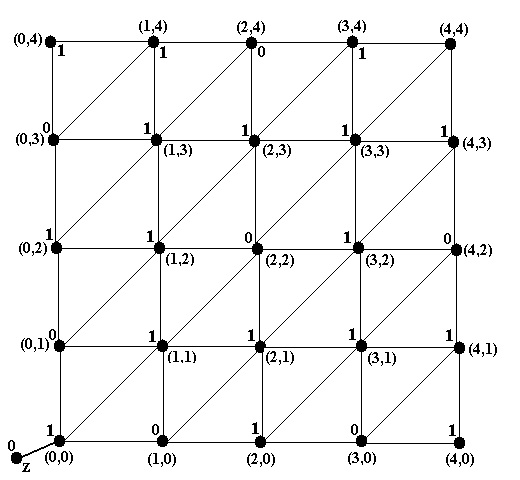
Выполняя шаг А, ставим метку 1 у вершины (0,0), откуда можно попасть в вершину z, у которой уже стоит метка 1 (см. рис.9b). Выполняя шаг 2, ставим метки 0 у вершин (0,1) и (1,0), откуда можно попасть только в вершину (0,0), у которой уже стоит метка 1 (см. рис.9c). Далее, выполняя 2-ой раз шаг А, ставим метку 1 у 5 вершин: (0,2), (1,2), (1,1), (2,1), (2,0), из каждой из которых можно попасть в вершины (0,1) или (1,0), уже помеченных 0-ём (рис.9d). Выполняя 2-ой раз шаг Б, ставим метку 0 у вершин (0,3), (2,2) и (3,0), из которых можно попасть только в одну из вершин (0,2), (1,2), (1,1), (2,1), (2,0), которые уже получили метку 1 (рис.9e).

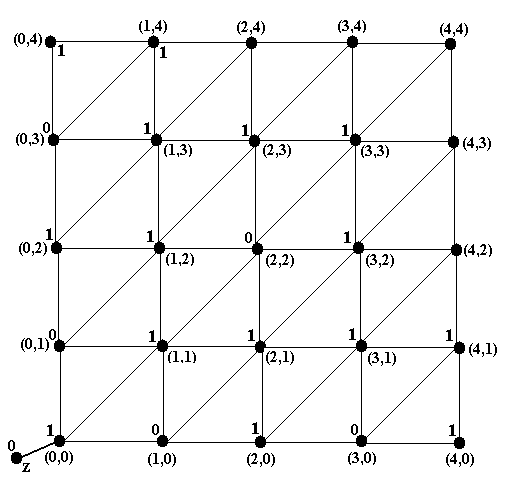
Дальнейшие аналогичные шаги представлены на рис.9f и 9g, а затем на рис.9h и 9i. При выполнении шага Б начальная вершина (4,4) получает метку 0. Это означает, что начинающий игрок в данной игре проигрывает, если другой игрок будет каждый раз из вершины с меткой 1 переходить в вершину с меткой 0, в соответствии с пояснениями к алгоритму 2.

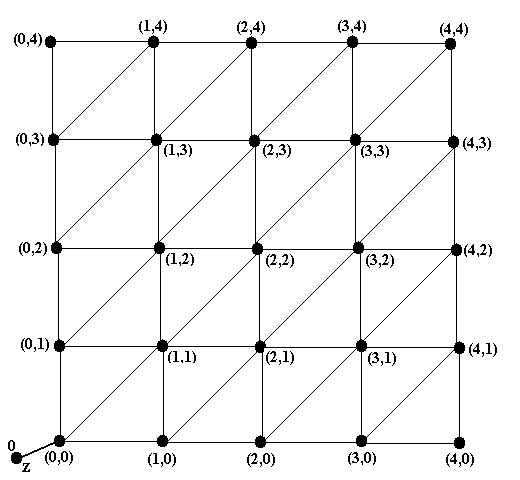
Рис.9a. Новый граф и его инициализация

Рис.9b. Шаг А-1

Рис.9c. Шаг Б-1

Рис.9d. Шаг А-2

Рис.9e. Шаг Б-2

Рис.9f. Шаг А-3

Рис.9g. Шаг Б-3

Рис.9h. Шаг А-4

Рис.9i. Шаг Б-4

■

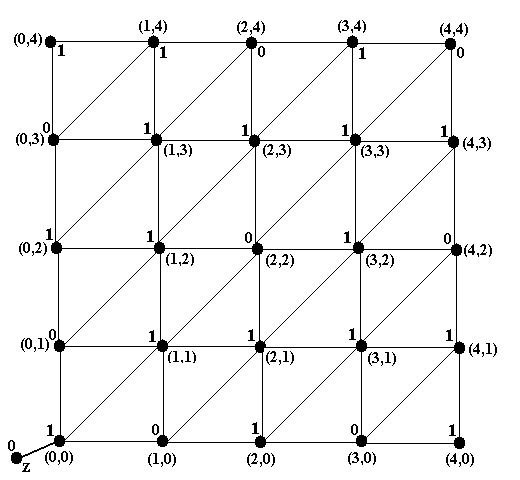
Пример 10. Рассмотрим модификацию игру «Две кучки» с графом на рис.10. От игры из

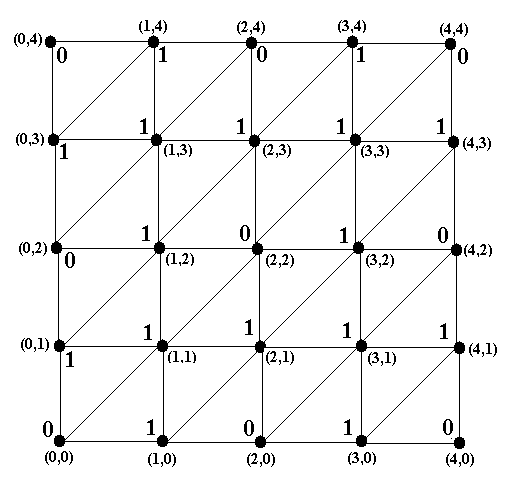
Рис.10. Граф модифицированной игры «Две кучки»

из примеров 8 и 9 она отличается только тем, что игрок, взявший последнюю фишку, выигрыва-ет. Это означает, что вершина (0,0) является финальной вершиной и в соответствии с шагом 1 алгоритма 2 она получает метку 0. Все метки, поставленные в соответствии с алгоритмом 2, показаны на рис.10. У всех вершин, кроме самого левого столбца и самой нижней строки, все метки на рисунках 10 и 9i полностью совпадают. В частности, совпадают и метки у начальной вершины (в обоих случаях 0). Поэтому в модифицированной игре «Две кучки» начинающий также проигрывает, как и в исходной игре. Это означает, что симметрия при изменении опреде-ления победителя отсутствует ■

Задание 3. Найти решение в играх «Две кучки», заданных в следующей таблице:

№	Число фи-шек в 1-ой кучке	Число фи-шек во 2-ой кучке	Игрок, взявший последнюю фишку
01	3	4	проигрывает
02	3	4	выигрывает
03	3	5	проигрывает
04	3	5	выигрывает
05	3	6	проигрывает
06	3	6	выигрывает
07	4	5	проигрывает
08	4	5	выигрывает
09	4	6	проигрывает
10	4	6	выигрывает
11	5	5	проигрывает
12	5	5	выигрывает
13	5	6	проигрывает
14	5	6	выигрывает
15	6	6	проигрывает
16	6	6	выигрывает

Ответ должен быть дан в виде графа с помеченными вершинами, как на рис.9i и 10. Должно быть указано, какой игрок (начинающий или следующий) выигрывает ■