Расчёт с помощью таблиц, выполненных средствами Microsoft Excel.
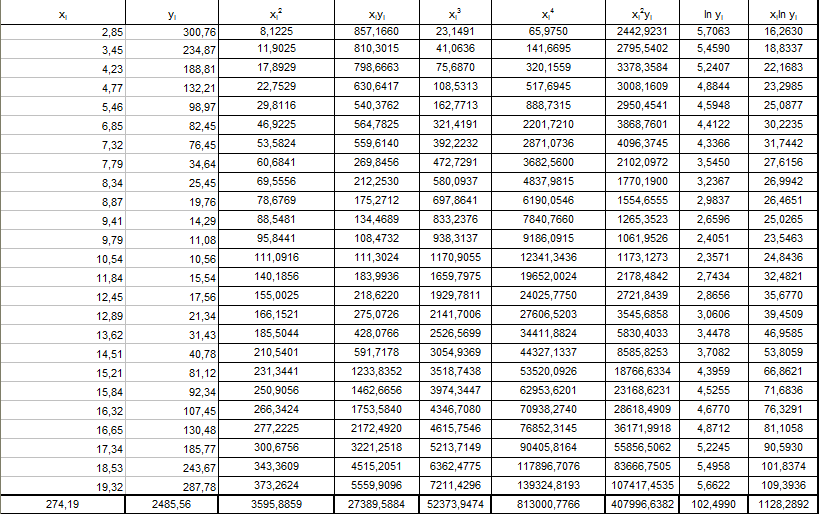
Для проведения расчётов, данные целесообразно расположить в виде таблицы 1, используя средства табличного процессора Microsoft Excel.
Табл. 1.
Аппроксимируем
функцию
линейной функцией . Для определения
коэффициентов
и
воспользуемся
системой (4). Используя итоговые суммы
таблицы 2, расположенные в ячейках A27,
B27,
C27
и D27,
запишем систему (4) в виде
(11)
решив
которую, получим
и
.
Систему решали методом Крамера. Суть которого состоит в следующем. Рассмотрим систему n алгебраических линейных уравнений с n неизвестными:
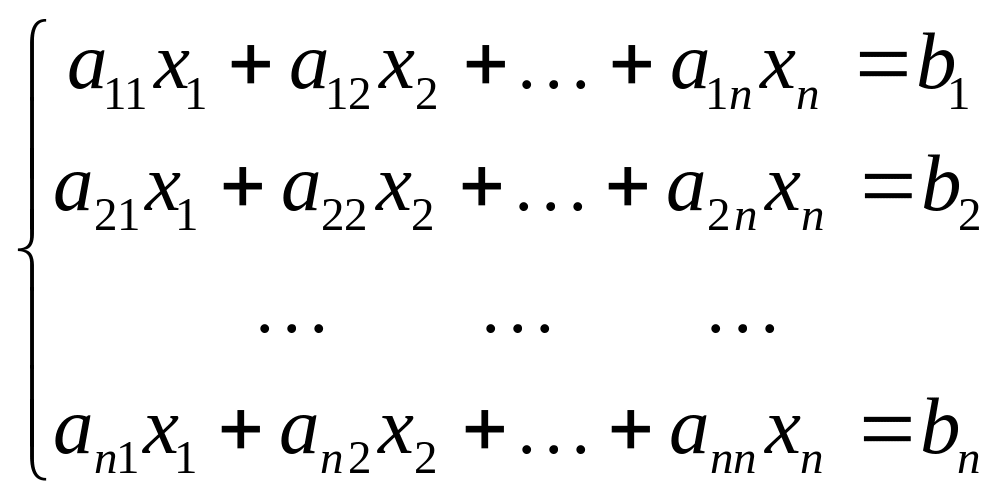(12)
Определителем системы называется определитель матрицы системы:
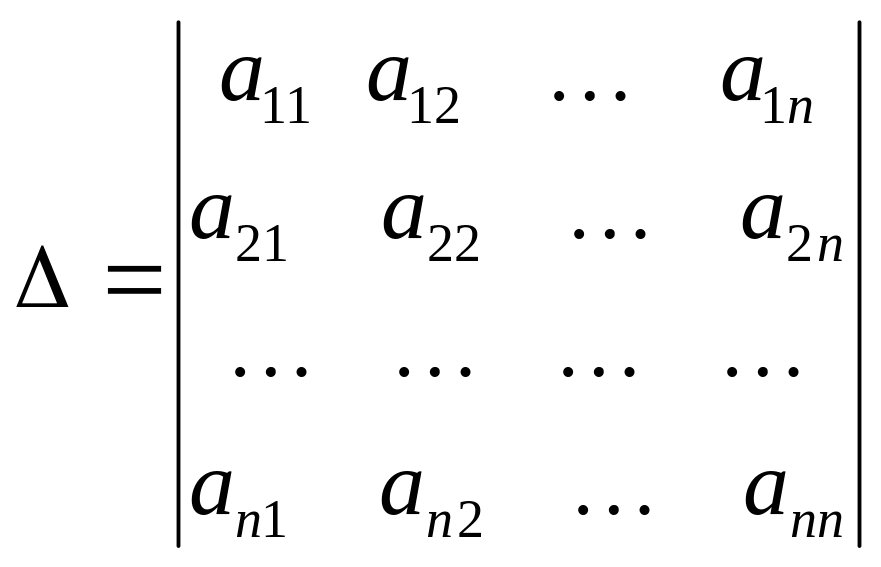(13)
Обозначим
-
определитель, который получится из
определителя системы Δ заменой j-го
столбца на столбец
(14)
Таким образом, линейная аппроксимация имеет вид
(15)
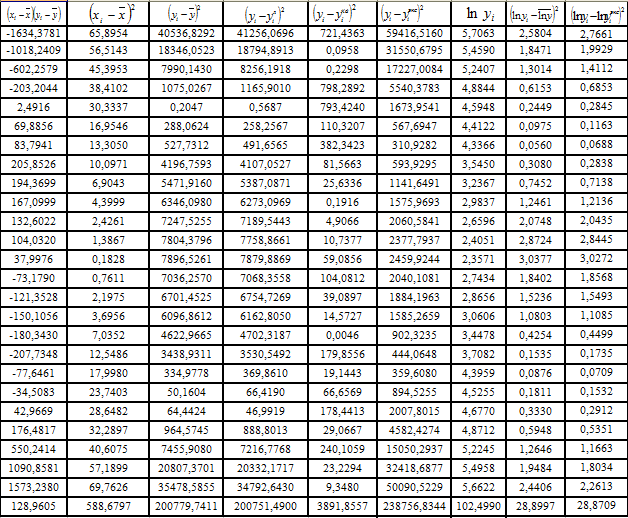
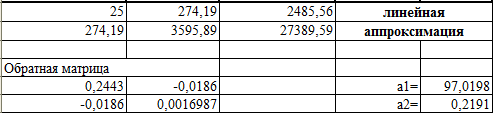
Решение системы (11) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 2.
Таблица 2.
Далее
аппроксимируем функцию
квадратичной функцией
.
Для определения коэффициентов a1,
a2
и a3
воспользуемся системой (5). Используя
итоговые суммы таблицы 1, расположенные
в ячейках A27, B27,
C27
, D27,
E27,
F27,
G27
запишем систему (5) в виде
(16)
решив которую, получим
,
и
Таким образом, квадратичная аппроксимация имеет вид
(17)
Решение системы (16) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 3.
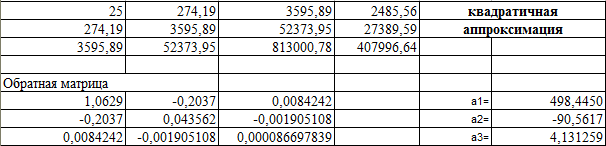Таблица
3.
Теперь
аппроксимируем функцию
экспоненциальной функцией
.
Для определения коэффициентов
и
прологарифмируем значения
и, используя итоговые суммы таблицы 2,
расположенные в ячейках A27, C27,
H27
и I27,
получим систему
(18)
где
.
Решив
систему (18), получим
и
.
После
потенцирования получим
.
Таким образом, экспоненциальная аппроксимация имеет вид
(19)
Решение системы (18) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 4.
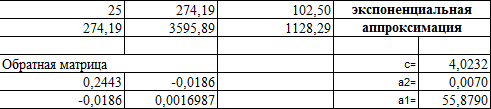
Таблица 4.
Вычислим
среднее арифметическое
и
по формулам:
;
.
Результаты расчета и средствами Microsoft Excel представлены в таблице 5.
Таблица 5.
Для того, чтобы рассчитать коэффициент корреляции и коэффициент детерминированности данные целесообразно расположить в виде таблицы 6, которая является продолжением таблицы 1.
Таблица 6.
Теперь проведем расчеты коэффициента корреляции по формуле (8) (только для линейной аппроксимации) и коэффициента детерминированности по формуле (10). Результаты расчетов средствами Microsoft Excel представлены в таблице 7.
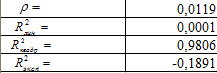
Таблица 7.
Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.