Решение типового примера.

Пример 7. Доказать, что векторы образуют базис. Разложить вектор по этому базису.

Если определитель, составленный из координат этих векторов, не равен нулю, то векторы образуют базис.

В нашем случае:

.

Следовательно, векторы образуют базис.

Разложим вектор по базису векторов . Для этого представим вектор в виде линейной комбинации векторов :

.

Подставим координаты векторов :

.

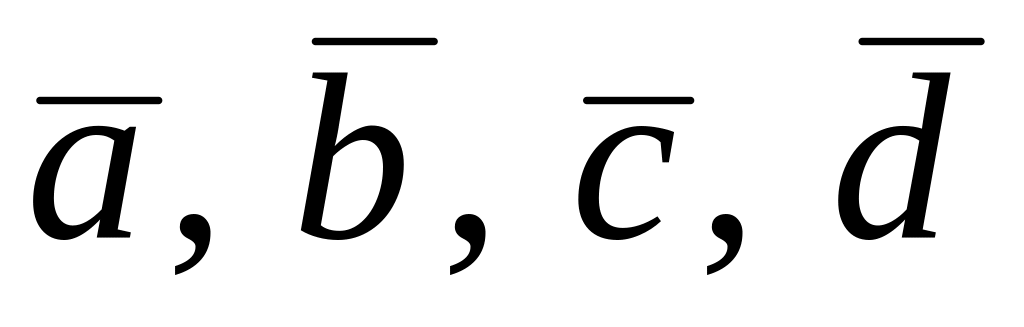Данная запись равносильна системе:

Найдём . Для этого решим данную систему методом Гаусса:

~ ~ ~

~ ~ ~ ~

~ .

Последняя матрица эквивалентна системе:

Тогда

Следовательно,

.

Литература:

1. Минорский В.П. Сборник задач по высшей математике – М.: Наука, 2003.

2. Шипачёв В.С. Задачник по высшей математике: Учеб. пособие для вузов. – 2-е изд., испр. – М.: Высш. шк., 1998.

3. Математика для экономистов: в 6 т. – М.: ИНФРА-М, 2000. Т.1: Идельсон А.В., Блюмкина И.А. Аналитическая геометрия. Линейная алгебра. Учеб. пособие /под ред. Л.П. Гаштольда, В.Г. Дмитриева, А.Ф. Тарасюка.

4. Клетеник Д.В. Сборник задач по аналитической геометрии: Учеб. пособие для втузов. – М.: Наука, 2003.

24