
2.6.1 Алгоритм пошуку у ширину
Алгоритм пошуку у ширину – один із базових алгоритмів, який є основою для багатьох інших алгоритмів на графах (наприклад алгоритм Дейкстри).
Допустимо, що заданий граф .і фіксована початкова вершина . Алгоритм пошуку у ширину знаходить всі доступні із вершини у порядку збільшення віддалі від . Віддалю між будь-якими двома вершинами графа є довжина (число ребер) найкоротшого шляху. У процесі пошуку із графа виокремлюється його частина, яка називається «» з коренем . Для кожної із вершин, які належать дереву пошуку у ширину, шлях із кореня у дереві буде найкоротшим. Алгоритм може застосовуватись як до неорієнтованих, так і до орієнтованих графів.
Для наочності вважатимемо, що у процесі роботи алгоритму вершини графа можуть бути білими, сірими і чорними. Спочатку всі вершини білі, але в процесі роботи алгоритму біла вершина може стати сірою, а сіра – чорною (але не навпаки). Зустрівши нову вершину (білу або сіру), алгоритм її зафарбовує. Це будуть ті вершини, які уже виявлені алгоритмом. Різниця між сірими і чорними вершинами використовується алгоритмом для керування порядком обходу: сірі вершини утворюють лінію «фронту», а чорні – «тил». Точніше, якщо , то і чорна, то - сіра або чорна.
Спочатку дерево пошуку вміщує тільки один корінь – початкову вершину . Як тільки алгоритм виявляє нову білу вершину , яка є суміжною з раніше знайденою вершиною , вершина разом з ребром долучається до дерева пошуку, стаючи дитиною вершини , а буде родичем вершини . Кожна вершина виявляється тільки один раз, так що двох родичів у неї не може бути. Поняття предка і нащадка визначається як завжди (потомки – це діти, діти дітей і т. д.). Рухаючись від кореня до вершина дерева пошуку, знаходимо всіх предків.
Наведена нижче процедура BFS
(breadth-first search - пошук у ширину) використовує
подання графа
списком суміжних вершин. Для кожної
вершини графа
додатково зберігається її колір
![]() і її попередник
і її попередник
![]() .
Якщо попередника немає (наприклад,
.
Якщо попередника немає (наприклад,
![]() або вершина
ще не виявлена), то
або вершина
ще не виявлена), то
![]() .
Віддаль від
до
записується в поле
.
Віддаль від
до
записується в поле
![]() Процедура використовує також чергу
Процедура використовує також чергу
![]() для зберігання множини сірих вершин.
для зберігання множини сірих вершин.
BFS(G,s)
1
for (для кожної вершини
![]() )
)
2 color(v)=білий
3
![]()
4
![]()
5 end for
6 color(s)=сірий
7
![]()
8
![]()
9 Q={s}
10
while
![]()
11 v=head(Q)
12
for (для) всіх
![]()
13 if color(w)=білий
14 then color(w)=сірий
15 d(w)=d(w)+1
16
![]()
17 Enqueue(Q,w)
18 end if
19 end for
20 Dequeue(Q,w)
21 color(v)=чорний
22 end while
Процедура
BFS використовує
операцію добавляння вершини до черги
і вона позначається як Enqueue
та операцію видалення вершини із черги
- Dequeue.
Тут використано наступне провило: перший
прийшов – першим обслужений. Черга має
голову
(head) і
хвіст
(tail). Вершина, що добавляється до черги
стає у хвіст, а вершина, що вилучається
із черги, знаходиться у її голові. На
рис. 2.12 показано як можна реалізувати
чергу, яка вміщує не більше ніж
![]() елемент, на базі масиву
елемент, на базі масиву
![]()
![]() .
Зберігається індекс
.
Зберігається індекс
![]() - голова черги та
- голова черги та
![]() - індекс вільної комірки, в яку буде
поміщений наступний елемент, що
долучається до черги. Черга складається
із елементів масиву з номерами
,
- індекс вільної комірки, в яку буде
поміщений наступний елемент, що
долучається до черги. Черга складається
із елементів масиву з номерами
,
![]() ,
…,
,
…,
![]() .
Якщо
=
,
то черга пуста. На початку роботи
процедури маємо
=
=1.
.
Якщо
=
,
то черга пуста. На початку роботи
процедури маємо
=
=1.
Нижче наведені процедури добавлення елемента (вершини) до черги Enqueue(Q,w) та вилучення елемента (вершини) вершини із черги Dequeue.
Enqueue(Q,w)
1 Q(tail(Q))=w
2 if tail(Q)=length(Q)
3 then tail(Q)=1
4 else tail (Q)= tail (Q)+1
5 end if
Dequeue(Q,w)
1 w= Q(tail(Q))
2 if head(Q)=length(Q)
3 then head(Q)=1
4 else head(Q)=head(Q)+1
5 end if
6 return w
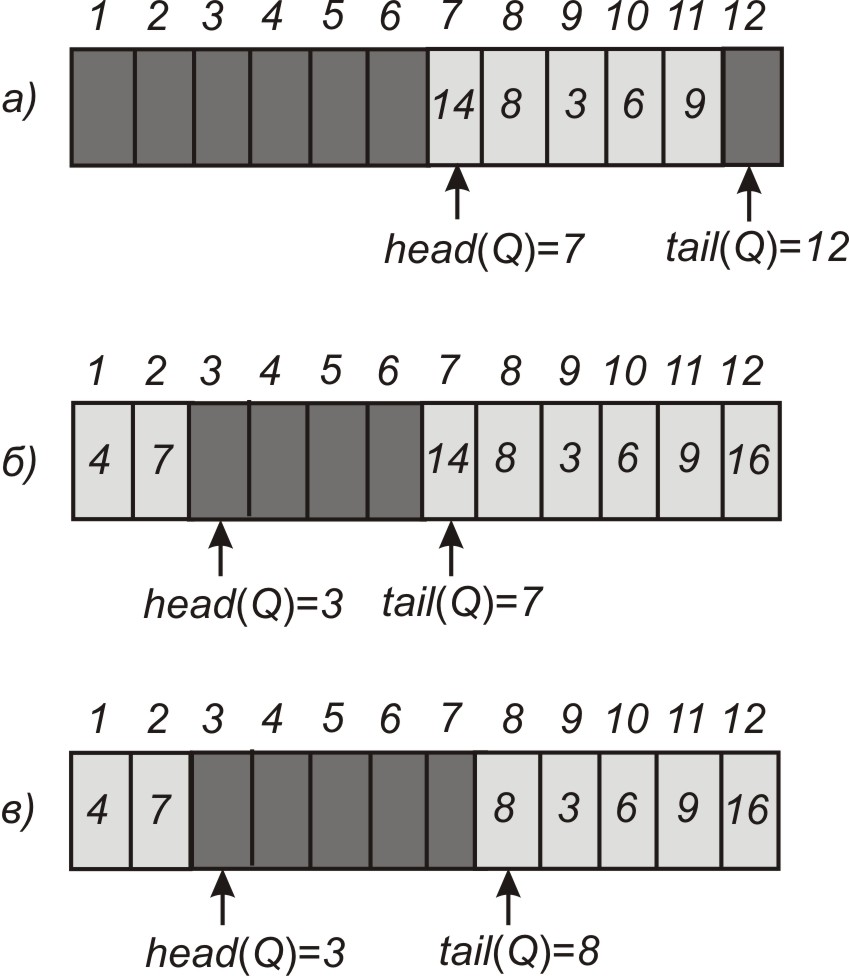
Рисунок 2.12 – Черга, що реалізована на базі масиву :
а)
світло-сірі клітинки заняті елементами
черги. В черзі знаходиться 5 елементів
(позиції
![]() );
б) черга після виконання процедур
Enqueue(Q,16),
Enqueue(Q,4)і
Enqueue(Q,7);
в) черга після виконання процедури
Dequeue(Q),
яка повертає значення 16. Новою головою
черги стає число 8
);
б) черга після виконання процедур
Enqueue(Q,16),
Enqueue(Q,4)і
Enqueue(Q,7);
в) черга після виконання процедури
Dequeue(Q),
яка повертає значення 16. Новою головою
черги стає число 8
Повернемось тепер до основної
процедури BFS.
У рядках 1 – 4 вершини стають білими, а
всі значення
![]() приймають значення
і родичі всіх вершин об’являються
NIL.Рядки
6 – 9 фарбують вершини
у білий колір і виконують пов’язані з
цим дії: у рядку 7 віддаль
приймають значення
і родичі всіх вершин об’являються
NIL.Рядки
6 – 9 фарбують вершини
у білий колір і виконують пов’язані з
цим дії: у рядку 7 віддаль
![]() об’являється рівною нулю, а в рядку 8
говориться, що родичів у
немає. І нарешті у рядку 9 вершина
стає у чергу
і з цього моменту черга
буде вміщувати сірі вершини і тільки
їх.
об’являється рівною нулю, а в рядку 8
говориться, що родичів у
немає. І нарешті у рядку 9 вершина
стає у чергу
і з цього моменту черга
буде вміщувати сірі вершини і тільки
їх.
Основний цикл програми (рядки
10 – 22) виконується поки черга не пуста,
тобто існують сірі вершини. У лінійці
11 така вершина поміщається у
.
Цикл for
у рядках 12 – 19
проглядає всі суміжні з нею вершини.
Виявивши серед них білу вершину ,
процедура BFS
робить її сірою (рядок 14), об’являє її
родичів (рядок 16) і встановлюємо віддаль
рівною
![]() (рядок15). І нарешті, ця вершина добавляється
у хвіст черги (рядок 17). Після цього вже
можна видалити вершину
із черги
,
перефарбувавши цю вершину у чорний
колір (рядки 20 – 21).
(рядок15). І нарешті, ця вершина добавляється
у хвіст черги (рядок 17). Після цього вже
можна видалити вершину
із черги
,
перефарбувавши цю вершину у чорний
колір (рядки 20 – 21).
Рис. 2.13 наочно демонструє
виконання процедури
BFS для неорієнтованого
графа
,
у якого
![]() ,
,
![]() .
.

Рисунок 2.13 – Використання процедури BFS для неорієнтованого графа
Вершини дерева, що формуються, показані сірим. Всередині кожної вершини вказано значення . Показано стан черги перед кожним повторенням циклу у рядках 10 – 22. Поряд з елементами черги вказані віддалі від кореня дерева.
