Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра КТРС

Лабораторная работа №1

«Проектирование аналоговых отражающих фазовращателей с помощью ЭВМ »

Новосибирск 2005 г.

Лабораторная работа № 1

Проектирование аналоговых отражающих фазовращателей с помощью ЭВМ.

1. Цель работы

Изучение метола точного синтеза реактивных двухполюсников с линейной ФЧХ коэффициента отражения и методики проектирования аналогового отражательного фазовращателя (АОФВ) на его основе. Проектирование АОФВ на варикапах с использованием ЭВМ и учетом реальных параметров радиоэлементов. Исследование амплитудно- и фазочастотных характеристик АОФВ методами математического модели­рования в САПР «OrCAD 9.2» для достижения за­данных характеристик АОФВ. Приобретение практических навыков схе­мотехнического моделирования на ЭВМ.

2. Основные сведения

2.1. Общие положения

Назначение фазовращателя (ФВ) - регулирование фазы колебаний сигналов в различных радиоэлектронных устройствах - определяет совокупность предъявляемых к нему требований. Это диапазон рабо­чих частот - , число различных фазовых состояний или мини­мальный дискрет изменения управляемого фазового сдвига (УФС), максимальная погрешность установки и поддержания УФС в диапазоне рабочих частот - , максимально допустимый уровень потерь - и изменение потерь при перестройке УФС - (паразитная амплитудная модуляция - ПАМ), пропускная мощность - , время переключения УФС - и др.

По способу управления фазой ФВ могут быть дискретными или аналоговыми (плавными). В дискретных ФВ наибольшее применение находят p-i-n диоды в качестве управляющих элементов (УЭ), а в аналоговых - диоды с управляемой емкостью p-n перехода - вари­капы.

По принципу действия ФВ разделяют на проходные и отражатель­ные. Проходной фазовращатель - это четырехполюсник с регулируе­мой фазой коэффициента передачи. Отражательные ФВ - это двух­полюсники с регулируемой Фазой коэффициента отражения. По зави­симости УФС от частоты ФВ можно разделить на дисперсионные и не­дисперсионные. В дисперсионных ФВ УФС в рабочей полосе частот не зависит от частоты, является лишь функцией управляющего воздей­ствия. В недисперсионных ФВ фазовый сдвиг линейно зависит от частоты.

В данной работе рассматриваются широкополосные аналоговые от­ражательные фазовращатели на варикапах с дисперсионной ФЧХ.

2.2. Синтез аофв с линейной фазочастотной характеристикой

А ОФВ представляет собой двухполюсник с регулируемой фазой коэффициента отражения - (рис.1). Проектирование таких ФВ сводится к задаче синтеза двухполюсника с требуемым видом амплитудной и фазочастотной характеристик (АЧХ и ФЧХ) коэф­фициента отражения. Широкополос­ный АОФВ, для которого потерями в элементах можно пренебречь из-за их малости, можно предста­вить в виде реактивного двухпо­люсника. Влияние потерь в элемен­тах на характеристики АОФВ определяется при его анализе.

Изображение по Лапласу функции входного сопротивления реак­тивного двухполюсника яв­ляется нечетной функцией комплексной частоты . Нули и полюсы лежат на мнимой оси, они являются простыми и взаимно чередуются. Следовательно, будет дробно-рациональной функцией, представляемой в виде отно­шения полинома по нечетным степеням р и полиному по четным степеням (либо наоборот).

(1)

где

.

- полиномы по четным степеням .

Коэффициент отражения АОФВ - как реактивного двухполюсни­ка, подключенного к генератору с выходным сопротивлением , с учётом (1)

, (2)

где

- полином Гурвица степени ;

- аргумент полинома Гурвица.

Из (2) следует, что модуль коэффициента отражения не зависит от частоты и всегда равен единице; -фаза коэф­фициента отражения равна с обратным знаком удвоенному значению аргумента полинома . Максимальный размах фазочастотной ха­рактеристики коэффициента отражения АОФВ определяется порядком цепи, т.е. числом реактивных элементов - п и равен - . В про­цессе регулирования АОФВ изменением величины реактивных эле­ментов (емкостей варикапов) порядок цепи не изменяется, следова­тельно, не изменяется и размах ее ФЧХ. Это означает, что необхо­димую величину управляемого фазового сдвига - в рабочей по­лосе частот можно получить только за счет смещения влево или вправо по оси частот (рис.2). При этом максимально достижи­мая величина не может превышать размаха и также зави­сит от порядка цепи АОФВ.

АОФ с постоянной абсолютной величиной в рабочей поло­се частот удобно реализовать в виде перестраиваемого по частоте двухполюсника с линейной ФЧХ (рис.2). В этом случае синтез АОФВ сводится к синтезу реактивного двухполюсника с линейной и неизменяющимся наклоном при его перестройке. Для синте­за двухполюсника с линейной необходимо определить аппрок­симирующий полином Гурвица , который имеет линейную зависимость аргумента (фазы) от частоты в заданном диапазоне частот.

Из (1) и (2) следует, что

(3)

Последнее означает, что фаза коэффициента отражения реактив­ного двухполюсника выражается через нормированное значение вход­ного сопротивления следующий образом:

(4)

Требование линейности ФЧХ означает, что при в задан­ной полосе частот должно удовлетворяться равенство

.

Отсюда

.

Функцию , а значит, и можно разложить в цеп­ную дробь следующего вида:

(5)

,

после свертывания которой получается дробно-рациональная функция вида (1), для которой полином Гурвица известен под назва­нием полинома Бесселя степени .

, (6)

где

;

.

Аргумент (фаза) такого комплексного полинома Бессьля- максимально плоско приближается к линейной зависи­мости. Отклонение от линейной зависимости - оп­ределяется выражением (рис.3.)

(7)

Заметим, что максимальное отклонение согласно (2) будет вдвое выше величины .

Входное сопротивление двухполюсника в виде цепной дроби легко реализуется в виде двухполюсника лестничной структуры (реализа­ция по Кауэру). Одна из возможных реализаций такой цепи показана на рис.4. Такой двухполюсник имеет линейную с погрешностью 2 ФЧХ коэффициента отрешения, а нормированные значения его реак­тивных элементов - g_i определяются из (5) как

(8)

Двухполюсник (рис.4) с линейной ФЧХ можно применить в ка­честве НЧ прототипа для расчета АОФВ. Для реализации полосовой цепи из НЧ прототипа применим частотное преобразование вида

которое называется реактансным. Это частотное преобразование трансфор-мирует интервал частот НЧ прототипа по шкале нормированных

частот в полосу по шкале действительных круговых частот, полосовой цепи . При таком частотном преобразовании ФЧХ полосовой цепи искажается и отклоняется от линейной. Максимум отклонения ФЧХ от линейной получается на центральной частоте.

Его значение

, (9)

где – угол наклона ФЧХ .

При реактансном частотном преобразовании в LС - цепях проис­ходит одновременное преобразование индуктивностей L в последо­вательные контуры с индуктивностью L₁ и емкостью С₁, равными

, (10а)

и емкостей С – в параллельные контуры

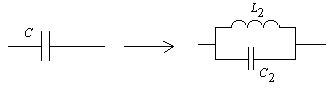
с индуктивностью L₂ и емкостью C₂ равными:

(10б)

и полосой частот, в которой обеспечивается линейная ФЧХ (рис. 2)

(11)

где - диапазон перестройки резонатора АОФВ;

- полоса рабочих частот АОФВ;

(12)

- граничная частота нормированного полинома Бесселя степени n;

- заданная максимальная величина управляемого фазового сдвига

АОФВ.

НЧ прототипы используются для упрощения расчета, который сводится к определению элементов НЧ прототипа по ранее проведенной методике. После расчета НЧ прототипа схема преобразуется к полосовому виду. Прямое преобразование схемы НЧ прототип (рис.4) с использованием (10) приводит к схеме полосового двухполюсника в реальном масштабе частот. Такая реализация неудобна для перестраиваемых цепей, какой является АОФВ, так как требует использования неодинаковых управляющих элементов.

Значительно удобнее схему АОФВ - полосового перестраиваемого реактивного двухполюсника реализовать в виде одинаковых перестраиваемых резонаторов, связанных между собой элементами свези - инверторами сопротивления (или проводимости). Такая реализация позволяет использовать в перестраиваемых двухполюсниках одинаковые перестраиваемые элементы. Инверторы сопротивления - К (или инверторы проводимости - У) можно определить через значения элементов НЧ прототипа и параметры крутизны реактивного сопротивле­ния (или проводимости) используемых резонаторов.

Для схем АОВФ, содержащих инверторы сопротивления и одинако­вые последовательные резонаторы (рис.5), параметры инверторов сопротивления определяются из выражений:

Для схемы рис.5.а

(13а)

Для схемы рис.5.б

(13б)

Для схемы АОФВ с линейной ФЧХ , содержащих инверторы прово­димости и одинаковые параллельные резонаторы (рис.6), параметры инверторов проводимости определяются из выражений:

для схемы рис.6а

(14а)

для схемы рис.6.б

(14б)

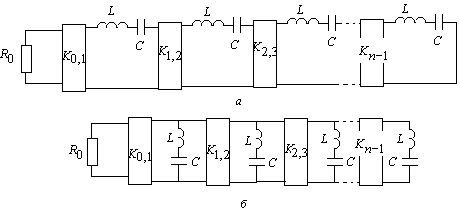
Рис.5. Схемы АОФВ с последовательными контурами и инверторами

сопротивления

Рис.6. Схемы АОФВ с параллельными контурами и инверторами проводимости

В этих выражениях

- средняя емкость варикапа;

- определяется из (16).

Приведенные выше соотношения являются точными для любой величины в том случае, если параметры инверторов не зависят от частоты, а резонаторы состоят из сосредоточенных элементов. Однако реально реализуемые инверторы частотно - зависимы, а резонаторы в диапазоне СВЧ выполняются с использованием отрезков линий передачи. Это приводит к возникновению погрешности в вычислениях по приведенным соотношениям, которая возрастает с расширением АОФВ. Для уточнения результатов расчета и учета потерь в элементах схемы на этапе анализа АОФВ, в случае необходимости, следует произвести корректировку параметров схемы АОФВ.