3.1.2 Проверка габаритов передачи по напряжениям изгиба
b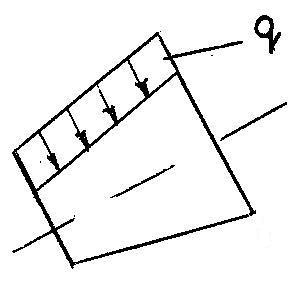
Рис. 3.3. Удельная нагрузка, действующая на зуб колеса
, (3.16)
где [σиз] – допустимое напряжение на изгиб для материала шестерни, см. уравнение (3.19).
Распределенная нагрузка q по профилю зуба распределяется равномерно, поэтому для расчета берем модуль mср.
0.85 – коэффициент, учитывающий, что нагрузочная способность конической передачи на 15% ниже, чем у цилиндрической передачи. Коэффициент формы зуба y определяется по табл. 2.3, определив Zпр.ш. Зуб шестерни находится в зацеплении чаще, чем зуб колеса.
;
(3.17)
;
(3.18)
отсюда mср
,
(3.19)
где kσ – коэффициент концентрации напряжения в ножке зуба; [n] – допустимый запас прочности.
По литературным рекомендациям:
kσ = 1.7 ÷ 1.8; [n] = 1.3 ÷ 1.8
3.2. Пример расчёта
Рассмотрим схему ИМ №9 (вариант 77), которая представляет собой двухступенчатый редуктор, состоящий из планетарной передачи с одинарным сателлитом и конической.
Пример расчета планетарной передачи уже рассматривался, поэтому, исходя из данных варианта 77, будем рассчитывать только коническую передачу.
Исходные данные:
Схема 9
Скорость V = 4 мм/с
24 – наружный диаметр резьбы, мм
2 – заходность резьбы (
5 – шаг резьбы ( , мм
Определив усилия, действующие в ИУ (см. 1 часть), и подобрав электродвигатель, можно приступить к определению габаритов заданной схемы и скомпоновать ИМ с запорной задвижкой.
В 1 части, предположим, был подобран асинхронный электродвигатель nоб = 750 об/мин с мощностью N = 1 кВт (Nр = 1,3 кВт).
Так как в схему ИМ входит планетарная одноступенчатая передача и коническая, то передаточное отношение может составлять:
.
По исходным данным определяем число оборотов выходного вала:
об/мин.
.
Передаточное отношение определяем в соответствии с данными табл. 3.3 часть 1. Для одноступенчатой передачи рекомендуется i = 7 ÷ 8, для конической – 1,5 ÷ 4. Принимаем iкон.пер = 4, тогда:
,
т.е. результатами предыдущего расчета воспользоваться не удаётся.
Не имея особых указаний на ограничение габаритов выбираем сравнительно недорогую углеродисто конструкционную сталь:
ст 45 – шестерня – 270 ед. твердости по Бринелю.
Колесо – 240 ед.
кг/см2.
Определяем углы начальных конусов, исходя из iкон.пер = 4:
;
.
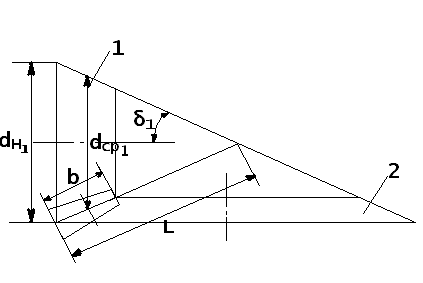
Рис. 3.4. Схема конической передачи (1 – шестерня, 2 – колесо)
L – основной геометрический размер конусной передачи.
Принимаем коэффициент ширины зуба колеса ψL и определяем L (см. лит источник).
об/мин.
Из условия прочности конической передачи по контактным напряжениям:
;
мм.
4. Определяем габариты конической передачи:
мм
мм. Принимаем b
= 25 мм.
ψm
= 15 (см.
лит),
.
;
.
Уточняем
мм.
;
мм.
Проверяем величину модулей по напряжениям изгиба:
;
.
мм.
мм.
Допустимое напряжение:
кг/см2.
Для ст45
кг/см2.
кг/см2.
об/мин.
;
кг·см.
у для приведенного числа зубьев:
Вычисляем σиз для шестерни, т.к. она чаще бывает в зацеплении:
кг/см2.
1944,9 < 2241
Неравенство осуществляется, но запас прочности на пределе, лучше модуль увеличить и пересчитать коническую передачу.