2.2.2. Определение усилий действующих в зацеплении.

В червячной передаче действуют силы (см. рис. 2.3):

1. ;

2. ;

3. .

Основной расчётной силой является P₂₁ⁿ, порядок её определения см. в п. 2.1.2.

Момент на колесе определяется по максимальному моменту на выходном валу задвижки, эту величину определяли при расчёте шпинделя (T_max при закрывании или T_max при открывании):

.

Тогда силы после определения M_к определяются следующим образом:

1. .

2. .

3. .

При наличии данных схемы 1 (вариант 11) можно определить вышеуказанные силовые факторы, действующие в червячной передаче ИМ.

Найденные габариты червячной передачи необходимо проверить по контактным напряжениям и по напряжениям изгиба (самостоятельно в п. 2.1.3).

3. Расчет конической передачи им (на примере схемы 9)

3.1. Теоретическая часть

3.1.1. Определение габаритов конической зубчатой передачи

Недостатки:

1. Сложность изготовления

2. Зуб конической передачи менее прочен, чем зуб прямозубой передачи на 15 %, поэтому при расчёте вводится коэффициент 0.85.

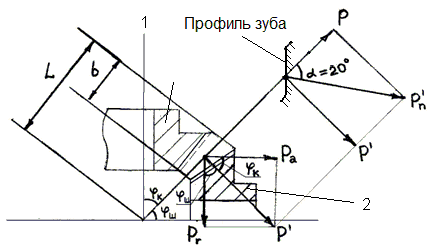
Рис. 3.1. Усилия, действующие в конической передаче (1 – колесо; 2 – шестерня)

P_r – радиальная сила; P_a – осевая сила; P_n’ – нормальная сила, перпендикулярная к профилю зуба; P – окружная сила; φ_к и φ_ш – углы зацепления колеса и шестерни; L – длина конуса, являющаяся основным габаритным размером; b – ширина зуба.

Как видно из рис. 3.1 зуб конической передачи различается по сечению в средней части и в торцевой, поэтому вводится понятие «модуль расчётный» (m_ср) и «модуль инструментальный» (m_s).

m_s – модуль торцевой в большом сечении (инструментальный); m_ср – расчетный, по среднему сечению зуба.

В конической передаче основной расчетный параметр L.

; (3.1)

Передаточное отношение определяется:

. (3.2)

Основной критерий работоспособности конической передачи – контактная прочность.

Используется формула Герца:

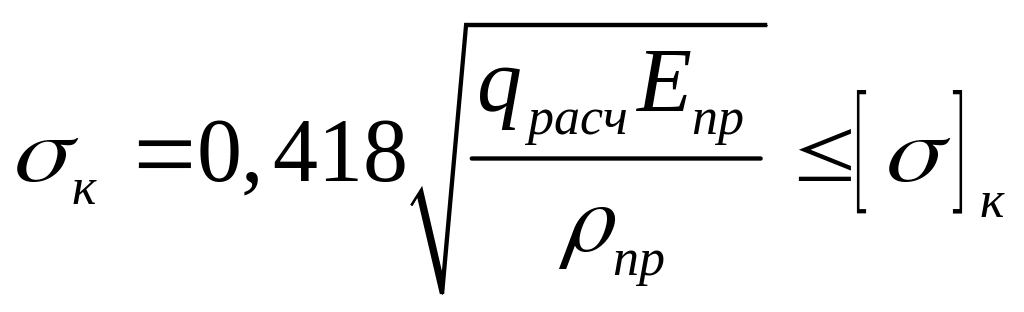, (3.4)

где q_расч – удельная расчётная нагрузка по ширине зуба с учётом коэффициентов k_конц и k_дин; E_пр – приведённый модуль упругости; ρ_пр – приведённый радиус кривизны.

, (3.5)

где q – удельная нагрузка по ширине зуба.

. (3.6)

Методика определения габаритов конической передачи

Окружная сила определяется:

, (3.7)

где М_ш и М_к – соответственно моменты на шестерне и колесе; D_ш и D_к – диаметры шестерни и колеса по среднему сечению.

Исходя из геометрии конической передачи (рис. 3.1):

; (3.8)

; (3.9)

; (3.10)

. (3.11)

_{Рис. 3.2. Схема сил, действующих в конической передаче}

_{Определяем удельную нагрузку q и qрасч по уравнению (3.5).}

; (3.12)

Приведённый радиус кривизны:

, (3.13)

где i – передаточное число (см. уравнение (3.2)).

Подставляем всё в формулу Герца:

. (3.14)

Получаем формулу для проверочного расчета конической зубчатой передачи по контактным напряжениям, где N_р – расчётная мощность на входном валу шестерни.

Формула для проектного расчета:

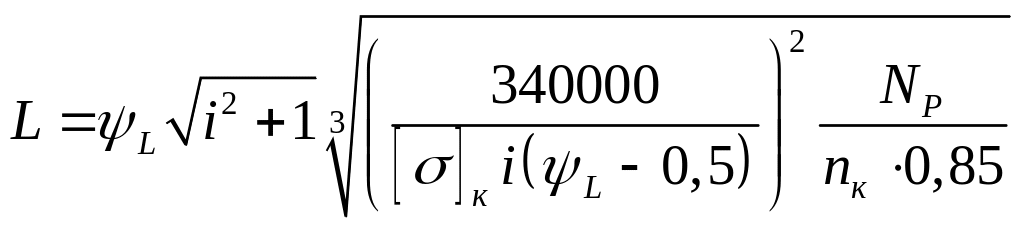. (3.15)