2 Профиль витка червяка .1.2. Определение усилий, действующих в червячной передаче

n-n

Рис. 2.3. Усилия, действующие в червячной передаче (1 – червяк, 2 – червячное колесо)

В червячной передачи действуют следующие силы:

P₂₁ⁿ – нормальная сила, которая направлена перпендикулярно к профилю червяка;

P₂₁^r– радиальная сила, действующая по радиусу червяка;

P₂₁^' – горизонтальная реакция нормальной силы;

P₂₁ – окружная сила на червяке;

P₁₂ – окружная сила на колесе;

P₂₁^а – осевая сила червяка (реакция колеса на червяк по оси).

За счет наличия скорости скольжения добавляется ρ*.

Таким образом в червячной передаче действуют 3 пары сил:

1. P₁₂ = P₂₁^а

2. P₂₁ = P₁₂^a

3. P₂₁^r = P₁₂^r

В соответствии с рис. 2.3 получаем формулы для определения сил в червячной передаче. Определяем удельную нагрузку q:

,

где L – длина контактной линии.

Основной расчётной силой является P₂₁ⁿ – сила действующая перпендикулярно к профилю зуба.

Порядок её определения:

;

;

;

;

;

;

Рис. 2.4. Профиль зуба венца червячного колеса

Для определения удельной нагрузки q необходимо знать длину контактной линии L:

,

где ε_s – коэффициент перекрытия (ε_s = 1,2 ÷ 1,3); b – ширина зуба червячного колеса; λ – коэффициент неполного прилегания зуба колеса к витку червяка (λ = 0,8).

.

В результате получаем выражение для удельной нагрузки:

;

,

где k_конц ≈ 1,35 ÷ 1,4 – коэффициент концентрации нагрузки в ножке зуба; k_дин ≈ 1,4 ÷ 1,5 – коэффициент динамической нагрузки.

Подставляем всё в формулу Герца:

,

где q – относительный диаметр червяка (см. табл. 2.1).

[σ]_к определяется в зависимости от материала и скорости скольжения (см. табл. 2.2).

Таблица 2.2

Допускаемые напряжения для червячных передач

Материал	[σ]к, кг/см2						[σ]из, кг/см2
	Скорость скольжения, м/с
	1	2	3	4	5	6
АЖ 9-4	2300	2100	1800	1600	1400	1200	800

Формула для проектного расчета червячной передачи:

.

2.1.3. Проверка габаритов червячной передачи по напряжениям изгиба

Проверка прочности ведется всегда по зубу колеса, так как венец зубчатого колеса изготовлен из менее прочного материала – бронзы АЖ 9-4.

σ_из < [σ]_из

,

где b – ширина колеса; m_n – модуль нормальный, m_n = m_s cosφ; y – коэффициент формы зуба (см. табл. 2.3); k_изн – коэффициент износа.

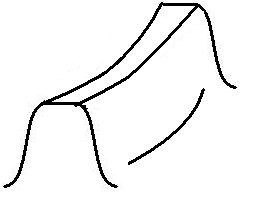
Рис. 2.5. Эвольвентный зуб колеса

Зуб колеса всегда эвольвентный и при износе теряет свою форму, в середине зуб колеса всегда тоньше чем по краям, поэтому его необходимо считать по напряжениям изгиба.

Таблица 2.3

Значение коэффициента формы зуба – y

z	20	24	26	28	30	32	35	37
y	1,98	1,88	1,85	1,8	1,76	1,71	1,64	1,61
z	40	45	50	60	80	100	150	300
y	1,55	1,48	1,45	1,4	1,34	1,3	1,27	1,24

В результате износа зуб теряет свою форму и σ_из может быть больше [σ]_из. Поэтому вводится коэффициент износа.

20% → k_изн. = 0.65.

[σ]_из – зависит от материала (см. табл. 2.2).