1.2. Определение габаритов планетарной и прямозубой передач им на примере схемы 7
Рис. 1.4. Одноступенчатая планетарная и прямозубая передача ИМ
Исходные данные:
схема
7
Ду
= 150 мм
Р
= 10 кг/см2
V
= 5 мм/с
Nдв
= 1 кВт
nдв
= 750 об/мин
dшп
→ (см. приложение
I
– d17)
мм
d17
= 24×2×5, где
24 – наружный диаметр
резьбы, мм
2 – заходность резьбы
(
5
– шаг резьбы (
,
мм
По исходным данным определяем:
об/мин, Nдв
и nдв.
см. часть 1 раздел 3.5.
1.2.1. Расчет планетарной части им
а)Кинематический расчёт.
Определяем общее передаточное отношение всего ИМ:
.
Принимаем передаточное
отношение одноступенчатого планетарного
редуктора
=
5,5 (см. часть
1 табл. 3.3).
Определяем числа зубьев у колес планетарной передачи. Выбираем za = 21 (число зубьев za должно делиться на 3, чтобы нагрузка распределялась равномерно).
Определяем число зубьев неподвижного колеса:
– делится на 3.
Соблюдается условие соостности
,
поэтому .zb = 96.
Число оборотов саттелита:
.
Исходя из условия соседства:
;
;
50,6 > 40.
Действительное передаточное отношение:
,
незначительно отличается от заданного – 5,5
Число оборотов водила:
;
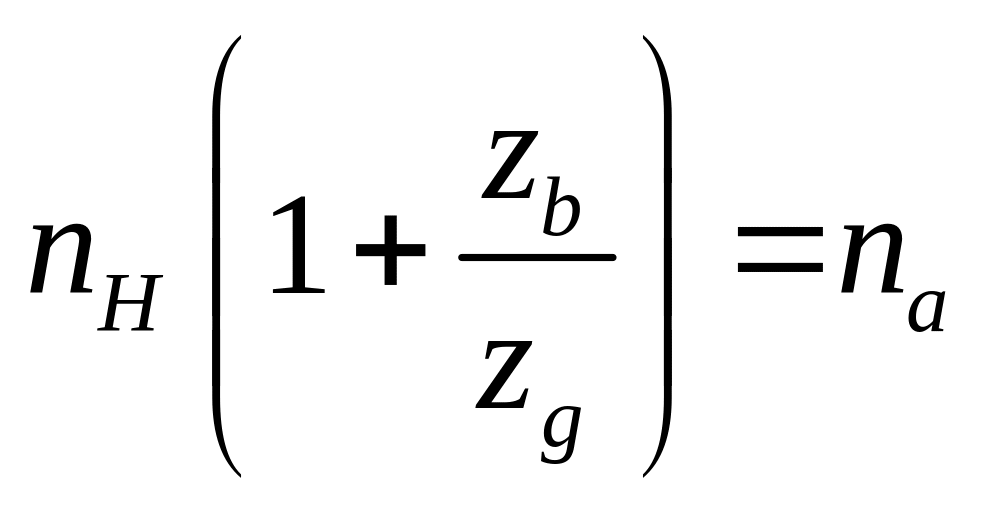об/мин.
Ранее определили nвых.ред = 30 об/мин.
Передаточное отношение прямозубой передачи:
.
; 
Принимаем nH = n1 = 135, где n1 – число оборотов малой шестерни прямозубой передачи.
б) Определение габаритов планетарной передачи.
Определяем размеры колес пары a – q.
Выбираем прямозубое, некоррегированное зацепление, назначаем материал колеса а cm 40X. Тогда для колеса a твердость HB280 (т.к. оно чаще бывает в зацеплении), для q – сателлита HB250.
По рекомендациям допустимое контактное напряжение определяется как:
кг/см2.
Определяем расчетную мощность:
кВт,
где Kр = 1,3.
Для определения диаметра dа по формуле исходя из контактных напряжений принимаем следующее соотношение ширины колеса и его диаметра.
,
т.е. ширина шестерни – это половина диаметра, b = 0.5 · dа.
Компенсирующее устройство для оси da отсутствует, поэтому коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами, принимаем KH = 1,2.
Для рассматриваемой пары a – q:
.
Число оборотов колеса q – сателлита:
об/мин.
Подставляем эти значения в формулу для расчета по контактным напряжениям:
;
мм.
Определяем модуль планетарной передачи:
мм.
Принимаем m = 1,5 мм из нормального ряда.
Тогда:
da = m za = 1,5 · 21 = 31,5 мм – центральное колесо,
dg = m zg = 1,5 · 38 = 57 мм – сателлит,
db = m zb = 1,5 · 96 = 144 мм – неподвижное колесо.
в) Проверяем модуль по напряжениям изгиба.
Зубья планетарной части редуктора, также как и прямозубой работают двумя сторонами (задвижка открывается, задвижка закрывается).
Необходимо проверить неравенство
σиз < [σ]из .
Допустимое напряжение:
,
где
– предел выносливости при знакопеременном
цикле напряжений; 
– коэффициент запаса прочности – 1.5;
Kσ
– коэффициент концентрации напряжений
у ножки зуба – 1.8.
По рекомендациям
.
σвр для ст40X – 7000кг/см2,
кг/см2.
кг/см2.
Для определения действительного изгибного напряжения необходимо знать окружное расчетное усилие, действующее на зуб колеса:
,
где 
– расчетный момент на малой шестерне.
кг/см2.
Из предыдущих расчетов диаметр центральной шестерни da = 31,5 мм.
кг/см2;
кг/см2,
где b – ширина зуба наиболее нагруженной центральной шестерни – da.
мм.
y = 0,376 – коэффициент формы зуба, определяемый по табл. 2.3.
Принимаем b = 16 мм.
В результате действительное напряжение, возникающее в зубе, меньше допустимого:
465 < 1166 кг/см2.
Условие прочности зуба на изгиб соблюдается.