Часть 2

Определение габаритных размеров исполнительных механизмов систем управления

1. Расчёт планетарных и прямозубых передач ИМ

(на примере схемы 7)

1.1. Теоретическая часть

Быстроходная часть ИМ – планетарная передача

Прямозубая передача

одноступенчатая планетарная передача

Вход, двигатель

g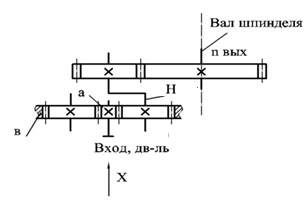

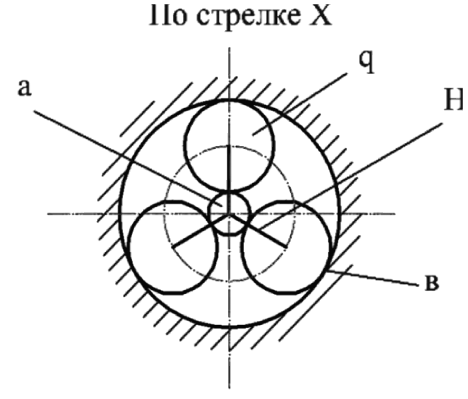
Рис. 1.1. Одноступенчатая планетарная и прямозубая передачи (схема 7)

Планетарными называют передачи, включающие в себя зубчатые колеса с подвижными осями (рис. 1.1).

Одноступенчатая передача состоит из центрального колеса a с наружным зацеплением, центрального колеса в с внутренним зацеплением (неподвижного) и водила Н, на котором укрепляются оси сателлитов g.

Сателлиты вращаются вокруг своих осей и вместе с осью вокруг центрального колеса а, т.е. совершают движение, подобное движению планет. Отсюда название – планетарные передачи.

При неподвижном колесе в движение передается от а к Н.

Достоинством планетарной передачи является компактность и малый вес, что очень важно для исполнительных механизмов систем управления. Мощность передаётся по нескольким потокам, число которых равно числу сателлитов (в нашем случае распределяется на три потока). При этом нагрузка на зубья в каждом зацеплении уменьшается в 3 раза.

Планетарный принцип позволяет получить большие передаточные отношения без применения многоступенчатых передач, уменьшенную нагрузку на опоры, так как при симметричном расположении сателлитов силы в передаче взаимно уравновешиваются.

Недостаток планетарных передач: повышенные требования к точности изготовления и монтажа.

а). Кинематические расчёты

При исследовании кинематики планетарных передач используется метод остановки водила – метод Виллиса.

Всей планетарной передаче мысленно сообщается вращение с числом оборотов водила, но в обратном направлении. Получаем механизм, представляющий собой простую передачу, в которой движение передается от а к в через паразитное колесо g (колесо в не закреплено).

Числа оборотов зубчатых колес приведённого механизма равны разности чисел оборотов и числа оборотов водила.

Передаточное отношение для приведенного механизма будет равно:

, (1.1)

где n_a – число оборотов колеса а; n_b – число оборотов колеса в; n_H – число оборотов водила Н.

Сателлит является в данном случае паразитным колесом, т.к. не участвует в образовании передаточного числа.

Обозначение расшифровывается таким образом: направление движения от колеса а к колесу в, Н – неподвижное звено (в данном случае – водило).

В планетарных передачах существенное значение имеет знак передаточного отношения.

Если i > 0, то вращение ведущего и ведомого звеньев в одном направлении. Если i < 0 – вращение колёс противоположное.

В рассматриваемом примере колеса а и в вращаются в разных направлениях, поэтому < 0.

В реальном механизме колесо в закреплено, а – колесо ведущее, H – ведомое (водило).

При n_b = 0:

.

Разделим на n_H:

.

Тогда:

(1.2)

б) Силы в зацеплении.

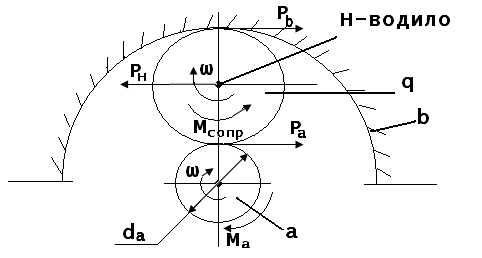
Рис. 1.2. Силы в зацеплении планетарной передачи

Из условия равновесия сателлита а:

P_a = P_b,

P_H = -2P_a,

, (1.3)

где c – число сателлитов; K_H – коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами (К_Н =1,2 ÷ 1,8).

в) Расчет на прочность

Расчет на прочность зубьев планетарной передачи ведется так же, как для простой зубчатой передачи: для наружного зацепления а – g, для внутреннего g – в. Силы и модули в этих зацеплениях одинаковы, внутреннее зацепление по своим свойствам прочнее наружного, поэтому при одинаковых материалах достаточно рассчитать зацепление а – g. Наружные габариты планетарных передач определяются диаметром наружного колеса в.

Расчет планетарной передачи по контактным напряжениям ведется по формуле:

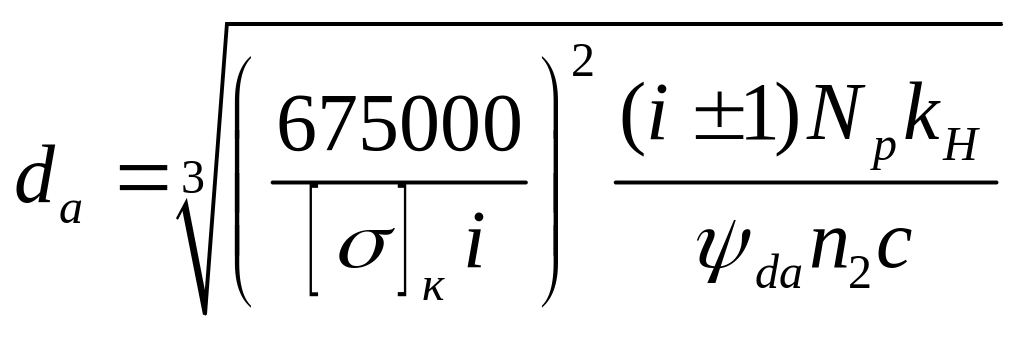, (1.4)

где Nр – расчётная мощность на валу d_a; i – передаточное число, определяемое как отношение большего числа зубьев рассчитываемой пары к меньшему; d_a – диаметр меньшего колеса из пары, n₂ – число оборотов большего из пары; ψ_da – коэффициент ширины зуба по диаметру (0,6 ÷ 0,75); c – число сателлитов; k_H – коэффициент неравномерности распределения нагрузки по ширине зуба (1,5 ÷ 1,6).

г) Определение числа оборотов сателлита.

Рассмотрим одноступенчатую планетарную передачу при остановленном водиле и известном n_а:

,

где числа оборотов n_g и n_a обратно пропорциональны числам зубьев.

Расчетная мощность Nр определяется при выборе электродвигателя (см. часть 1 п. 3.5).

д) Выбор числа зубьев.

Выбор числа зубьев сателлита предшествует расчету на прочность. При заданном число зубьев определяется по уже рассмотренной формуле. Полученные значения числа зубьев колёс уточняются по 3-м условиям собираемости планетарной передачи.

1. Условие соосности:

,

или

.

2. Условие симметричного размещения сателлитов.

Требуется, чтобы z_a и z_b были кратны числу сателлитов с .

– должно быть целое число.

3. Условие соседства предусматривает наличие гарантированного зазора между сателлитами.

или

, (1.5)

где m – модуль сателлита.

е) Особенности кинематического расчета двухступенчатой планетарной передачи

двухступенчатая планетарная передача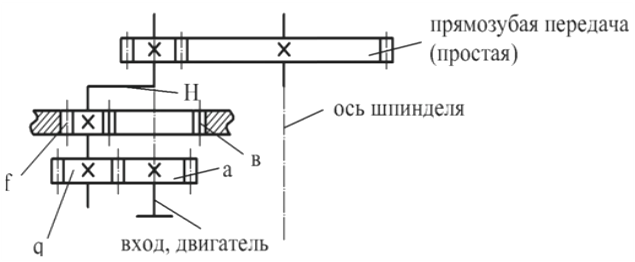

Рис. 1.3. Двухступенчатая планетарная и прямозубая передачи

Передаточное отношение при движении от центрального колеса а к водилу Н в двухступенчатой планетарной передаче:

. (1.6)

Передаточное отношение двухступенчатой планетарной передачи увеличивается по сравнению с одноступенчатой передачей.