4.3. Коэффициент теплопередачи

Во многих случаях при использовании тонкостенных труб для определения коэффициента теплопередачи сложного теплообмена используют упрощенную формулу для плоской пластины [2;3]:

.

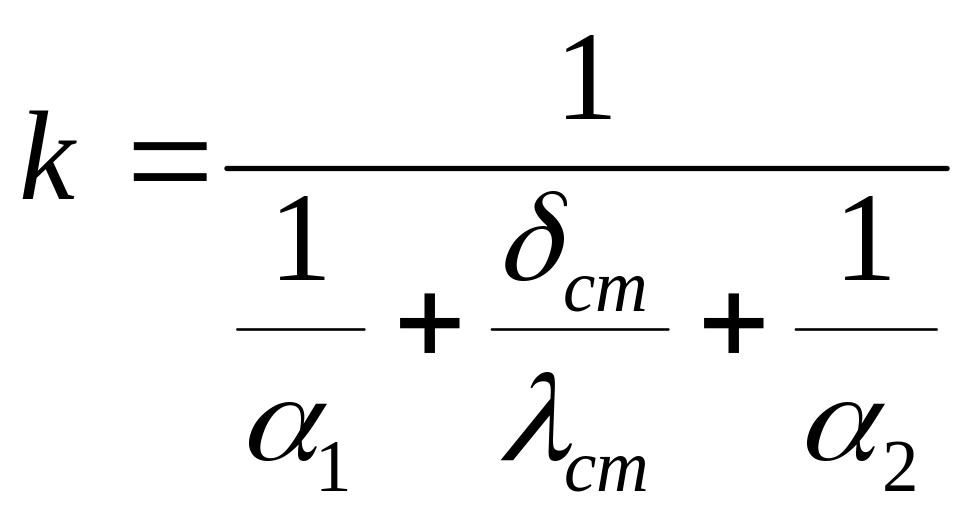Пример. Определить тепловую мощность батареи отопления из задачи 7, состоящую из 10 труб (5 регистров).

Решение. Используем для решения задачи известное соотношение между мощностью и коэффициентом теплопередачи

Q=k∙S_то∙t_л,

где k – коэффициент теплопередачи, определенный в предыдущей задаче на уровне k=20 Вт/(м²∙К); t_л – температурный напор между поверхностью нагрева и окружающим воздухом, в рассматриваемом случае он постоянный и имеет значение t_л=t_нагр-t_окр=70ºС; S_то – поверхность теплообмена:

S_то= πd∙H∙n.

Таким образом, мощность батареи равна

Q= πd∙H∙n∙k∙t_л=3,14∙0,05∙1∙10∙20∙70=2198 Вт.

Задача 9. Определить коэффициент теплопередачи в конденсаторе турбины при α_ох = 1000 Вт/( м²∙К), α_гр = 5000 Вт/( м²∙К), если трубчатка выполнена из сплава МНЖ-5-1 Ø25х1.

Задача 10. Определить мощность теплообменника, трубчатка которого состоит из трубок Ø 20х1,5 из стали 20 длиной 3м, коэффициент теплоотдачи в трубах α_ох=3000 Вт/(м²∙К), температура на входе 20ºС, на выходе 40ºС; греющая среда – пар с Рs=2,0 МПа, α_гр = 4000 Вт/(м²∙К).

Задача 11. Определить коэффициент теплопередачи и обосновать целесообразность использования интенсификаторов теплообмена в следующих случаях:

- в нержавеющей трубке Ø25х2,5 из стали ОТХ18Н10Т движется вода, обеспечивая α_гр=2000 Вт/(м²∙К); а снаружи она омывается воздухом с α_ох=10 Вт/(м² ∙К);

- в трубке из стали 20 Ø20х1 соответственно α_гр=2000 Вт/(м² ∙К) и α_ох=1000 Вт/(м² ∙К)

- в латунной трубке (Ло-90) Ø19х1,5 протекает вода α_ох=5000 Вт/(м²∙К), а снаружи конденсируется пар с α_гр=4000 Вт/(м² ∙К).

5. Оптимизация конструкции трубчатки

Иногда при проектировании теплообменного оборудования уровень расходов греющей или обогреваемой среды может быть настолько мал, что возникают проблемы в организации турбулентного режима течения в теплообменных трубках или межтрубном пространстве. Эта проблема может быть решена путем многоходового течения сред через меньшее количество труб или меньшие проходные сечения.

Критерий целесообразности многоходовой компоновки теплообменного оборудования, как правило, заключается в том, что используемые в тепловых расчетах критерии подобия применимы только для турбулентных режимов течения. Этот режим ограничивается значениями чисел Рейнольдса R_е  10⁴. Следовательно, при определенной конструкции аппарата и установленных из баланса тепла расходах должна иметь место минимальная скорость потока через проходное сечение трубного и межтрубного пространства.

Количество ходов определяется путем решения неравенств.

где  скорость среды, м/с.

В случае протекания среды в трубах: .

Эквивалентный диаметр определяем по формуле: , а решение неравенства в этом случае будет иметь вид .

В случае протекания среды в межтрубном пространстве эквивалентный диаметр

,

где S_пр проходное сечение м²,

;

П =    D + d_тр  n   смоченный периметр, м;

D – диаметр корпуса или кожуха, в котором размещена трубчатка, м.

В этом случае максимальное количество труб n или диаметр корпуса аппарата D, при котором режим течения сохраняется турбулентным, определяются из неравенства

.

Поверхность теплообмена обосновывается тепловой мощностью, существующими температурными напорами и коэффициентом теплопередачи К и определяется из следующего выражения:

.

Геометрически поверхность теплообмена определяется диаметром труб, длиной и их количеством n:

S_ТО =   d   n .

При заданном типоразмере теплообменных трубок из ряда: 10, 12, 14, 16, 18, 19*, 20, 24, 25, 28, 30, 32 (* - используются обычно латунные трубы).

Таким образом, теплообменная поверхность может варьироваться значениями и n.

В результате расчетов по приведенным формулам в некоторых случаях может принимать недопустимые очень большие размеры.

В этом случае длинные теплообменники разделяют на короткие многоходовые.

Пример. Определить наименьшее количество трубок n_тр для организации турбулентного режима течения, если известно, что объемный расход через трубки Ø20х1 составляет 0,2 · 10ˉ ³м³/с при температуре 100 ºС и давлении 100 кПа.

Решение. Турбулентный режим течения определяется значением критерия Рейнольдса неравенством

,

где кинематическая вязкость рассчитывается для данных условий по значениям динамической вязкости  и удельного объема V, которые в свою очередь, определяются по таблицам [4]:

=∙=300∙10^-6∙0,001043=0,3∙10^-6;

=300 мкПа∙с; =0,01043 м³/кг.

Решение этого неравенства представлено выше:

шт.

Для соблюдения неравенства округляем в меньшую сторону, т.е. выбираем 4 трубки.

Задача 12. Определить наименьшее количество параллельно включенных трубок Ø12х1 для организации турбулентного режима течения при общем расходе через них 4· 10^-3 м³/с при температуре 20ºС и давлении 200 кПа.

Задача 13. Определить наименьшее количество трубок n_тр, их длину и количество ходов n_х в прямотрубном противоточном теплообменном аппарате Q=100 кВт, k=500 Вт/(м²∙К), имеющего следующие параметры сред:

- в трубчатке ø18Х1,5 вода Р_тр=1,6 МПа; G_тр=10кг/с t^’=150ºC;

- в межтрубном пространстве Р=0,5 МПа; t`_м=20C; t``_м=90 C.

Задача 14. Разработать конструктивные предложения по межтрубному пространству теплообменника для организации турбулентного режима течения в корпусе диаметром 100 мм, в котором размещено 10 трубок  12х1. Объемный расход воды с температурой 20 C и давлением 200 кПа составляет 1,0·10^-3 м³/с.