3.4.2. Интегрирование простейших иррациональных функций
Рассмотрим интегралы вида
(3.4.9)
где
подынтегральная функция рациональна
относительно переменной интегрирования
х
и различных радикалов из х.
Пусть n
– наименьшее кратное показателей r,
m,…,
тогда все отношения
– целые числа. Интеграл (3.4.9) приводится
к интегралу от рациональной функции
заменой переменной
Действительно,
интеграл (3.4.9) примет вид
и подынтегральное выражение есть
рациональная функция от z.
Пример
4. Вычислить
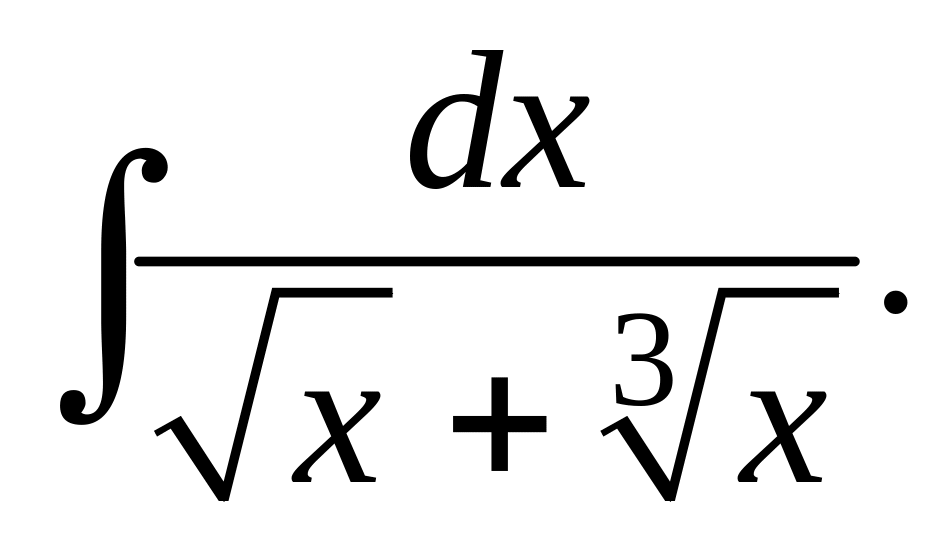
Наименьшее
кратное чисел 2 и 3 есть – 6. Положим
тогда
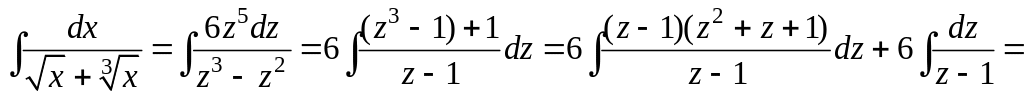
где
(из х
= z6).
Схема интегрирования останется прежней и в более общем интеграле
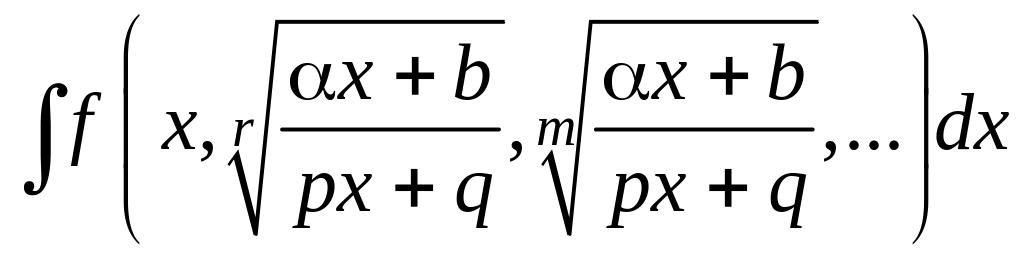(в
частности может быть px
+ q
= 1).
Интеграл
рационализируется заменой
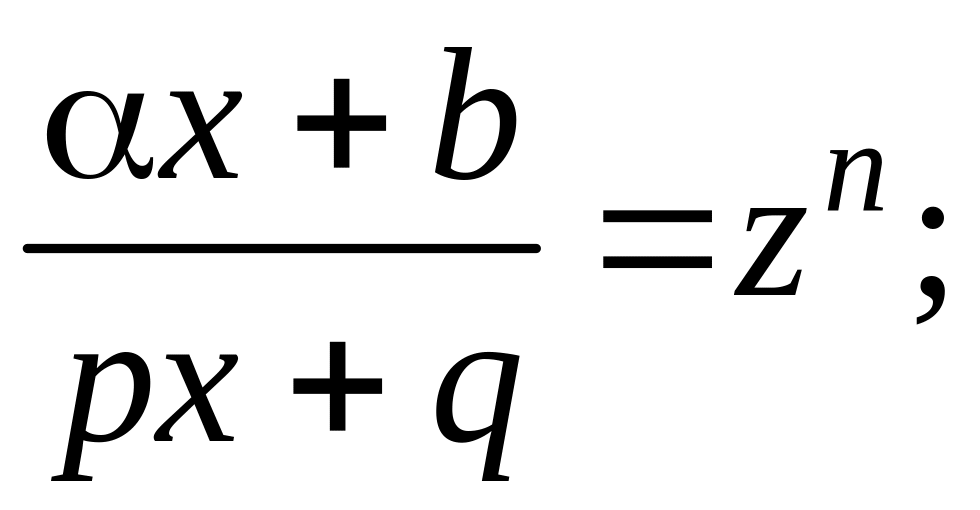
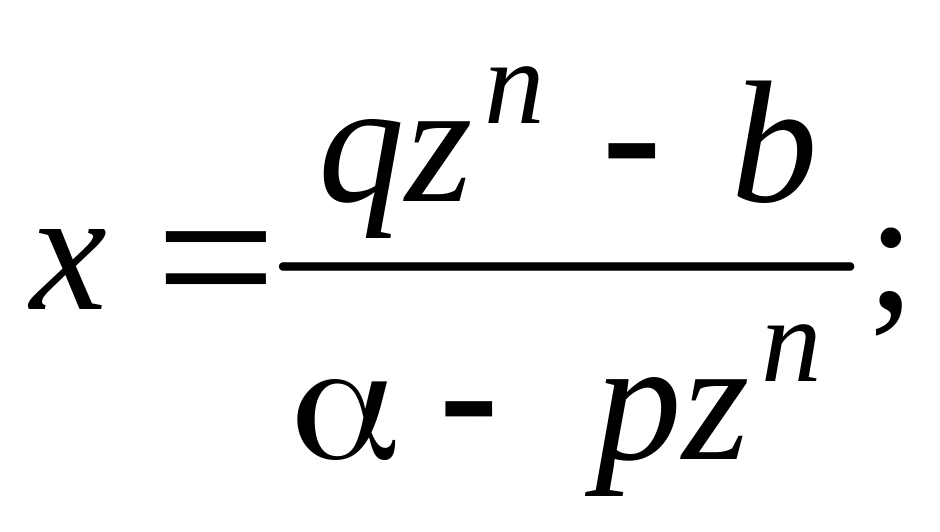
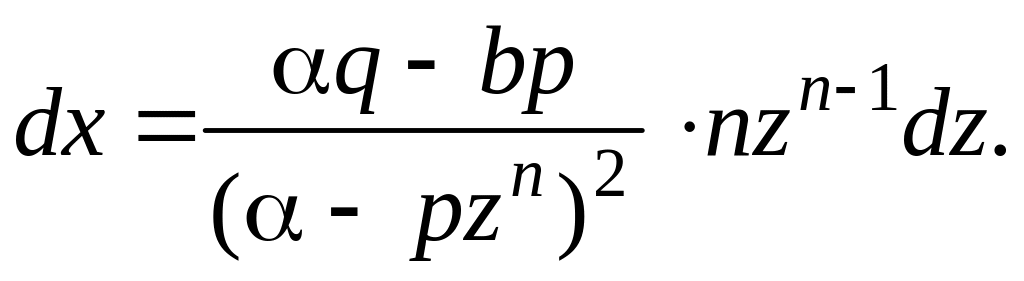
Пример
5.
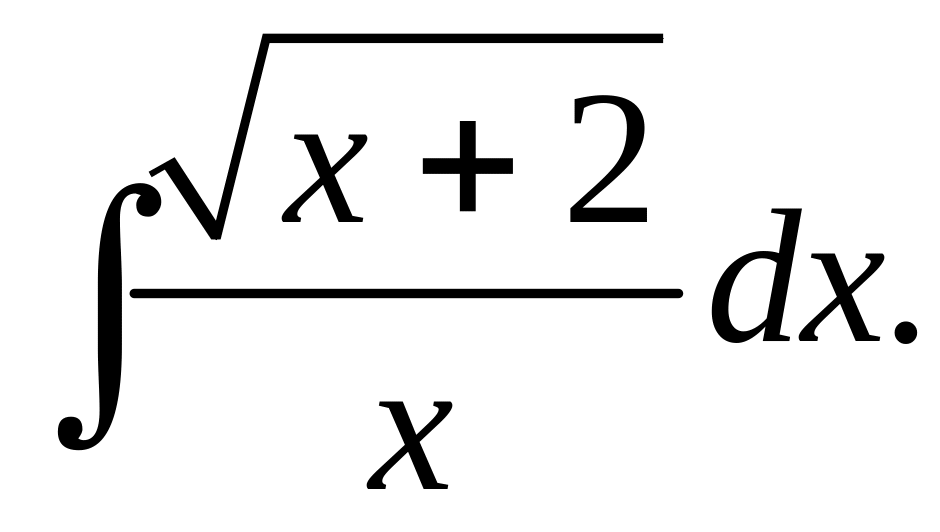Положим
тогда
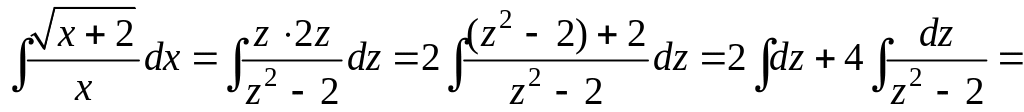
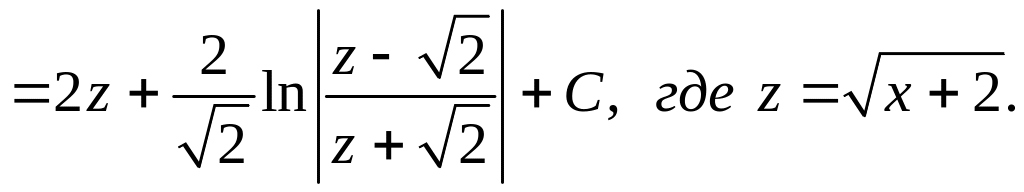
Интеграл
вида
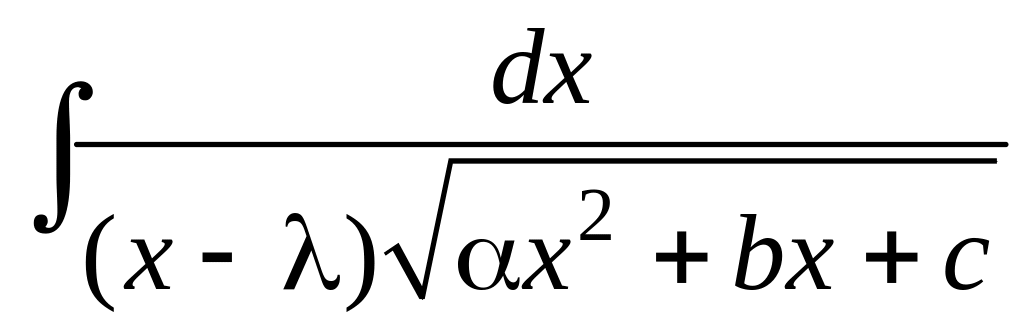заменой
сводится к интегралу, содержащему
квадратный трехчлен. В частном случае
(λ = 0) применяют подстановку
.
Пример
6. Найти
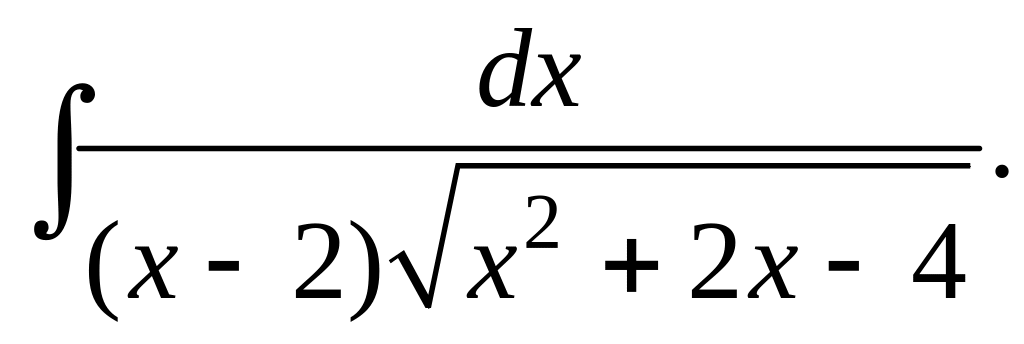
Положим
в результате получим
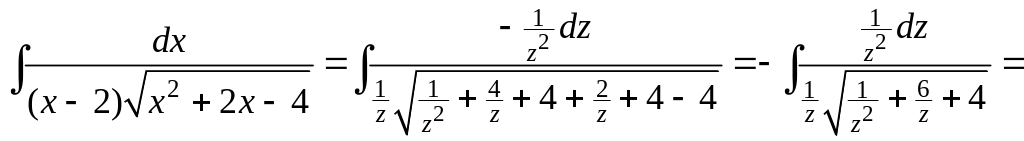
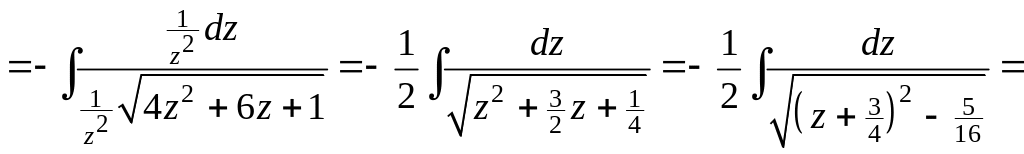
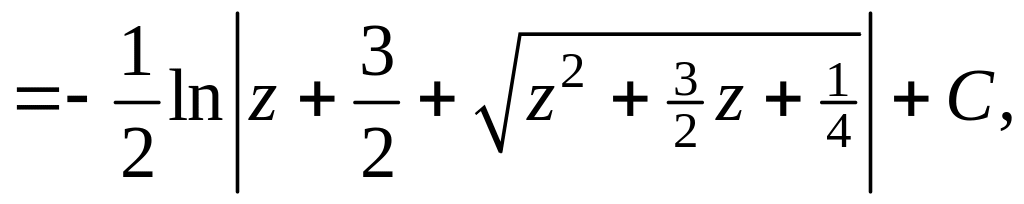где
Вывод. В настоящей лекции рассмотрены методы нахождения первообразных от рациональных функций, которые часто встречаются в прикладных задачах, а также интегрирование простейших иррациональностей. Это должно способствовать дальнейшему формированию компетенции – применять простейшие методы интегрирования.
Лекция 3.5. Интегрирование тригонометрических функций
Любую тригонометрическую функцию можно свести к функции от sinx или cosx.
Рассмотрим
интеграл вида
(3.5.1)
Существует достаточно много подстановок, сводящих его к интегралу от рациональной функции.
Правило 1.
1. Если при замене sinx на –sinx R(sinx,cosx) меняет свой знак на противоположный, то нужно сделать замену z = cosx.
2. Если при замене cosx на –cosx R(sinx, cosx) меняет свой знак, то нужно сделать подстановку z = sinx.
3. Если при замене sinx на –sinx, cosx на –cosx R(sinx,cosx) не меняет своего знака, то нужно сделать замену z = tg x.
Пример
1. Вычислить
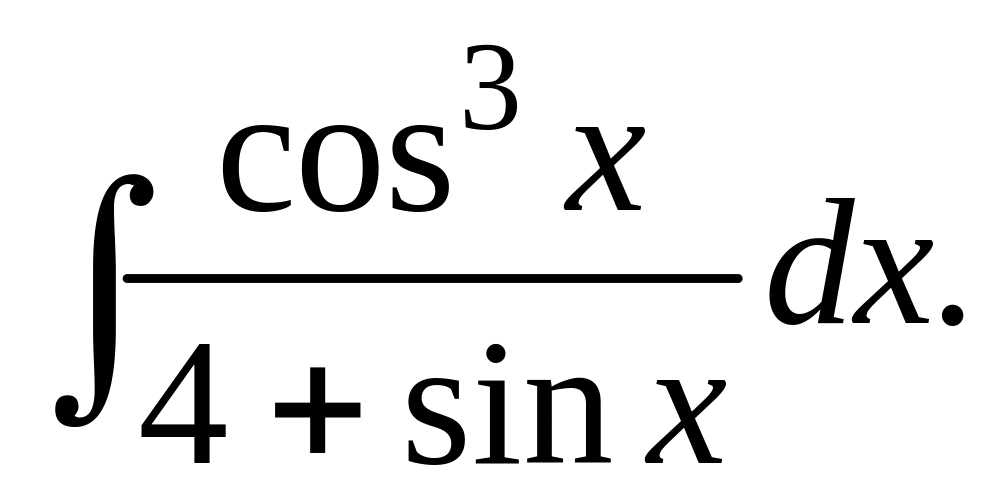Ясно, что при замене cosx
на –cosx
подынтегральное выражение изменит свой
знак. Делаем подстановку z
= sinx;
dz
= cosxdx.
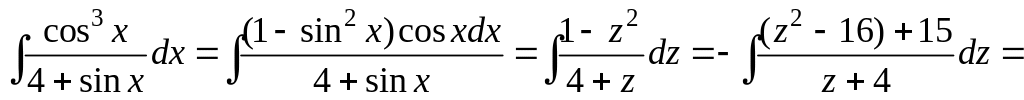
Пример
2.
Применяем третий пункт правила 1.
Подстановка z
= tg
x;
x
= arctg
z;
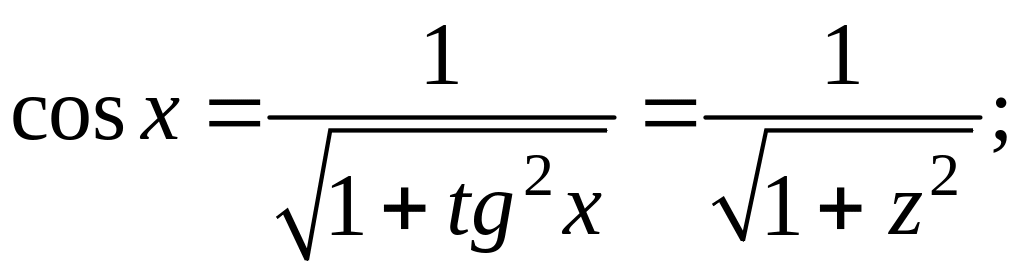
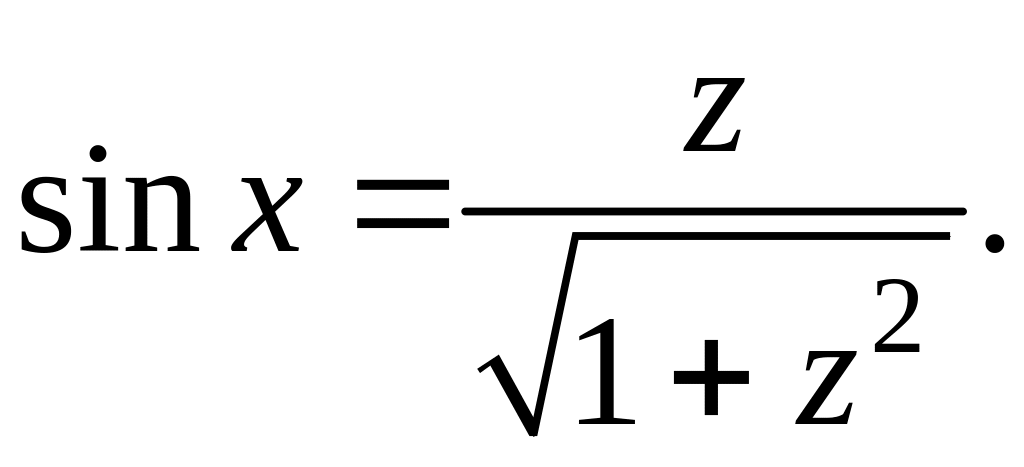
Отсюда
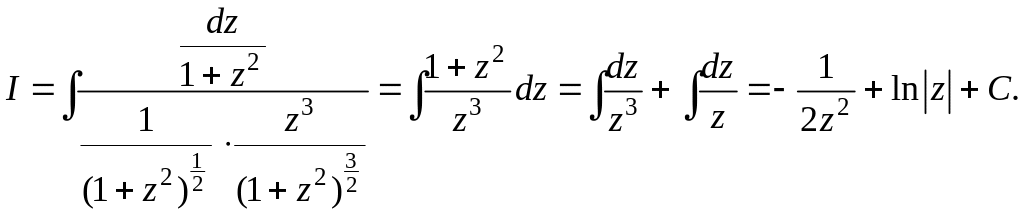
В
итоге
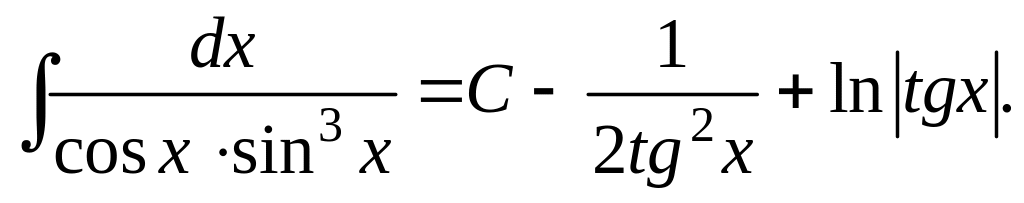
3.5.1. Универсальная подстановка
Интеграл
(3.5.1) подстановкой
всегда преобразуется в интеграл от
рациональной функции.
Из
равенства х = 2arctgx
находим
.
По тригонометрическим формулам
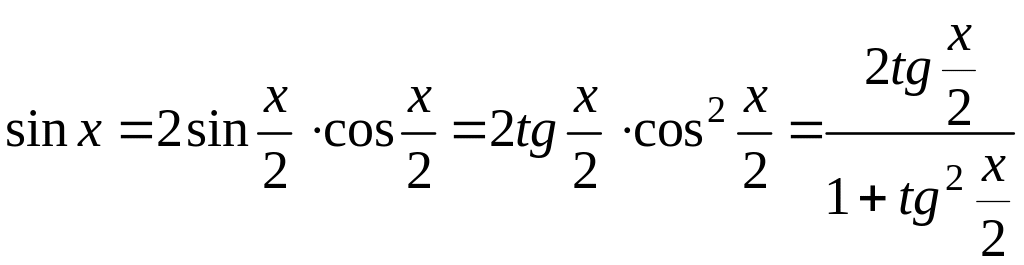
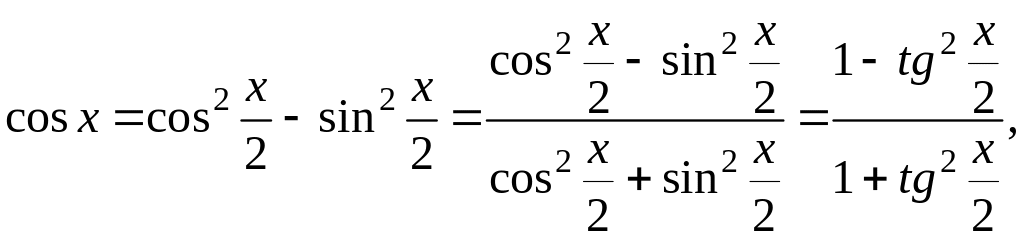т.е.
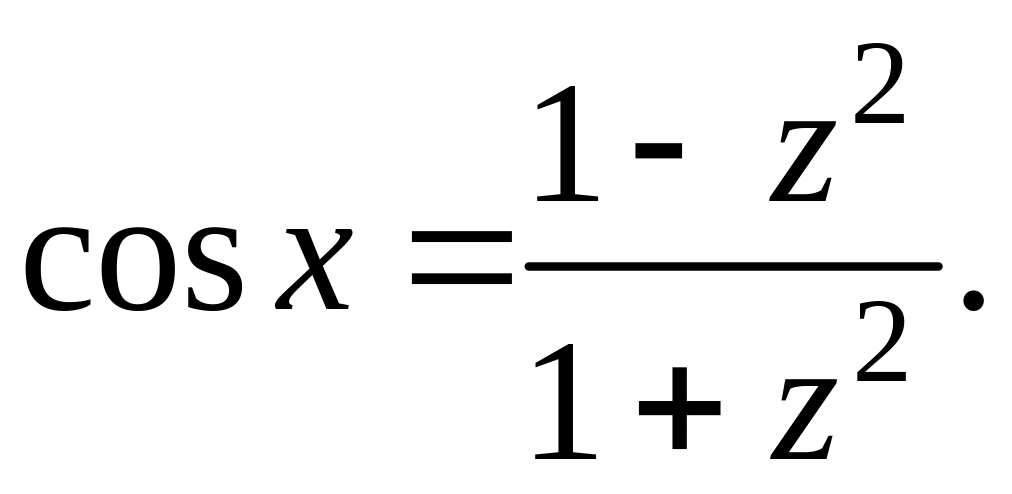
Итак
,
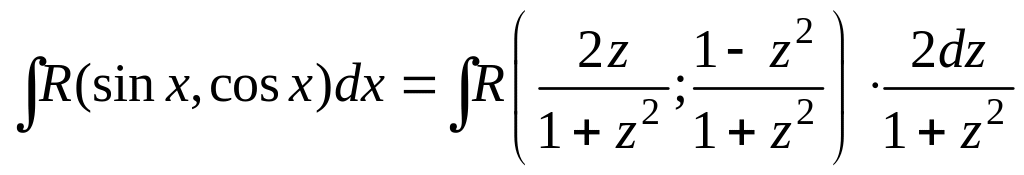т.е. подынтегральная функция становится
рациональной относительно z.
В силу своей общности подстановка
очень часто является не наилучшей в
смысле краткости и простоты необходимых
преобразований. С помощью универсальной
подстановки очень удобно вычислять
интегралы вида
(3.5.2)
Пример
3. Найти
Интеграл
типа (3.5.2) – поэтому подстановка
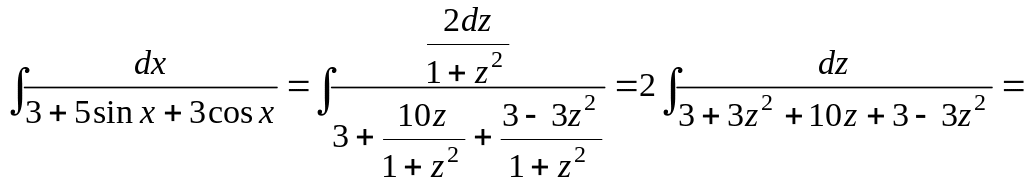
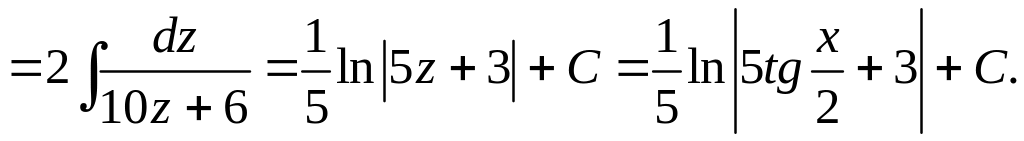
Универсальную подстановку обычно применяют в тех случаях, когда sinx и cosx входят в рациональную функцию в нечетной степени. Если в выражении функции R только четные степени sinx и cosx, то гораздо быстрее ведет к цели замена tgx = z, содержащая квадратные корни. Последние исчезают при выражении sinx и cosx через z.
Пример
4. Вычислить
интеграл
Замена
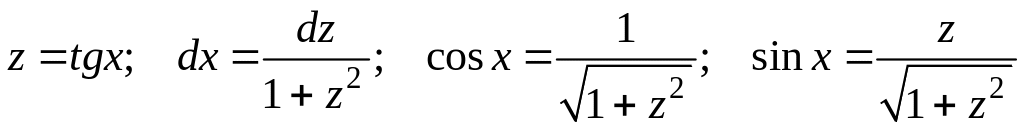дает
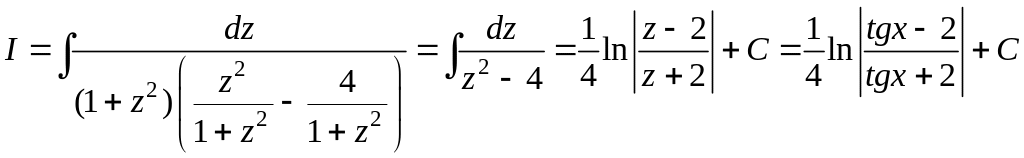
Не
трудно заметить, что применение
универсальной подстановки
привело бы к более длинным выкладкам.
В
интегралах вида
(3.5.3)
рассматривают несколько случаев:
1. Если m = 2r; n = 2k, т.е. обе степени четные и положительные числа (0-четное число), то при вычислении интеграла (3.5.3) применяют метод понижения степени по формулам удвоения углов:
Пример
5. Вычислить
интеграл
Перепишем
его в виде
и применим формулы удвоения углов, тогда
В первом интеграле правой части последнего равенства еще раз понизим степень, во втором сделаем замену 2cos2xdx = d(sin2x), в результате получим
2. Если m и n четные, но хотя бы один из показателей отрицательный, применяют подстановку z = tgx.
Пример
6.
Здесь m
= 0; n
= – 4.
В
результате замены: z
= tgx;
x
= arctgz;
имеем
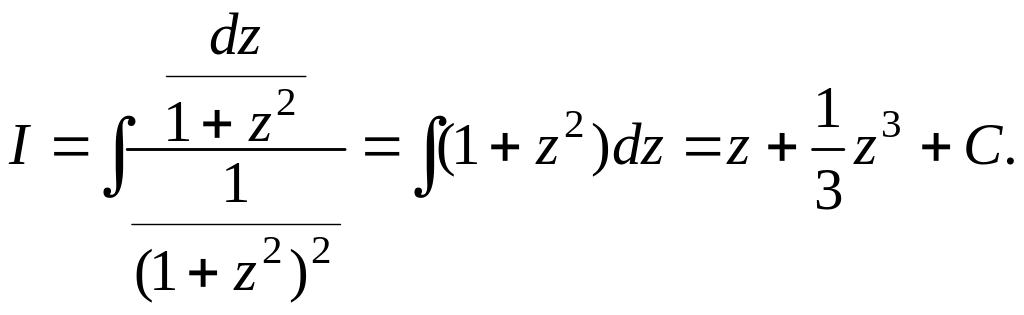
В
итоге
3. Когда степени m и n нечетные и положительные, пользуются заменой: z = cosx или z = sinx в зависимости от множителя, степень которого больше.
Пример
7. Найти
Степень sinx
больше, поэтому:
z = sinx; dz = cosxdx.
Интегралы
и
находят следующим приемом. Заменяют
на
на
и разбивают на сумму двух интегралов,
из которых первый легко берется, а у
второго степень становится на две
единицы меньше.
Пример
8. Вычислить
Применяя приведенное правило получим
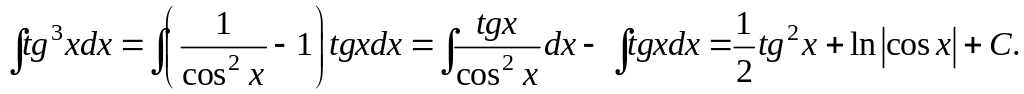
Пример
9. Найти
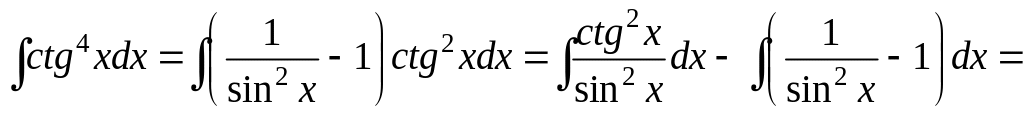
Рассмотрим в заключение интегралы:
1.
2.
3.
Они вычисляются путем замены произведений тригонометрических функций их суммой или разностью по формулам:
1.
2.
3.
.
В результате интегралы разбиваются на два табличных
Пример
10. Вычислить
Здесь m = 5, n = 2. По формуле 2 получим
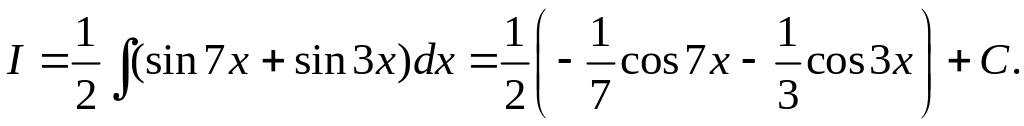
Пример 11.
В обоих случаях интегралы свелись к табличным.