3.3.2. Интегрирование по частям

Метод интегрирования по частям следует из дифференцирования произведения двух функций. Известно, что

откуда

Интегрируя обе части последнего равенства, получим:

или

(3.3.1)

Выражение (3.3.1) является формулой интегрирования по частям.

Данный метод состоит в том, что подынтегральное выражение f(x)·dx представляется каким-либо образом в виде произведения двух множителей u и dυ. Множитель u, стоящий в левом интеграле, при переходе к правому интегралу заменяется на du, т.е. дифференцируется. Другой сомножитель dυ из левого интеграла заменяется на υ, т.е. интегрируется. Надо так подынтегральное выражение представить в виде произведения двух сомножителей, чтобы обе операции составили в совокупности задачу более простую, чем непосредственное вычисление интеграла На практике чаще упрощение обусловлено дифференцированием множителя u.

Если в составе подынтегрального выражения имеется множитель, упрощающийся от дифференцирования, то его следует взять за «u», а все остальное (включая dx!) за «dυ».

Пример 7. Вычислить Ясно, что за «u» надо взять множитель х, так как при дифференцировании он «исчезает»

u = x, du = dx, и

Чтобы найти сделаем замену z = sinx; dz = cosxdx, тогда

Когда применяют интегрирование по частям и по dυ находят υ, то произвольной постоянной не вводят, присоединяя ее к произвольной постоянной второго, незавершенного интегрирования в правой части равенства (3.3.1).

Применяя формулу (3.3.1), получим:

Пример 8. Вычислить Здесь за «u» следует взять arctgx, тогда dυ =dx. Составим таблицу:

u = arctgx
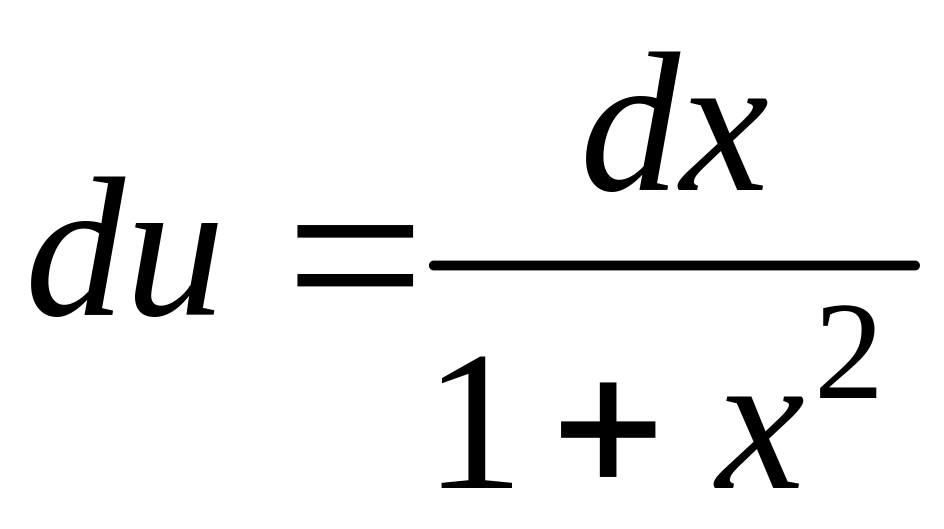
dυ =dx

применяя формулу интегрирования по частям (3.3.1) получим:

Пример 9. Вычислить интеграл За «u» принимаем х, тогда

u = х	du = dx

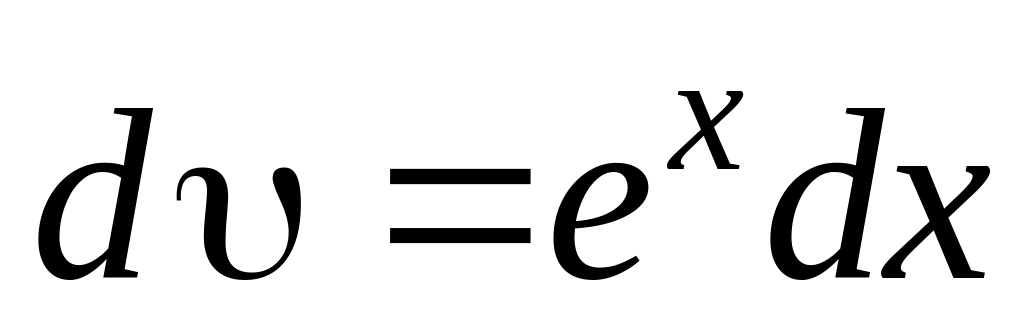
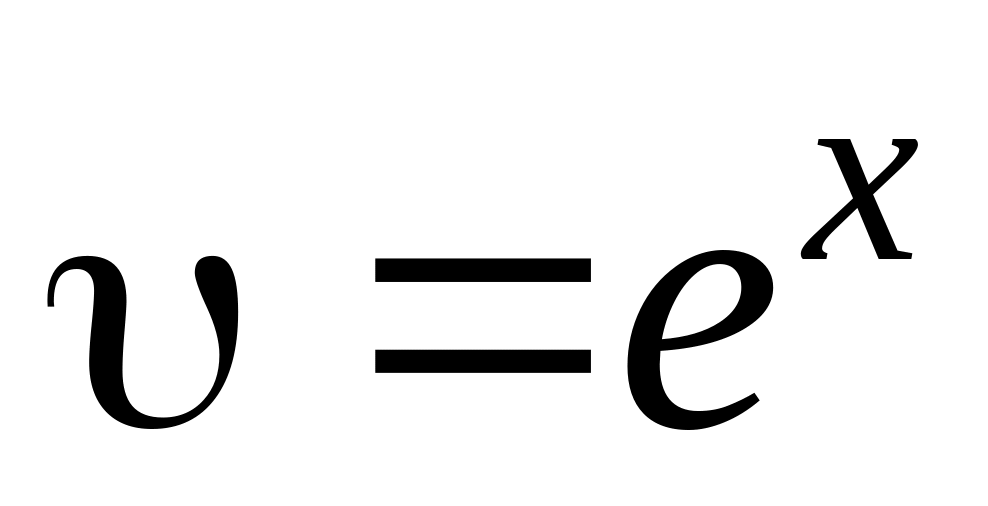
Применяя формулу (3.3.1) получим

Иногда интегрирование по частям приходиться применять несколько раз.

Пример 10. Вычислить

Разобьем подынтегральное выражение на части

u = х2	du = 2xdx
dυ = cosxdx	υ = sinx

Тогда

В последнем равенстве интеграл – проще исходного (то, что cosx заменился на sinx не изменяет сути решения, а вместо х² появился более простой множитель х).

К интегралу I₁ – снова применим интегрирование по частям, полагая

u = х	du = dx
dυ = sinxdx

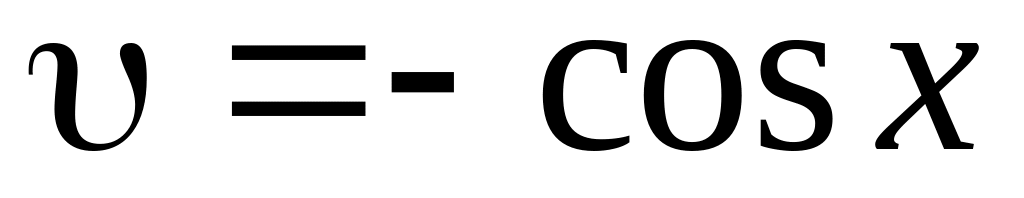
Это дает

Заменяя I₁ найденным выражением, окончательно получим

Практика показывает, что многократным интегрированием по частям можно найти интегралы следующих двух групп.

К первой группе относятся интегралы:

1. 2. 3. 4.

где Р(х) – многочлен некоторой степени, который и берется за функцию u. При многократном дифференцировании он «исчезает».

Ко второй группе относятся следующие интегралы:

1. 2. 3. 4.

Здесь нужно избавится от трансцендентных функций arcsinx, arccosx, arctgx и lnx, поэтому они принимаются за «u».

Пример 11. Вычислить Так как интеграл из первой группы, то

u = 2х + 3	du = 2dx

Применяя формулу интегрирования по частям, получим:

Пример 12. Найти Интеграл второй группы, следовательно

По формуле (3.3.1) находим

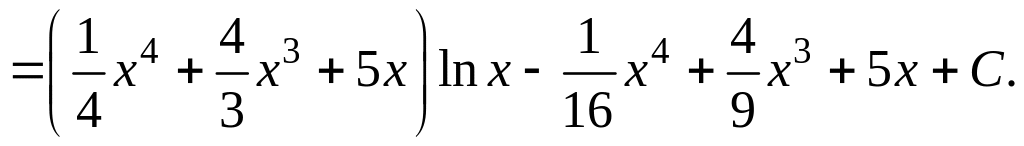
Повторное интегрирование по частям иногда приводит к первоначальному интегралу, и тогда получается или ничего не дающее тождество (был сделан неправильный выбор множителей u и dυ) или такое равенство, из которого удается найти выражение для искомого интеграла.

Пример 13. Вычислить интеграл Подынтегральное выражение содержит единственную функцию coslnx, поэтому

u = coslnx
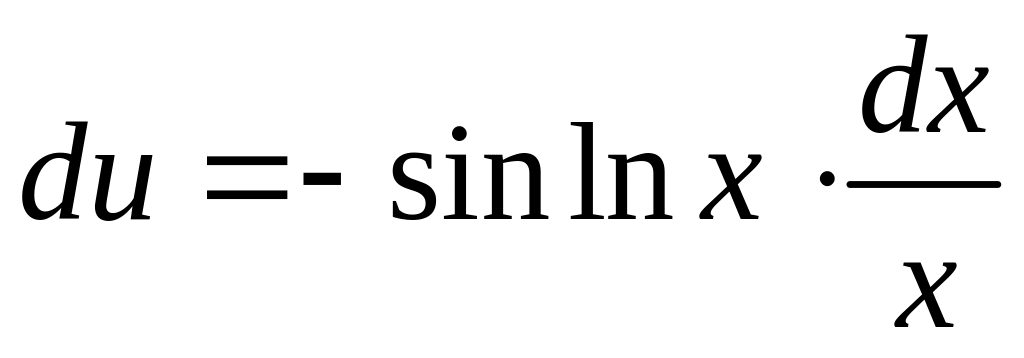
dυ =dx	υ = x

По формуле (3.3.1) получим Ко второму интегралу еще раз применим интегрирование по частям

u = sinlnx
dυ =dx	υ = x

Тогда

Двойное интегрирование по частям привело к исходному интегралу т.е.

I = x(coslnx + sinlnx) – I

Перенесем его в левую часть последнего равенства

2I = x(coslnx + sinlnx),

отсюда исходный интеграл будет равен

Таким же способом вычисляют интегралы и некоторые другие, они получили название циклических. Последние два интеграла можно занести в таблицу интегралов. Для них найдены следующие формулы.

1.

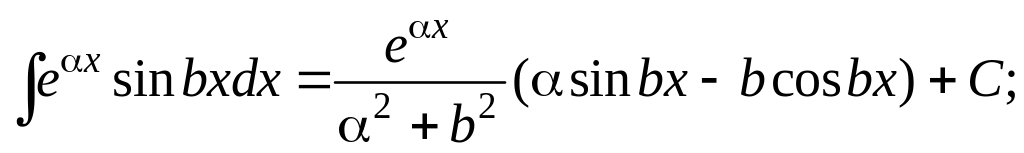
2.

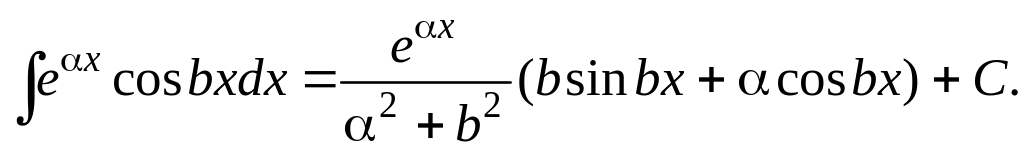
Пример 14. Найти Здесь α = –2; b = 3, по

формуле (3.3.1) получим

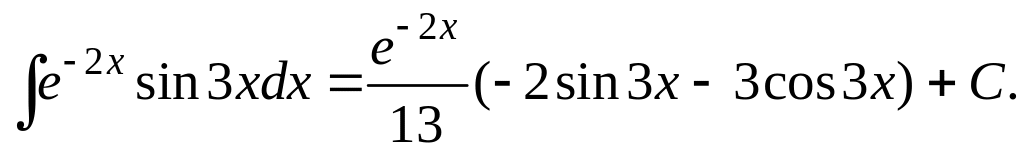
В процессе интегрирования очень важно правильно выбрать один из изложенных приемов, который привел бы заданный интеграл к табличному или уже знакомому.