3.2.4. Интегрирование подведение под знак дифференциала

Применение теоремы 2 об инвариантности формул интегрирования к нахождению первообразной называют методом подведения под знак дифференциала. Рассмотрим это на примерах.

Пример 10. Вычислить интеграл .

Выражение, стоящее под знаком радикала выберем в качестве новой переменной интегрирования t = x³ + 2, тогда dt = 3x²dx. В результате интеграл сведется к табличному от степенной функции:

Пример 11. Вычислить интеграл

Пусть t = x² + 1, dt = 2xdx, тогда

Итак, если под знаком интеграла стоит произведение двух функций, причем одна из них является производной от второй или её промежуточного аргумента, то за переменную интегрирования можно взять функцию, производная от которой стоит под знаком интеграла, преобразовав соответственно дифференциал. Подведение производной под знак дифференциала и интегрирование по функции значительно расширяет основную таблицу интегралов.

Приведем еще несколько примеров.

Вычислить интегралы

Пример 12.

Возвращаясь к переменной х получим

Пример 13.

Пример 14.

Вывод. В данной лекции были рассмотрены понятия первообразной функции, неопределенного интеграла, его свойства и геометрический смысл. Приведена таблица простейших интегралов и основные правила нахождения первообразных.

Лекция 3.3. Итегрирование заменой переменных. Интегрирование по частям. Многочлены и их свойства. Разложение на линейные квадратные множители

3.3.1. Замена переменной (метод подстановки)

При отыскании некоторых интегралов мы уже пользовались методом подстановки, применяя теорему 2 об инвариантности формул интегрирования. Если подынтегральное выражение удавалось записать в виде

где t = φ(x) и интеграл от выражения справа известен, т.е.:

то исходный интеграл был равен

С помощью этого приема можно найти следующие интегралы.

Пример 1. Найти Так как d(x²)=2xdx,

положим t = x²; dt = 2xdx, тогда

Пример 2. Дифференциал d(x⁴)=4x³dx, поэтому сделаем замену t = x⁴; dt = 4x³dx, отсюда

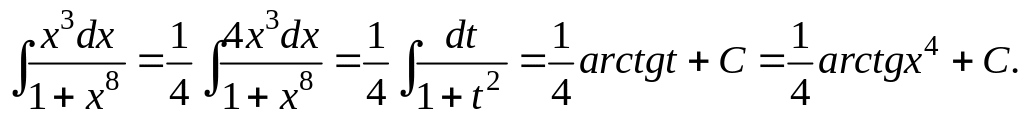
Пример 3. Под знаком интеграла есть производная от sinx. Пусть z = sinx; dz = cosxdx, имеем

Если подынтегральная функция такова, что трудно выделить производную от какого либо промежуточного аргумента или его просто нет, то в этом случае переменную интегрирования лучше заменить некоторой другой функцией, полагая х = (t); dx = '(t)dt, (предполагается, что (t) и '(t) непрерывны). Тогда

Если последний интеграл в результате такой замены свелся к табличному и равен F(t) + C, то заданный интеграл определяют путем возвращения к переменной х, т.е. из уравнения х = (t) надо найти обратную функцию t = φ(х), и заменить t на φ(х).

С помощью подстановок такого рода удается избавится от корня, упростить подынтегральную функцию и свести интеграл к табличному. Однако, общего рецепта для выбора функции (t) нет. В каждом конкретном случае её подбирают индивидуально по виду подынтегрального выражения. Все дальнейшее изложение темы «Неопределенный интеграл» будет состоять в основном из рассмотрения различных подстановок. Приведем несколько примеров.

Пример 4. Найти В данном интеграле нужно избавится от корня. Положим , тогда х = t²+1; dx=2tdt, интеграл примет вид

.

Заменяя t выражением , окончательно получим

Пример 5. Найти Положим

В результате такой замены интеграл сводится к табличному.

где Заменяя t выражением , окончательно получим

(можно было сделать подстановку х = tgt).

Пример 6. Вычислить В данном интеграле также нужно избавиться от корня. Для этого оказывается удобной замена

Выражение преобразуется так:

Интеграл примет вид:

где возвращаясь к переменной х, получим:

Приведенные примеры показывают, что успех интегрирования зависит от того, сумеем ли мы подобрать такую удачную замену переменной интегрирования, которая упростила бы данный интеграл.