3.2.2. Простейшие правила интегрирования

Простейшие правила нахождения первообразных основаны на следующих свойствах неопределенного интеграла.

Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции

Свойство 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению. В самом деле:

Свойство 3. Неопределенный интеграл от дифференциала функции равен самой функции плюс постоянная.

Из второго и третьего свойств следует, что символы дифференциала и неопределенного интеграла уничтожают друг друга, будучи примененными последовательно (если отвлечься от постоянного слагаемого в последней формуле).

Свойство 4. Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций:

(3.2.2)

где u, υ,…,ω – функции независимой переменной х.

Свойство 5. Постоянный множитель подынтегральной функции можно вынести за знак интеграла, т.е.:

(3.2.3)

где С – константа.

Пример 4. Вычислить интеграл

Применяя свойства интеграла, получим:

Хотя каждое промежуточное интегрирование дает произвольное постоянное слагаемое, но их сумма снова будет произвольной постоянной.

Теорема 2. (Об инвариантности формул интегрирования). Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е. если

то и

где t = φ(x) – любая дифференцируемая функция от х.

Доказательство. Пусть где F'(x) = f(x).

Возьмем теперь сложную функцию F[φ(x)] = F(t), у которой промежуточным аргументом является дифференцируемая функция t = φ(x). В силу теоремы об инвариантности (неизменности) формы первого дифференциала функции имеем:

dF(t) = F'(t)dt = f(t)dt

Отсюда

Таким образом, переменной интегрирования может быть любая функция от х. Теорема доказана.

В силу этого правила таблица интегралов оказывается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой дифференцируемой функцией от нее.

3.2.3. Таблица интегралов

1.

2.

2^а.

2^б.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16. или

17.

18.

19.

Таблица интегралов для элементарных функций выписана в предположении, что t может быть как независимой переменной, так и любой дифференцируемой функцией от х, т.е. t = φ(x).

Легко понять, что табличные интегралы можно было бы писать и в виде

3. 5. 6. и т.п.

Точно также интеграл можно записать в любом из видов Сказанное делает понятным назначение множителя dx. Он указывает на переменную интегрирования: x, t, z, u, y.

Операция интегрирования значительно сложнее дифференцирования. Интегрирование требует индивидуального подхода к каждой функции.

Вычислить неопределенные интегралы

Пример 5.

Все три интеграла табличные.

Пример 6.

Пример 7.

Пример 8.

Пример 9.

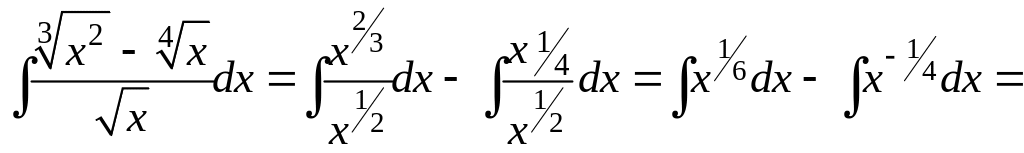
При нахождении первообразных использованы свойства неопределенного интеграла и алгебраические преобразования подынтегральной функции, в результате все интегралы свелись к табличным.