3.1.7. Возведение в степень

При возведении в целую положительную степень комплексного числа в показательной или тригонометрической форме его модуль возводится в эту степень, а аргумент умножается на данную степень.

Пусть тогда

или

Запишем результат возведения в целую степень в тригонометрической форме

Эту формулу называют формулой Муавра.

Пример 5. Вычислить

Решение. Перейдем к показательной форме. Найдем модуль и аргумент комплексного числа .

3.1.8. Извлечение корня

Извлечение корня n-ой степени из комплексного числа можно рассматривать как операцию возведения комплексного числа в дробную степень т.е. .

Если комплексное число в показательной форме, то

.

Придавая k – значения от 0 до n – 1 получим n – различных комплексных чисел, у которых модули одинаковые, а аргументы разные:

При k = 0

При k = 1

При k = 2

…………..

При k = n – 1

При k = n

Последнее значение аргумента числа совпадает с первым при k = 0.

Итак, корень n-ой степени из комплексного числа имеем n – различных значений.

Пример 6. Найти все значения корня .

Действительное число –1 можно рассматривать как комплексное, у которого действительная часть: α = –1, а мнимая β = 0, т.е.:

Запишем это число в тригонометрической форме. Для этого найдем его модуль и аргумент.

Т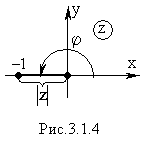 ак как tgφ = 0 при φ = 0 и φ = π, построим число «–1» на комплексной плоскости (Рис. 3.1.4), его аргумент равен

arg(–1) = φ = π

следовательно, тригонометрическая форма числа «–1» следующая:

.

Согласно формуле вычисления корня имеем:

.

К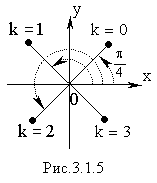 орень четвертой степени имеет четыре значения, которые можно найти, если положить к равным 0, 1, 2, 3.

При k = 0

При k = 1

При k = 2

При k = 3

Все четыре значения корня имеют одинаковы модули и отличаются друг от друга только значением аргумента (Рис.3.1.5).

Лекция 3.2. Первобразная и неопределенный интеграл. Геометрический смысл, свойства. Таблица простейших интегралов. Интегрирование подведением под знак дифференциала

3.2.1.Определение, геометрическая иллюстрация

Основной задачей дифференциального исчисления является задача нахождения дифференциала или производной данной функции, т.е. задача нахождения скорости изменения значений какой-нибудь функции, при изменении аргумента. На практике часто бывает важно решить обратную задачу: зная скорость изменения значений функции (по отношению к аргументу), найти эту функцию.

Так в механике по заданной скорости определяют закон движения материальной точки, а также закон изменения скорости (со временем) по заданному ее ускорению. Эти задачи приводят к проблеме отыскания функции по ее производной f(x). Неизвестная функция, обозначим ее F(x), получила название первообразной по отношению к своей производной.

Определение. Функцию F(x) называют первообразной для функции f(x) на числовом промежутке Х, если в любой его точке х она дифференцируема и имеет производную F'(x), равную f(x), т.е.

F'(x) = f(x).

Числовым промежутком мы будем называть множество точек числовой оси заключенных между двумя точками, и определяемых неравенствами:

α < x < b, α ≤ x ≤ b, α ≤ x < b, α < x ≤ b, – ∞ < x < ∞.

Пример 1. Функция является первообразной для функции на интервале (–1;1), так как в любой его точке х выполняется равенство:

Пример 2. Функция – есть первообразная для функции f(x)= cosx на интервале (–∞; ∞), ибо в каждой его точке х справедливо равенство:

(sinx)' = cosx.

Если F(x) является первообразной для функции f(x) на числовом промежутке Х, то и функция F(x) + С, где С – любая постоянная, также является первообразной для f(x) на Х. Действительно:

(F(x) + C)' = F'(x) + (C)' = F'(x) = f(x).

Следовательно, данная функция имеет бесконечное множество первообразных. Связь между различными первообразными для одной и той же функции f(x) выражена следующей основной теоремой.

Теорема 1. Две различные первообразные одной и той же функции, определенной в некотором промежутке Х, отличаются друг от друга в этом промежутке на постоянное слагаемое.

Пример 3. Функция f(x) = sinx · cosx имеет первообразные:

(проверьте).

Покажем, что разность между ними равна числу. Преобразуем функцию F₃(x):

т.е. или

Аналогично:

Таким образом, если F(x) – есть одна из первообразных для функции f(x) на числовом промежутке Х, то выражение F(x) + C, где С – произвольная постоянная, исчерпывает множество всех первообразных для f(x). (Предполагается, что рассматриваемые функции непрерывны на числовом промежутке Х).

Определение. Отыскание первообразных называют неопределенным интегрированием, а выражение, охватывающее множество всех первообразных от данной функции f(x) – неопределенным интегралом от f(x) и обозначают:

где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, х – переменная интегрирования.

Согласно данного определения, неопределенный интеграл записывают так:

, (3.2.1)

где F(x) – одна из первообразных (F'(x) = f(x)),

(F(x) + C) – множество всех первообразных.

График каждой из первообразных для функции y=f(x), называют интегральной кривой.

Если Y=F₁(x) и Y=F₂(x) – первообразные одной и той же функции f(x), то касательные к их графикам в точках с общей абсциссой х параллельны между собой:

(рисунок 3.2.1).

Р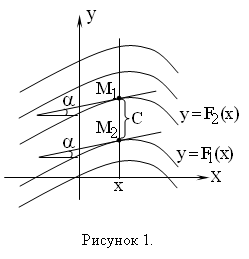 асстояние между этими кривыми, считая вдоль оси Oу, остается постоянным:

т.е. кривые в некотором смысле «параллельны» друг другу. Поэтому, неопределенный интеграл геометрически представляется множеством всех интегральных кривых, полученных при параллельном движении одной из них по направлению оси Oу.