3.11.13. Закон Архимеда

По закону Архимеда подъемная сила, действующая на погруженное твердое тело в жидкость, равна весу вытесненной им жидкости. Вес тела равен: P = S·H·d, где S – площадь поперечного сечения H – высота, d – удельный вес.

Задача. Шар радиуса R с удельным весом d = 1 погружен в воду так, что он касается поверхности. Какую работу надо затратить, чтобы извлечь шар из воды.

Р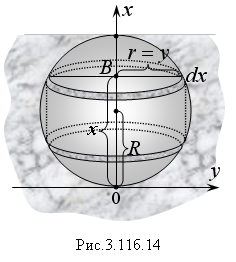 ешение. Фиксируем определенное значение х = ОВ, по приращению dx найдем работу, затраченную на поднятие цилиндра высотой dx на величину х.

Основанием цилиндра является круг, радиус которого r = y можно найти из уравнения окружности: Раскрывая квадрат получим:

отсюда

тогда

Работа, затраченная на поднятие шара из воды будет равна

В лекциях (3.11., 3.11а., 3.11б.) были рассмотрены две схемы применения определенных интегралов к нахождению геометрических и различных физических величин. Первая основана на приближенном представлении искомой величины в виде интегральной суммы с последующим переходом к пределу (вычисление площадей, длин линий, объемов тел, координат центров тяжести, моментов инерции и т.д.).

Вторая схема основана на составлении «элемента» (дифференциала) рассматриваемой величины.

Примеры на применение этой схемы к решению физических задач авторы старались отобрать так, чтобы облегчить дальнейшее применение интегрального исчисления к специальным дисциплинам.