3.1.3. Показательная форма записи комплексного числа

В математическом анализе в дальнейшем доказываются формулы, которые впервые были получены Эйлером. Доказательство этих формул основано на теории рядов, поэтому мы приводим их без доказательств.

По формулам Эйлера показательную функцию с мнимой единицей в показателе степени можно выразить через тригонометрические функции действительного аргумента следующим образом:

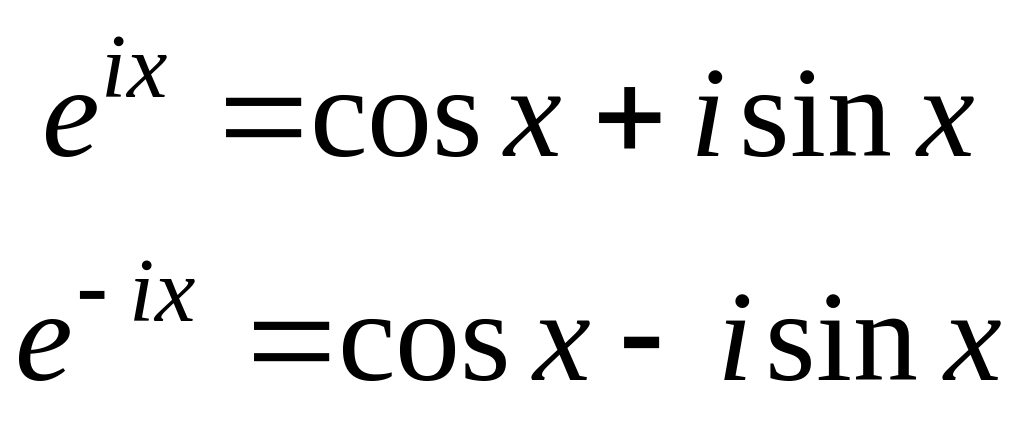(3.1.1)

Из формул Эйлера (3.1.1) легко получить другие:

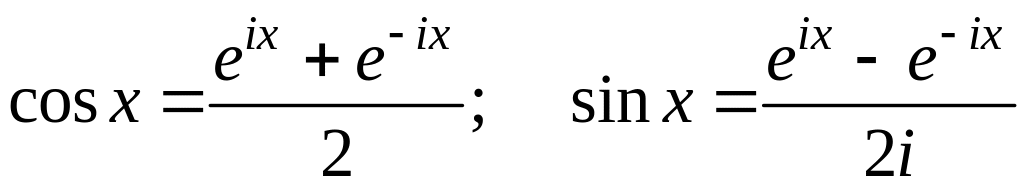
Запишем комплексное число в тригонометрической форме:

Выражение в скобках, согласно формуле Эйлера (3.1.1) представляет собой показательную функцию с мнимой единицей в показателе степени т.е.

Последнюю запись называют показательной формой комплексного числа.

Итак, комплексное число можно представить в трех формах:

– алгебраической

– тригонометрической

– показательной

Пример 1. Представить в алгебраической форме комплексное число .

Решение. Комплексное число дано в показательной форме, его модуль ,

аргумент . Найдем действительную и мнимую части:

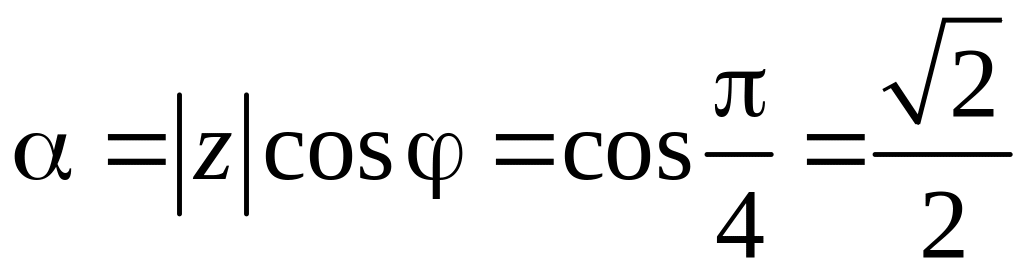
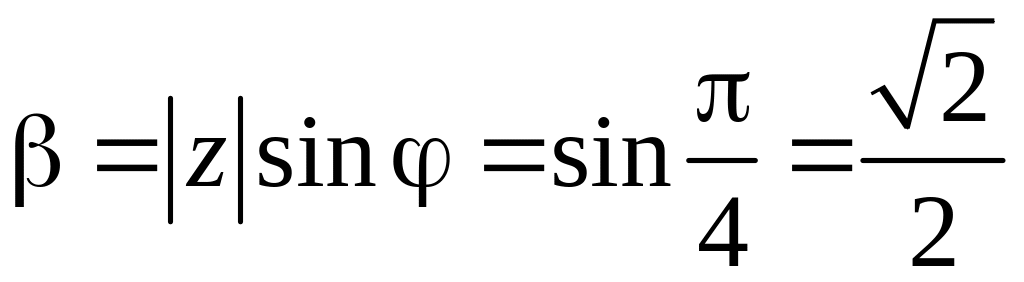
Таким образом .

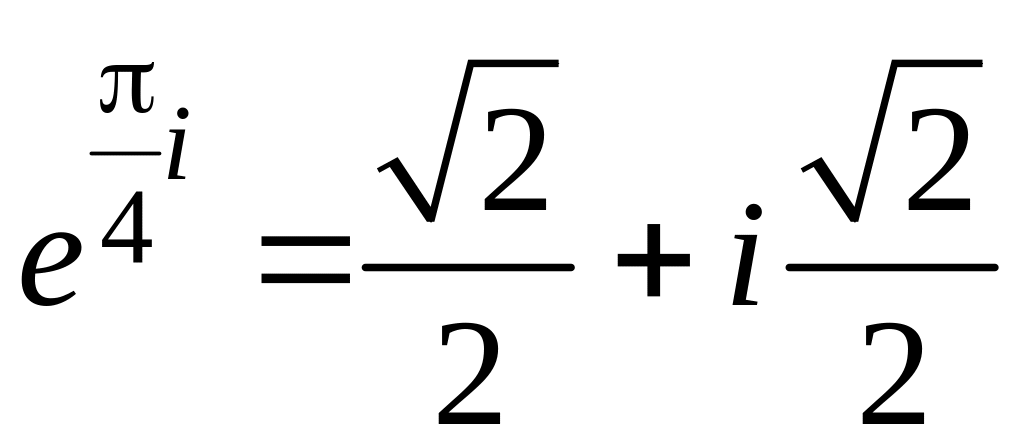Пример 2. Перейти от алгебраической к показательной форме комплексного числа z = – i.

Р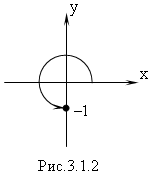 ешение. Для данного числа α =0; β = –1, найдем его модуль и аргумент:

(Рис.3.1.2)

Следовательно .

3.1.4. Действия над комплексными числами (сложение и вычитание)

О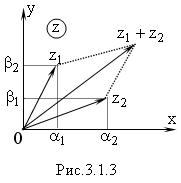 перацию сложения и вычитания комплексных чисел можно рассматривать как операцию сложения и вычитания векторов (Рис.3.1.3)

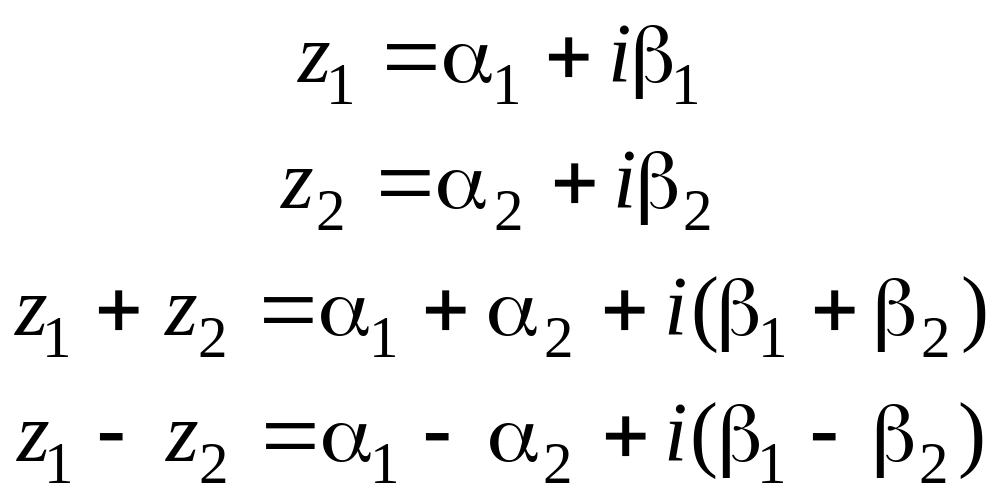
При сложении и вычитании комплексных чисел, их действительные и мнимые части складываются или вычитаются, при этом

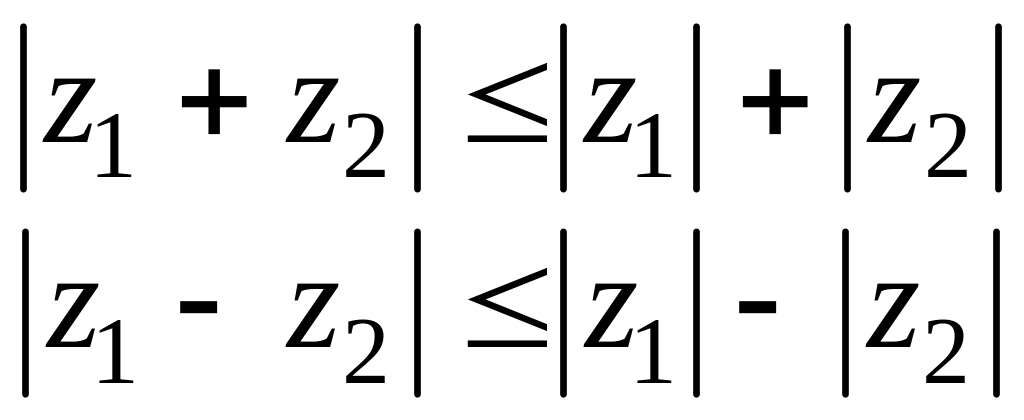
Пример 3. Найти , если

Сложение и вычитание комплексных чисел удобнее проводить, когда они записаны в алгебраической форме.

3.1.5. Умножение комплексных чисел

Рассмотрим умножение комплексных чисел в алгебраической форме.

Даны два числа:

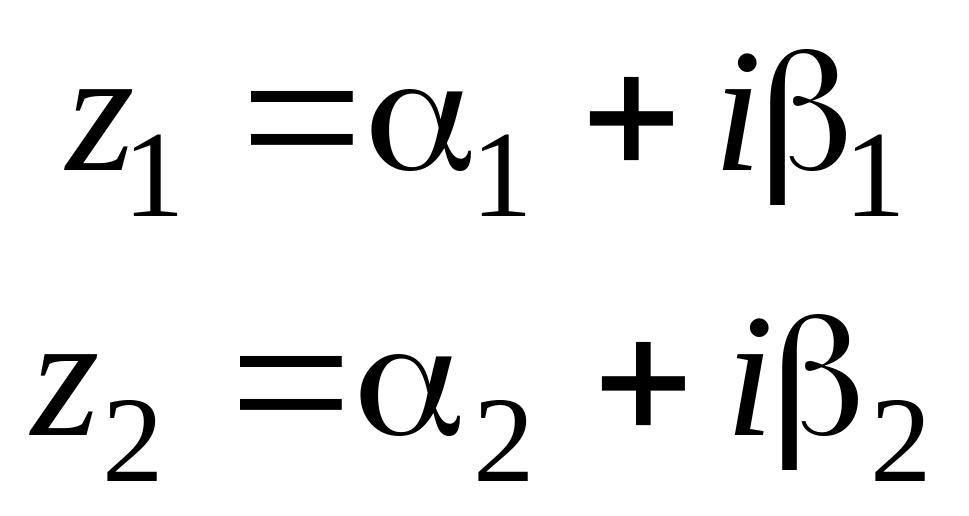
Нужно найти произведение .

Перемножим двухчлены по правилам алгебры:

если учесть, что то получим:

Таким образом, умножение комплексных чисел в алгебраической форме проводится по обычным алгебраическим правилам.

Следует отметить, что произведению сопряженных комплексных чисел является действительным числом, в самом деле

Пусть комплексные числа даны в показательной форме

Найдем их произведение

Складывая показатели степени у показательных функций с одинаковым основанием, получим:

По формулам Эйлера (3.1.1) результат перемножения двух комплексных чисел можно записать в тригонометрической форме:

Итак, при умножении комплексных чисел в показательной и тригонометрической формах модули перемножаются, а аргументы складываются.

3.1.6. Деление комплексных чисел

Деление комплексных чисел, так же как и умножение, удобнее вводить, когда они записаны в показательной или тригонометрической форме.

Найдем частное от деления двух комплексных чисел:

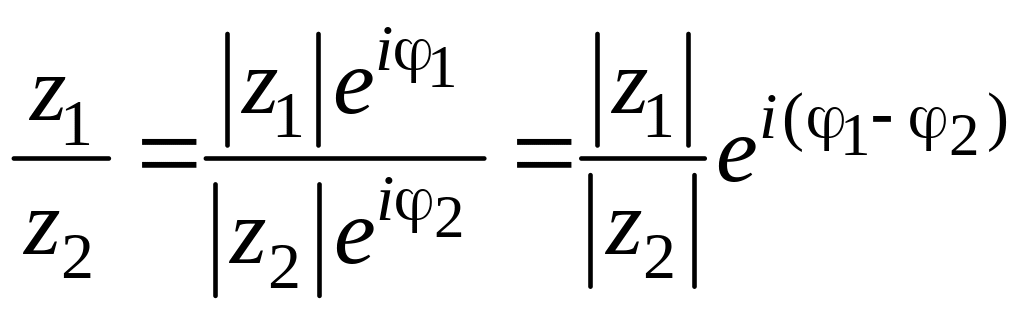или

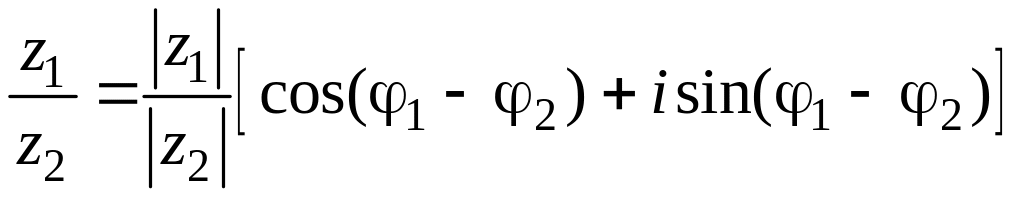
Таким образом, при делении комплексных чисел их модули делятся, а аргументы вычитаются.

Деление комплексных чисел можно проводить и в алгебраической форме. Найдем частное от деления:

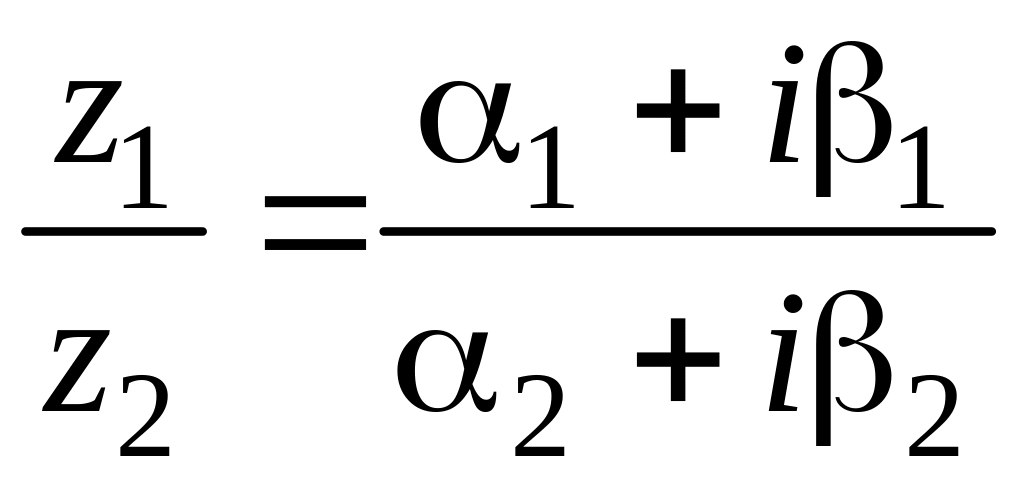
Чтобы избавится от мнимой единицы в знаменателе, нужно умножить числитель и знаменатель на сопряженное число знаменателю:

а затем по обычным правилам алгебры перемножить двухчлены

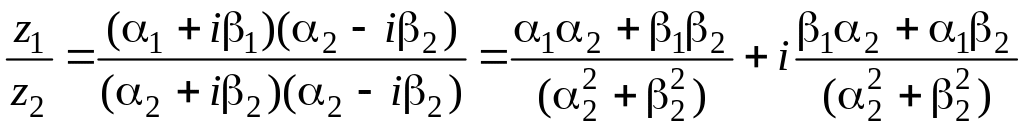
Полученный результат также является комплексным числом в алгебраической форме.

Пример 4. Вычислить

Решение. Умножим числитель и знаменатель на сопряженное число знаменателю 1 – i:

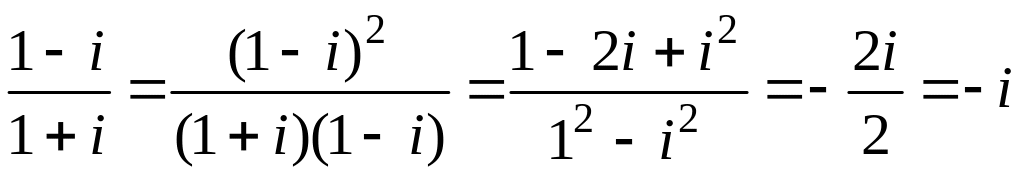
Такой же результат получается при переходе к показательной форме
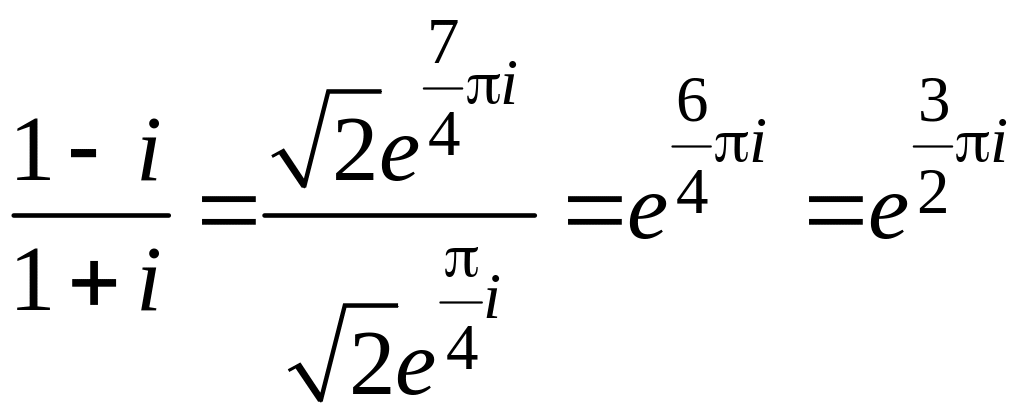