3.11.6. Общая схема применение линейного интеграла к физическим задачам.

Решение задач на применение определенного интеграла можно осуществить двумя способами. Первый способ опирается на непосредственное определение определенного интеграла как предела интегральной суммы.

Искомая величина (масса неоднородного стержня, площадь, работа и т.д.) соответствовала некоторому отрезку [α,b] изменения величины х, которая служит переменной интегрирования. Определяемая величина обладает свойством аддитивности. Первый шаг состоит в разбиении отрезка [α,b] на частичные интервалы где i = 0,1,2,…, n – 1, x₀ = α, x_n = b.

Далее составляют интегральную сумму, выражающую приближенное значение искомой величины, тем более точное, чем меньше наибольшая из длин частичных интервалов

Переходя к пределу при находят искомую величину в виде интеграла

(3.11б.1)

где f(x) – данная по условиям задачи функция (плотность, ордината линии, ограничивающей трапецию, действующая сила и т.д.). Точно так же может быть решена и всякая другая задача аналогичного типа.

Второй путь решения исходит из окончательного результата, т.е. предполагается, что искомая величина равна линейному интегралу от некоторой функции, взятому по определенному отрезку.

П усть интересующая нас величина рассматривается на переменном интервале [β,x] с фиксированным левым концом β(β ≤ α).

Тогда эта величина будет некоторой функцией u = F(x) от абсциссы х. Если бы функция F(x) была известна, то легко найти значение искомой величины J соответствующей отрезку [α,b]. Это наглядно видно на примере площади криволинейной трапеции (Рис.3.11б.1)

Здесь искомая величина

и в силу свойства аддитивности F(b) = F(α) + J, отсюда J = F(b) – F(α).

Функция F(x) дифференцируема; по формуле Ньютона-Лейница имеем

Искомая величина измеряется интегралом от дифференциала функции u = F(x), взятому по отрезку [α,b].

Подынтегральное выражение f(x)dx в формуле (3.11б.1) есть не что иное, как дифференциал du функции u = F(x). Поэтому, для решения задачи достаточно знать не саму функцию F(x), а только ее дифференциал, который можно найти из условия задачи. Для этого в произвольной точке х заданного отрезка [α,b] берется бесконечно малое приращение dx и находится соответствующее ему приращение ΔF(x). Та часть этого приращения, которая получилась бы, если все другие величины, определяющие образование F(x) сохраняют в отрезке [x,x + Δx] свои значения, принятые в точке х, и оказывается дифференциалом dF(x).

То, что полученное выражение является дифференциалом, можно проверить убедившись в том, что оно во-первых, пропорционально dx, а во-вторых, отличается от ΔF(x) на бесконечно малую величину более высокого порядка, чем dx, или найти предел отношения полученного выражения к ΔF(x) при dx → 0, который должен быть равен единицы.

Рассмотрим решение некоторых задач физики описанным методом.

3.11.7. Давление жидкости на стенку сосуда

а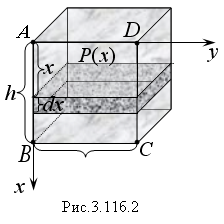 ) Пусть жидкость заполняет сосуд прямоугольного параллелепипеда с удельным весом γ Н/м³. Подсчитаем давление Р на стенку сосуда ABCD, где AB = h, BC = α. Зафиксируем произвольное значение х, обозначим давление на заштрихованную часть стенки через Р(х) (Рис.3.11б.2).

Изменим х – на величину dx и найдем главную часть приращения давления, пропорциональную dx. Будем считать, что на выделенной полоске глубина жидкости не меняется и равна х.

Так как давление жидкости на малую площадку равно произведению удельного веса на площадь и глубину погружения, то

Если глубину погружения принять равной , приращение давления на стенку сосуда будет равно .

Легко видеть, что предел отношения ΔР(х) к dP(x) равен единицы и dP(x) действительно является дифференциалом функции Р(х):

Интегрируя в пределах от 0 до h, получим

б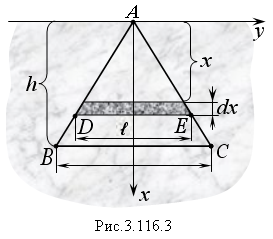 ) Пусть в воду (γ = 1) опущен треугольный щит, так что основание треугольника параллельно свободной поверхности воды, а вершина находится на этой поверхности.

Чтобы найти давление Р воды на щит, выделим полоску шириной dx на глубине х и вычислим dP(x). Длину ℓ элементарной площадки найдем из подобия треугольников ABC и ADE: так что а площадь будет равна

Тогда Отсюда

Рассуждая аналогично, можно найти давление воды на треугольный щит повернутый вершиной вниз, а основание ВС находится на уровне свободной поверхности. В этом случае давление уменьшается вдвое (проверьте) и будет равно Так можно найти давление на пластинку любой формы, опущенную в жидкость.