3.11.5. Момент инерции
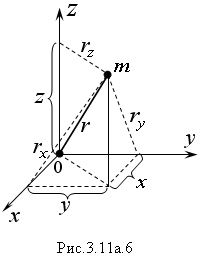
Моментом инерции материальной точки относительно начала координат или координатной оси называют произведение массы точки на квадрат ее расстояния до начала координат или оси (рис. 3.11а.6):
(3.11а.5)
Момент инерции системы точек (относительно одного и того же центра или оси) равен сумме моментов точек системы.
При непрерывном распределении масс по стержню, пластине или телу вместо суммы появляется интеграл линейный, криволинейный, двойной, поверхностный или тройной.
Формулы для моментов инерции различных неоднородных фигур с заданной плотностью ρ = ρ(Р) получаются так же, как формулы для статических моментов и координат центров тяжести. Предлагаем вывести их самостоятельно.
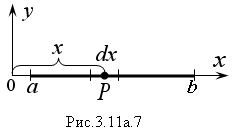
Моменты инерции прямого неоднородного стержня (Рис.3.11а.7) равны:
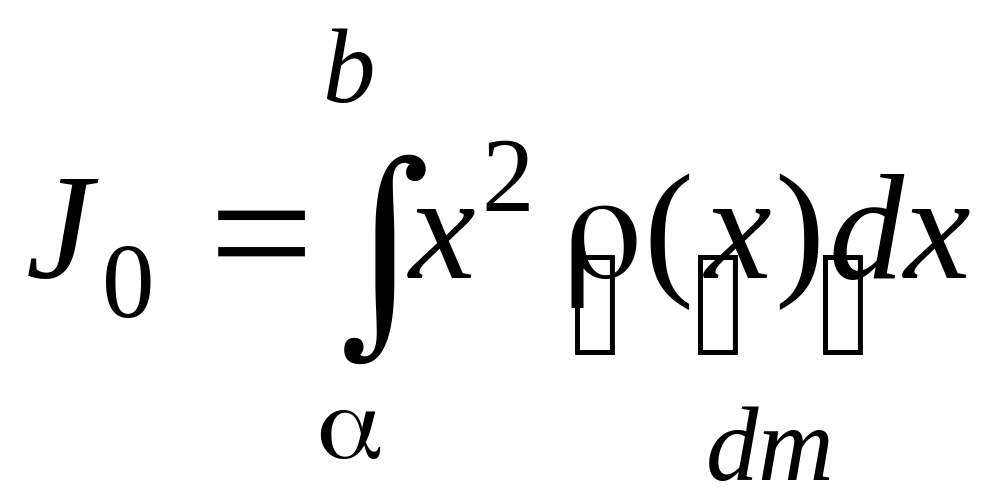
(3.11а.6)
Моменты инерции кривого неоднородного стержня (Рис.3.11а.8) определяют по формулам:
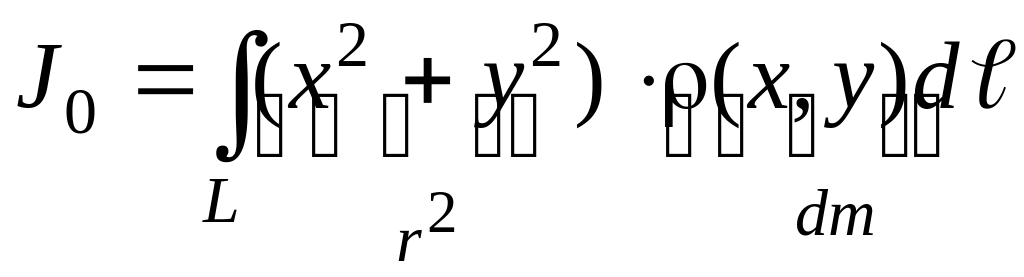
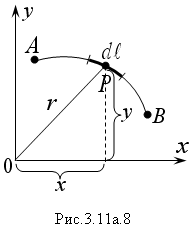
(3.11а.7)
Моменты инерции плоской пластины (Рис.3.11а.9) равны:
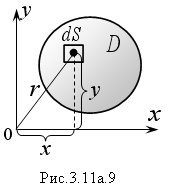
(3.11а.8)
Моменты инерции неоднородной изогнутой пластины (Рис.3.11а.10) задают выражениями:
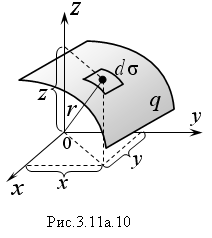
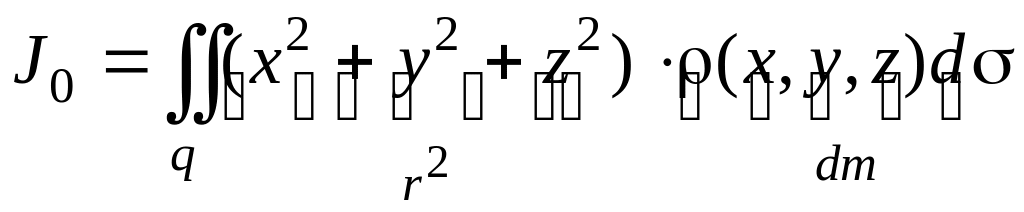
(3.11а.9)
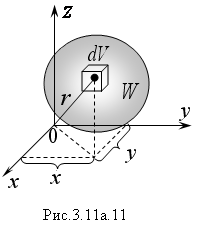
Моменты инерции неоднородного тела W (Рис.3.11а.11) равны тройным интегралам вида:
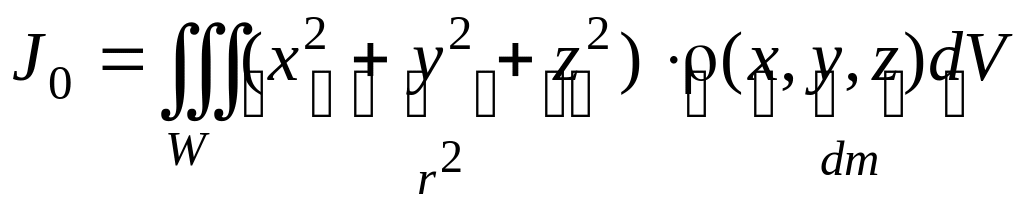
(3.11а.10)
Приведем два примера на вычисление моментов инерции.
Пример 4. Найти момент инерции относительно оси Oх однородной плоской линии, которая является верхней частью окружности
Решение.
Так как линия однородна, то линейная
плотность массы постоянна, т.е.
Согласно
формул (3.11а.7), момент инерции данной
линии относительно оси Ох
равен криволинейному интегралу по
верхней части окружности:
.
Перейдем к линейному интегралу. Для
этого выразим дифференциал длины dℓ
через уравнение линии
по формуле:
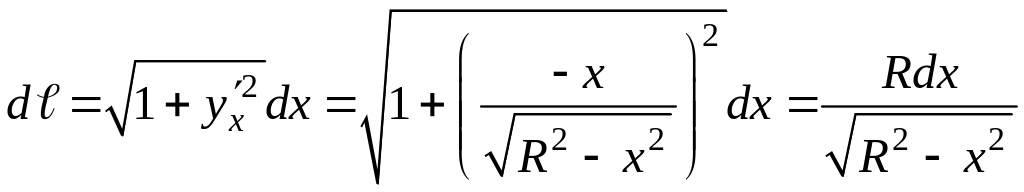
В криволинейном интеграле переменную y заменим ее зависимостью от x из уравнения данной окружности и подставим вместо dℓ найденное для него выражение, тогда
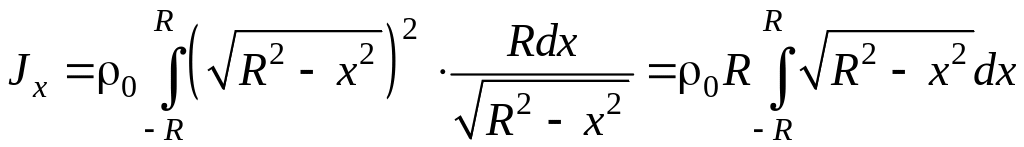
Полученный линейный интеграл является табличным. Применяя формулу Ньютона-Лейбница, найдем Jx:
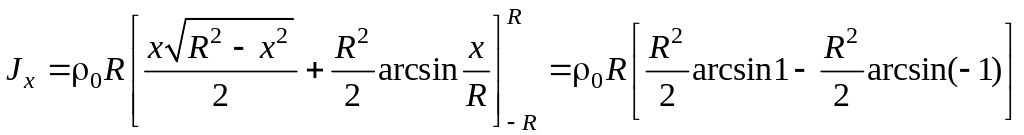
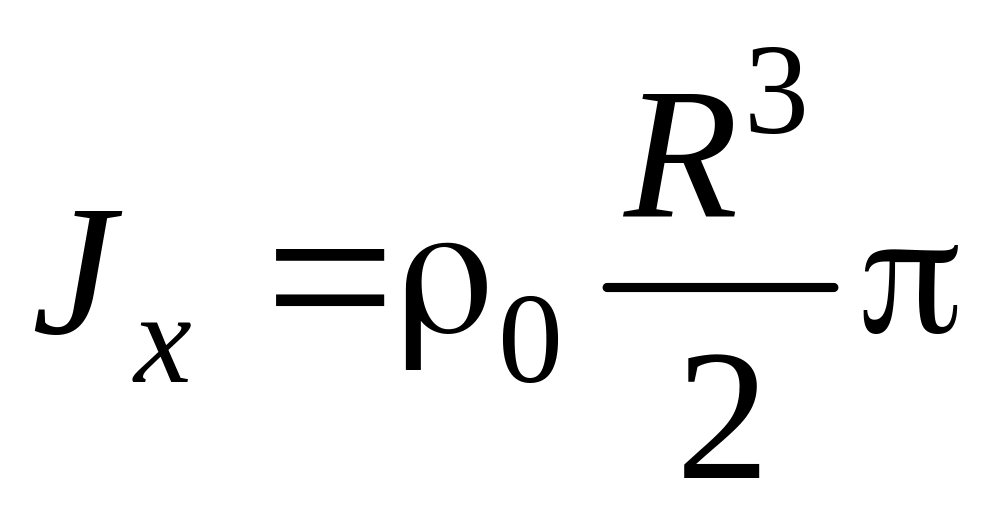
Уравнение
окружности
можно было взять в параметрической
форме:
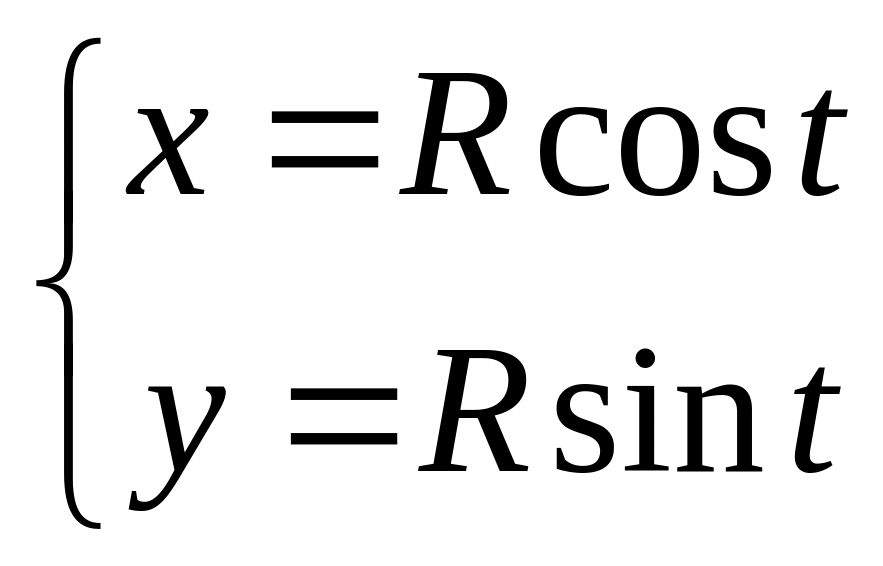
В этом случае дифференциал длины dℓ выражают через уравнение линии по формуле:
Параметр t в верней части окружности изменяется от 0 до π.
Переходя к линейному интегралу по переменной t, получим
Найденное значение для Jx такое же.
П
ример
5. определить
момент инерции однородного цилиндра
относительно оси Оz.
Высота цилиндра равна h
см, внутренний радиус – α
см, а внешний – b
см (Рис. 3.11а.12).
Решение. Так как цилиндр однородный, то плотность массы постоянна
Момент инерции относительно оси Оz найдем используя формулы (3.11а.10):
В тройном интеграле перейдем к цилиндрической системе координат:
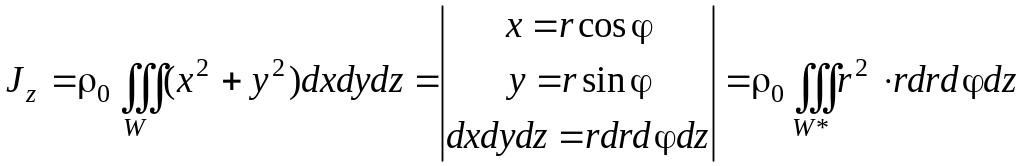
Значения переменных φ, r, и z внутри области W заключены в пределах
0 ≤ φ ≤ 2π; α ≤ r ≤ b; 0 ≤ z ≤ h.
Переходя к трехкратному интегрированию, получим:
Определение моментов инерции плоских тел и частей поверхностей относительно начала и осей координат приводит к вычислению двойных и поверхностных интегралов соответственно.