3.11.4 Статические моменты и центры тяжести

Р ассмотрим систему материальных точек на плоскости (рис. 3.11а.1). Произведение массы точки на ее расстояние до какой-нибудь оси называют статическим моментом точки относительно этой оси, обозначают:

Статический момент системы материальных точек равен сумме статических моментов точек, входящих в эту систему

За центр тяжести системы принимают такую точку с координатами (x_c,y_c), в которую нужно поместить всю массу системы, чтобы статический момент этой точки был равен статическому моменту системы, т.е.

(3.11а.1)

Отсюда получают формулы для нахождения координат центра тяжести системы материальных точек, расположенных на плоскости:

Аналогично, вычисляют координаты центра тяжести системы материальных точек в пространстве. В этом случае статические моменты системы точек определяют относительно координатных плоскостей:

(3.11а.2)

Найдем координаты центров тяжести неоднородных фигур пяти типов: прямого стержня [α,b], кривого стержня L, плоской пластины D, изогнутой пластины q и тела W. Все фигуры с данными размерами расположим определенным образом в декартовой системе координат. Будем считать, что распределение плотности массы в каждой фигуре известно и задано функцией:

ρ = ρ(Р)

где Р – точки, принадлежащие фигурам (рис.3.11а.2).

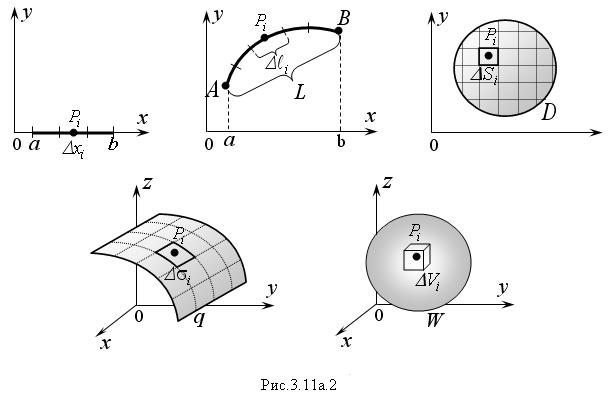
Разобьем все фигуры на n – частей. Меры элементарных частей обозначим: – соответственно.

В каждой элементарной части возьмем произвольную точку P_i и найдем в ней значение плотности массы:

ρ_i = ρ(P_i)

Сделаем два допущения. Во-первых, плотность распределения массы внутри каждой элементарной части постоянна и равна ρ(P_i). Во-вторых, вся масса сосредоточена в точке P_i.

Тогда все пять фигур можно рассматривать как системы, состоящие из n – материальных точек. Массы точек в этих системах будут соответственно равны:

Для прямого стержня [α,b]:

Для кривого стержня L:

Для плоской пластины D: (3.11а.3)

Для изогнутой пластины q:

Для объемного тела W:

Следовательно, координаты центров тяжести указанных фигур приближенно можно вычислить по формулам (3.11а.1) и (3.11а.2), если вместо масс точек подставить найденные для них значения из равенств (3.11а.3).

Точное значение координат центров тяжести получится, если перейти к пределу при стягивании элементарных частей в точку, а это приводит к интегрированию. Для каждой фигуры центры тяжести будут равны:

(3.11а.4)

Рассмотрим несколько примеров на применение полученных формул.

Пример 1. Найти координаты центра тяжести однородной линии ρ(x,y)= const = 1, которая является полуокружностью, расположенной над осью Oх, L: x² + y² = α²; y ≥ 0.

Р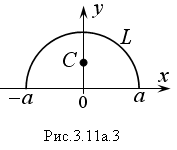 ешение. Поскольку кривая L (рис. 3.11а.3) симметрична относительно оси Oy, то центр тяжести лежит на этой оси, т.е. х_с = 0. вторую координату y_с найдем по формуле:

От криволинейных интегралов прейдем к линейным. Для этого выразим дифференциал длины dℓ через уравнение верхней части окружности :

Статический момент относительно оси Oх будет равен:

Найдем массу материальной кривой L

Подставляя верхний и нижний пределы для переменной x, окончательно получим

M_x = α[arcsin1 – arcsin(-1)] = απ

Таким образом, координаты центра тяжести данной линии равны

П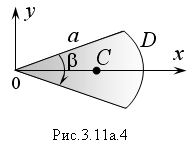 ример 2. Найти координаты центра тяжести сектора однородного круга радиуса α с центральным углом β, расположенного симметрично относительно оси Oх.

Решение. В силу симметрии центр тяжести плоского сектора D (рис. 3.11а.4) лежит на оси Oх, следовательно y_c = 0. Координату х_c найдем по формуле:

Пусть поверхностная плотность массы однородного сектора D равна ρ(x,y) = ρ₀. Вычислим его статический момент относительно оси Oy:

Так как плоская область D является круговым сектором, в двойном интеграле, перейдем к полярным координатам:

Значения переменных r и φ внутри D заключены в пределах

Переходя к двукратному интегрированию, получим:

Аналогично вычислим массу сектора D:

Переходя к двукратному интегрированию по переменным r и φ, найдем:

Координаты центра тяжести однородного сектора D будут равны:

Пример 3. Найти координаты центра тяжести шара

x² + y² + z² ≤ 2Rz,

если плотность массы в любой его точке равна квадрату расстояния от начала координат.

Решение. Центр шара смещен вверх по оси Оz на R единиц (рис. 3.11а.5), по условию задачи плотность массы задана функцией:

ρ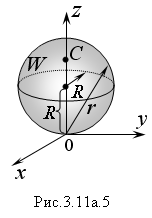 (x,y,z) = x² + y² + z² = r²

В силу симметрии центр тяжести шара расположен на оси Oz, следовательно х_с = 0, y_c = 0. Найдем координату z_c, используя формулы (3.11а.4).

В тройных интегралах перейдем к сферическим координатам. Сначала вычислим массу шара.

Значения переменной r внутри шара изменяются от 0 до ее значений на сфере x² + y² + z² = 2Rz, уравнение которой в сферической системе имеет вид:

Переменные Θ и φ изменяются в пределах:

Переходя к трехкратному интегрированию, найдем массу шара

Вычисляя последний интеграл, окончательно получим:

Найдем статический момент относительно координатной плоскости xOy:

Расставляя пределы изменения переменных r, Θ, φ и переходя к трехкратному интегрированию, получим:

Координаты центра тяжести неоднородного шара равны:

Центр тяжести, как и следовало ожидать, расположен в верхней части шара.