3.11.2. Вычисление длин линий

Длину плоских кривых, заключенных между двумя точками А и В, можно найти с помощью криволинейного интеграла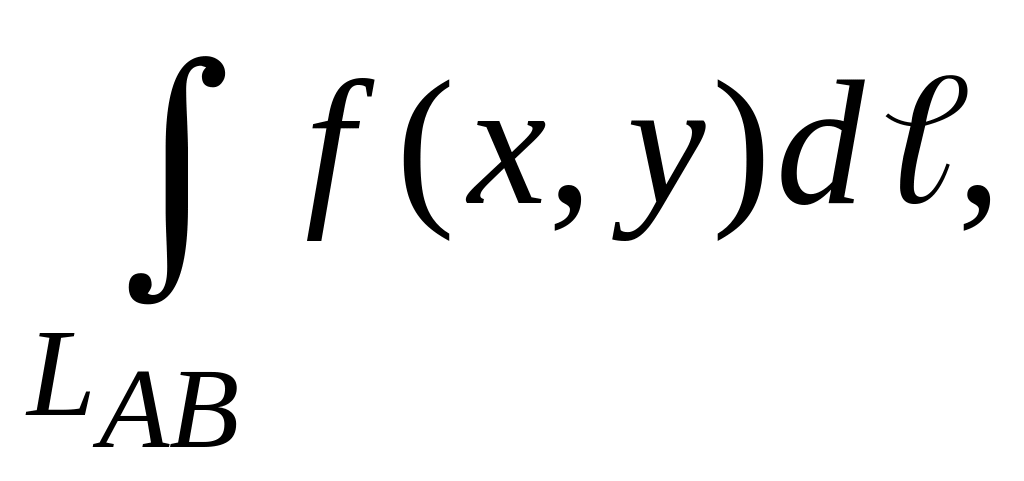 если положить f(x,y) ≡ 1. В этом случае криволинейный интеграл, также как и двойной, будет равен размерам области интегрирования, т.е. длине части линии L_AB.

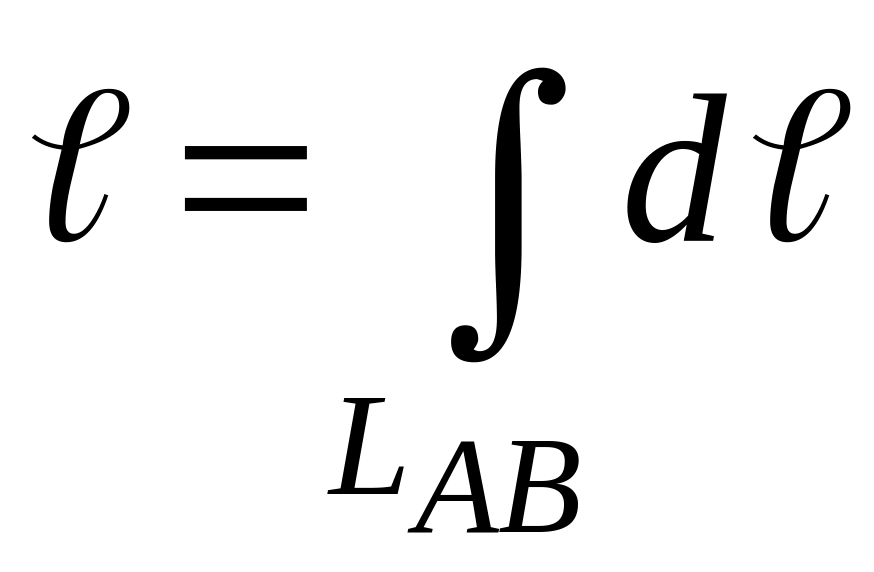
Меру элементарной части (дифференциал длины) - dℓ выражают через уравнение данной линии L_AB и переходят к линейному интегралу. Если кривая L_AB задана в декартовой системе координат непрерывной и дифференцируемой функцией y = y(x), то вычисление ее длины сводят к вычислению линейного интеграла вида:

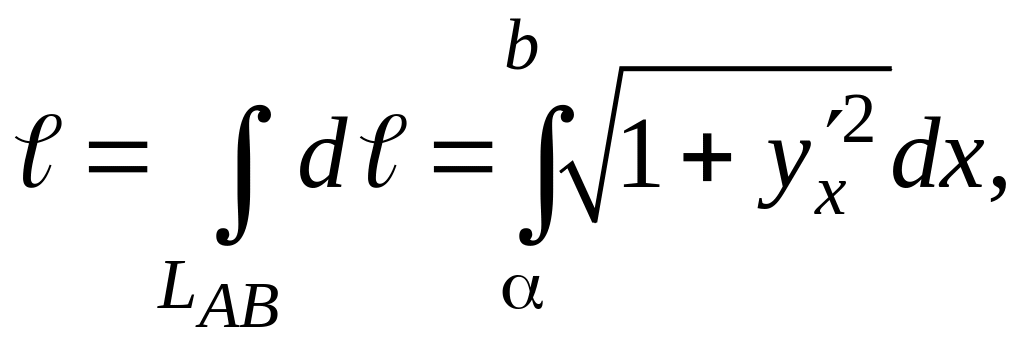где

Пределы в линейном интеграле α и b – являются проекциями на ось Oх точек линии А и В соответственно.

Длину дуги АВ кривой, заданной параметрическими уравнениями x = x(t); y = y(t), находят по формуле

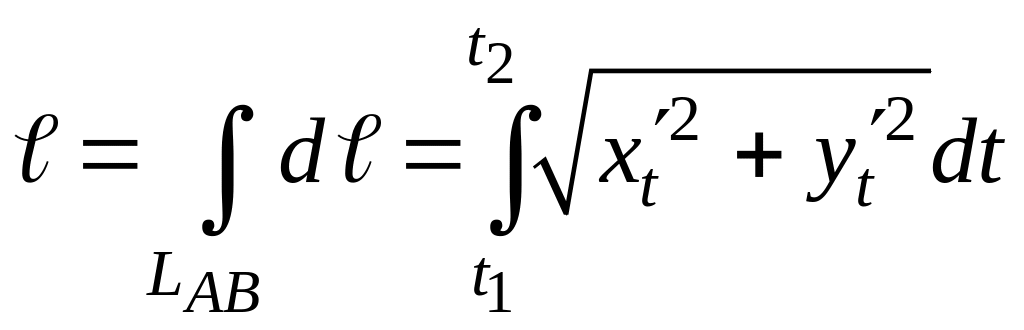
где t₁ и t₂ значения параметра t в точках А и В.

И наконец, длина линии L_AB, уравнение которой r = r(φ) задано в полярной системе координат, равна линейному интегралу

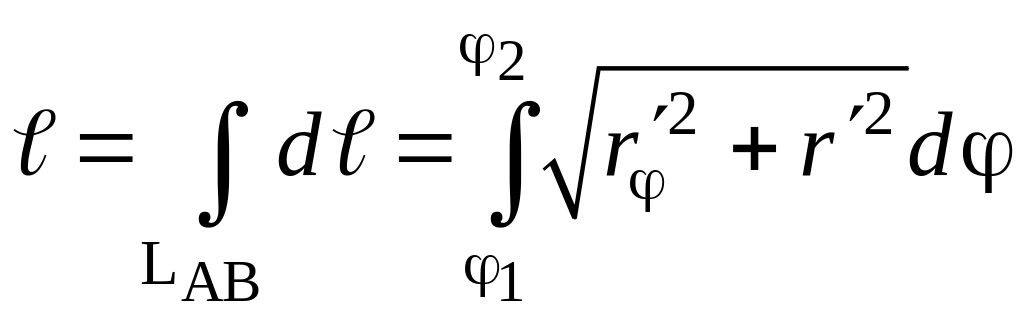
где φ₁ и φ₂ полярные углы точек А и В.

Пример 5. Найти длину полукубической параболы y² = x³ от точки А(0,0) до точки В(4;8).

Решение. Длина отрезка полукубической параболы между точками А и В равна криволинейному интегралу

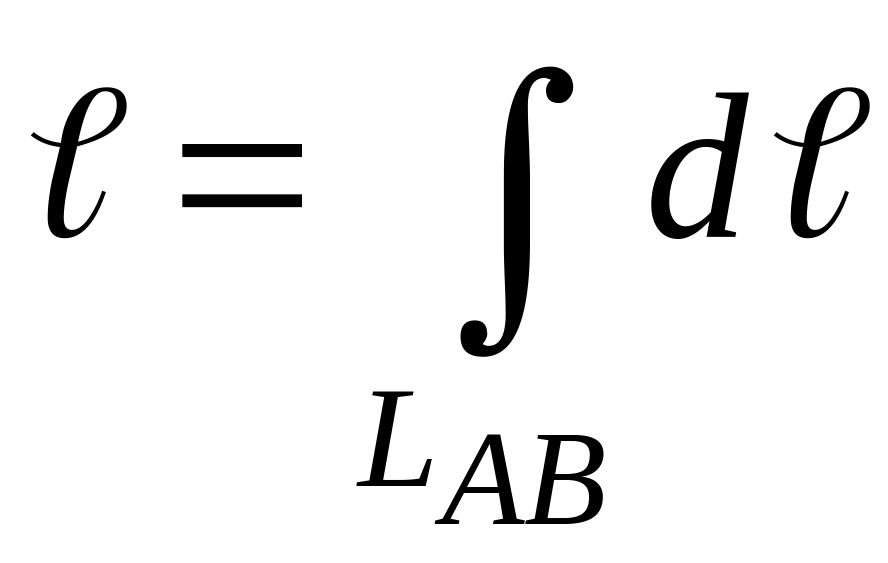
Дифференциал длины кривой в декартовой системе координат выражают через ее уравнение y = y(x) по формуле

Найдем его для данной линии

Переход от криволинейного интеграла к линейному и вычисление последнего дает искомую длину:

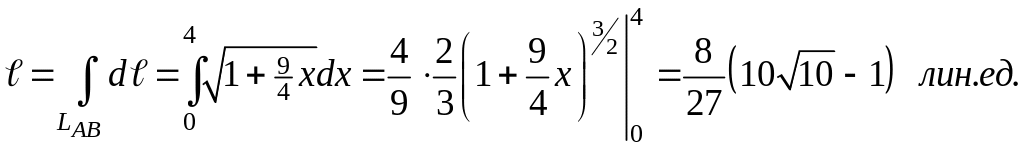
Пример 6. Найти длину астроиды, заданную параметрическими уравнениями

Решение.

Длину астроиды также найдем с помощью криволинейного интеграла

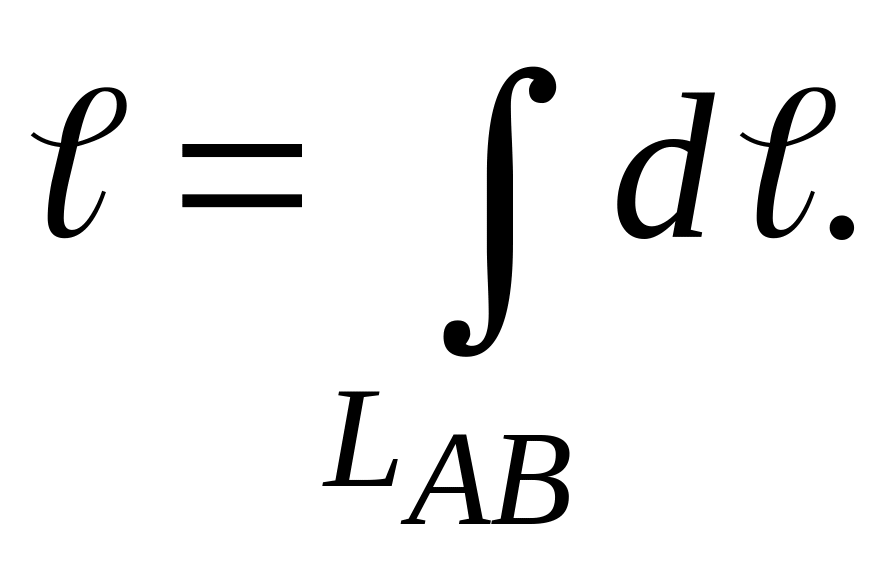
Дифференциал длины кривой, заданной параметрически, выражают через ее уравнение по формуле

Найдем его для астроиды

Подставляя найденное выражение для dℓ в криволинейный интеграл и переходя к линейному, получим:

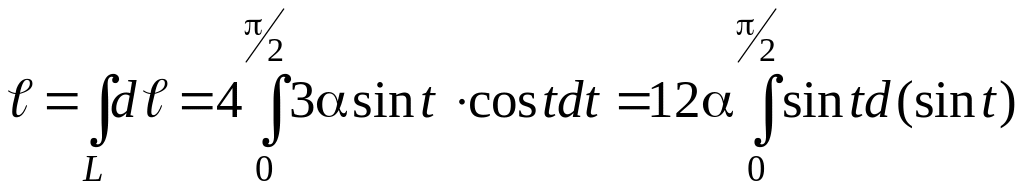
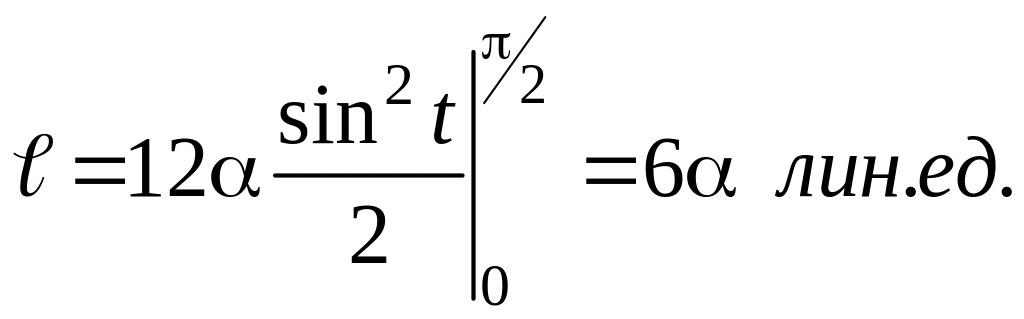
3.11.3.Вычисление объемов тел

Объем тел, в зависимости от их формы и условий задачи, можно находить различными способами.В частом случае, когда известна площадь поперечных сечений тела, его объем вычисляют с помощью линейного интеграла по формуле:

где S(x) – площадь сечения тела плоскостью, перпендикулярной оси Ox, α и b – проекции его крайних точек на ту же ось.

Исходя из этой формулы, находят объем тел вращения.

П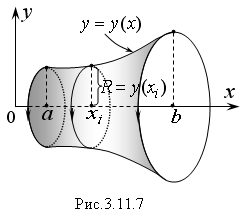 усть криволинейная трапеция, ограниченная сверху графиком непрерывной функции y = y(x) и прямыми x = α, x = b, вращается вокруг оси Oх (Рис. 3.11.7).

В результате ее вращения образуется тело. Его плоскими сечениями, перпендикулярными оси Oх, являются круги с различными радиусами R = y(x), площадь которых равна:

Следовательно, объем полученного тела можно найти по формуле

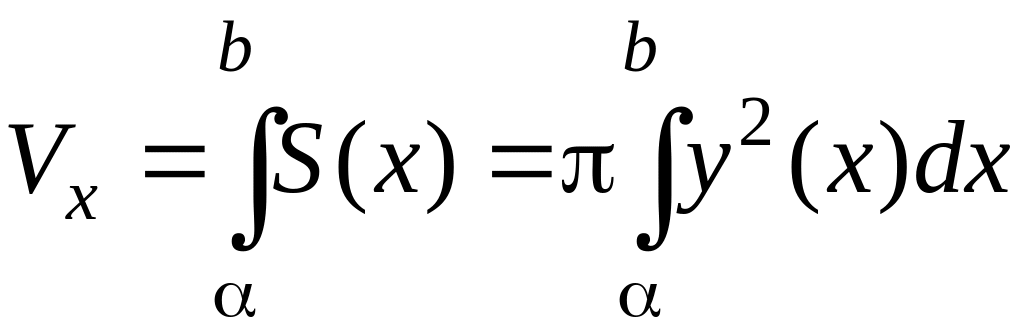
П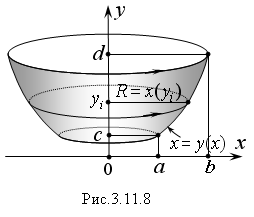 ри вращении линии, ограничивающей криволинейную трапецию, вокруг оси Oy (Рис. 3.11.8) объем полученного тела равен:

где x(y) – уравнение вращающейся линии решенное относительно переменной x.

Пример 7. Найти объем тела, полученного при вращении эллипса относительно осей Ox и Oy.

Р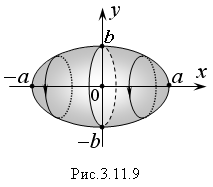 ешение. График эллипса 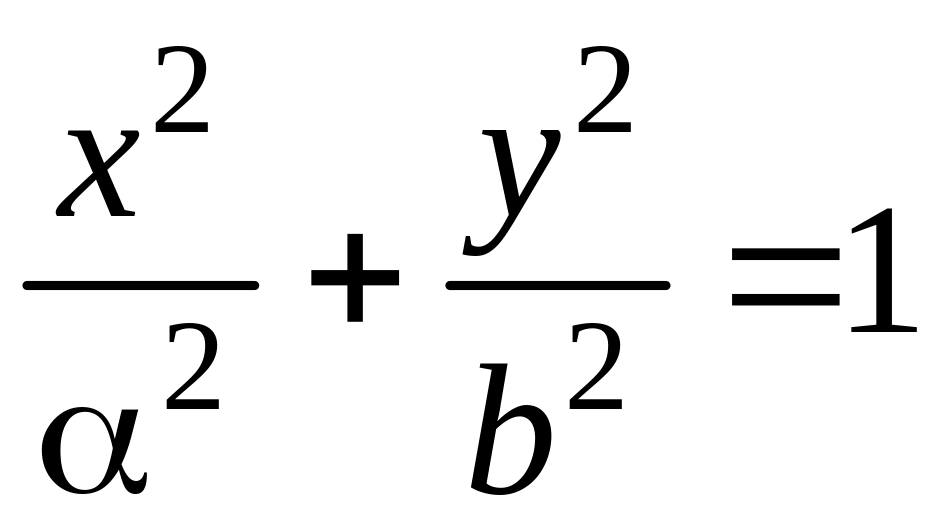изображен на рисунке 3.11.9.

Координаты его крайних точек по оси Oх: x₁ = –α, x₂ = α, по оси Oy: y₁ = –b, y₂ = b.

Объем тела, образованного вращением эллипса относительно оси Oх, найдем по формуле:

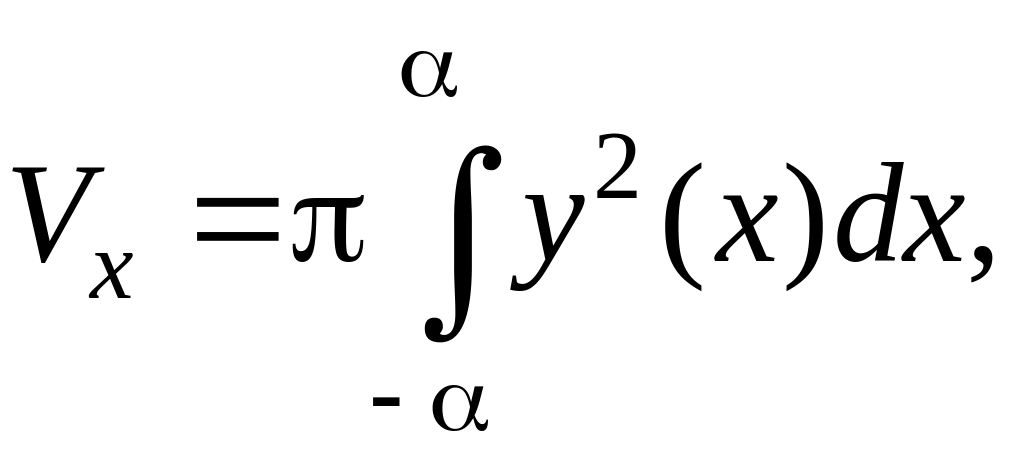где

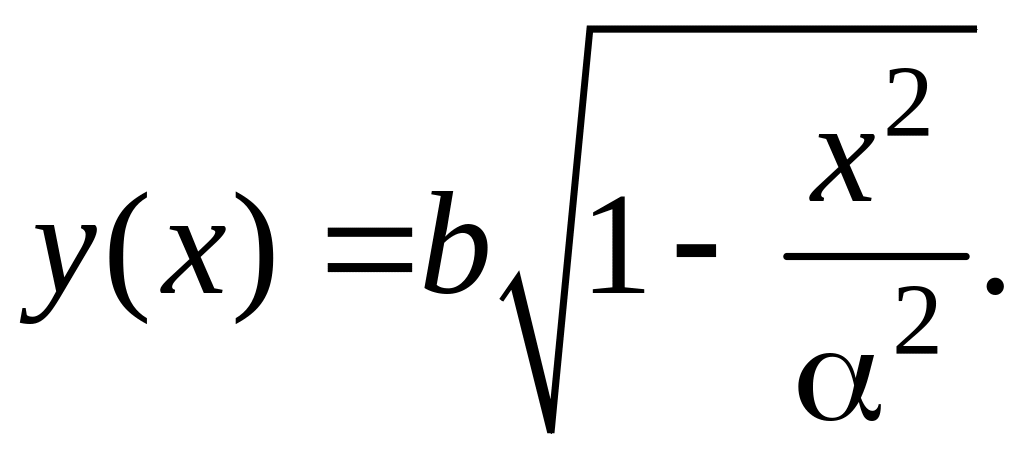
С учетом симметрии

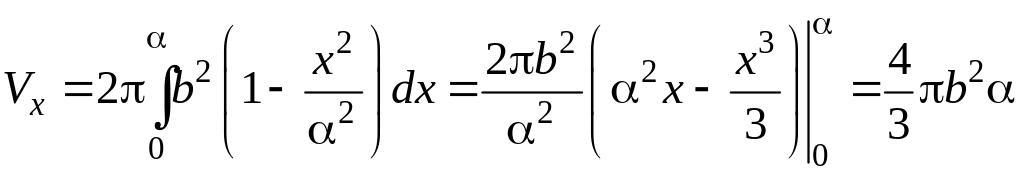
Аналогично, вычислим объем Vy

где

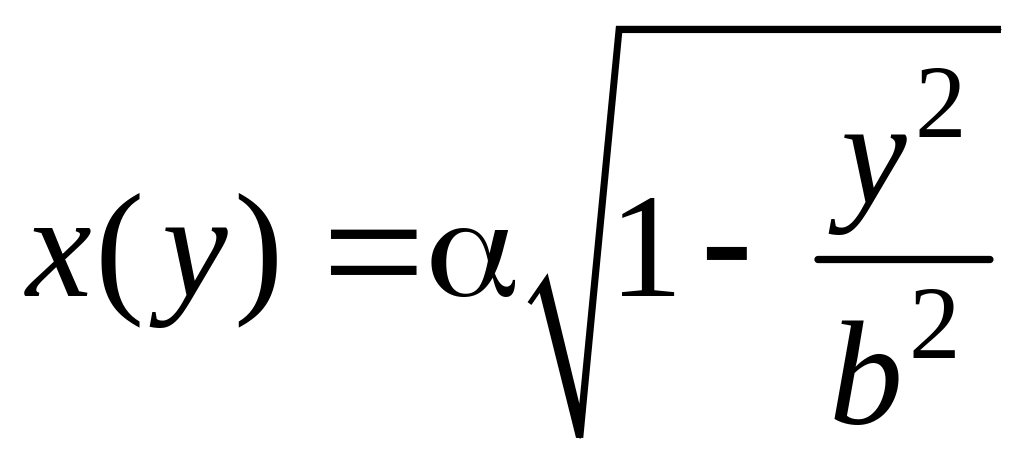
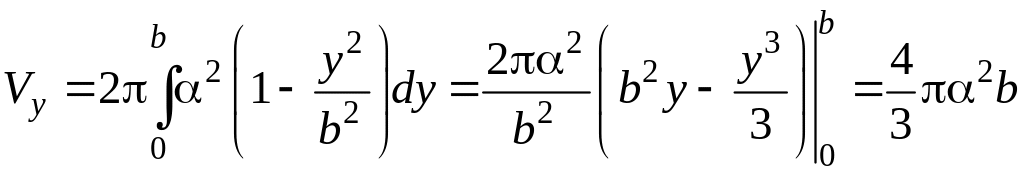
Если α = b, то тела вращения относительно осей Oх и Oy становятся шаром, объем которого равен .

Р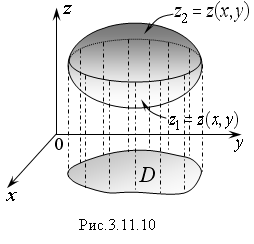 ассмотрим теперь общий случай вычисления объемов тел с помощью кратныx интегралов.

Пусть тело произвольной формы ограничено двумя поверхностями, уравнения которых известны: Проекцией данного тела на плоскость xOy является область D (Рис. 3.11.10). Двойной интеграл по области D геометрически равен объему цилиндра, построенного на этой области и ограниченного сверху графиком подынтегральной функции. Поэтому объем тела, изображенного на рисунке 3.11.10, можно представить как разность объемов двух цилиндрических тел, или как разность двух двойных интегралов:

В самом общем случае объем тел произвольной формы находят с помощью тройного интеграла, в котором подынтегральная функция равна единице

Легко заметить, что предыдущая формула является следствием последней, в самом деле:

Пример 8. Найти объем, ограниченный поверхностями:

z = 0, z + x = 6

Р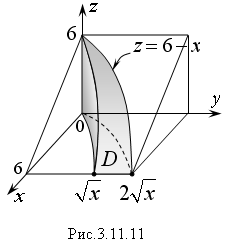 ешение. Тело ограничено двумя цилиндрическими поверхностями с образующими, параллельными оси Oz, и двумя плоскостями z = 0, z = 6 – x. Искомый объем равен объему цилиндрического тела, построенного на области D и ограниченного сверху плоскостью z = 6 – x (Рис. 3.11.11). Найдем его с помощью двойного интеграла

Переменная x внутри области D изменяется от 0 до 6, а переменная y от ее значений на линии до значений на линии . Перейдем к двукратному интегрированию:

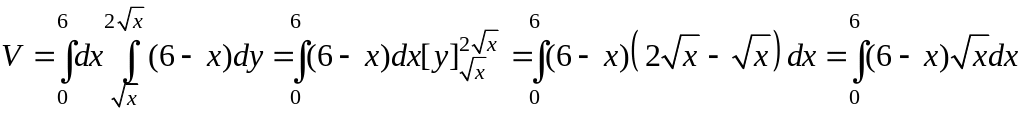
Вычисляя последний интеграл, получим

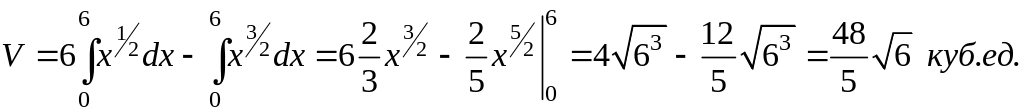
Для сравнения найдем этот же объем с помощью тройного интеграла

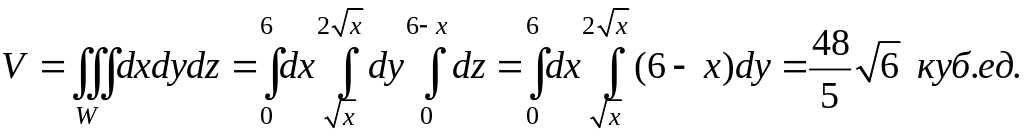
После подстановки пределов для переменной z мы приходим к такому же двойному интегралу.