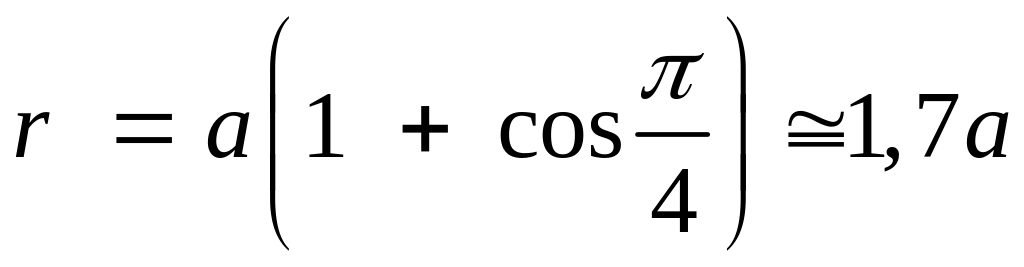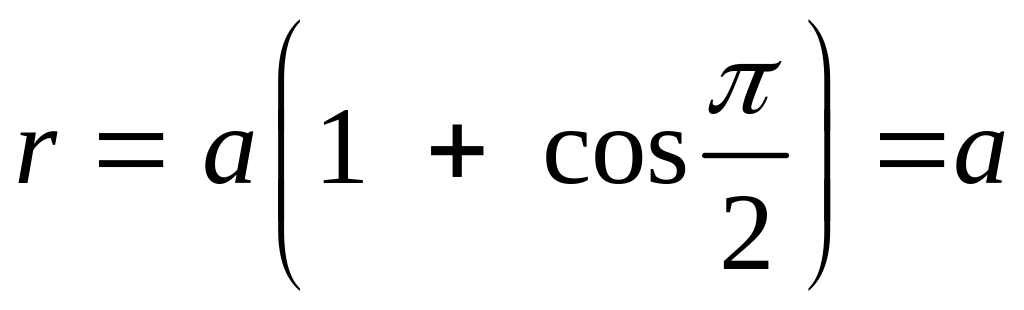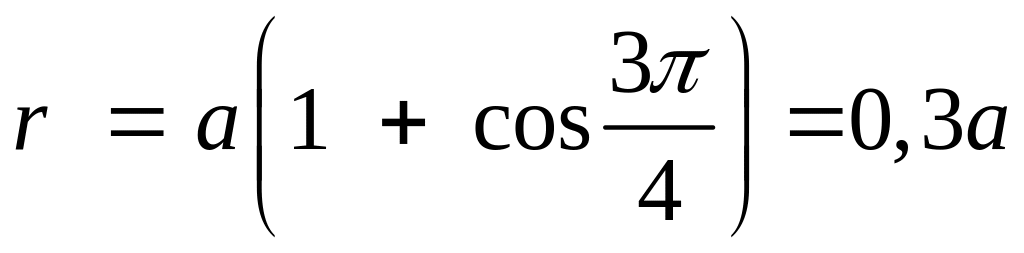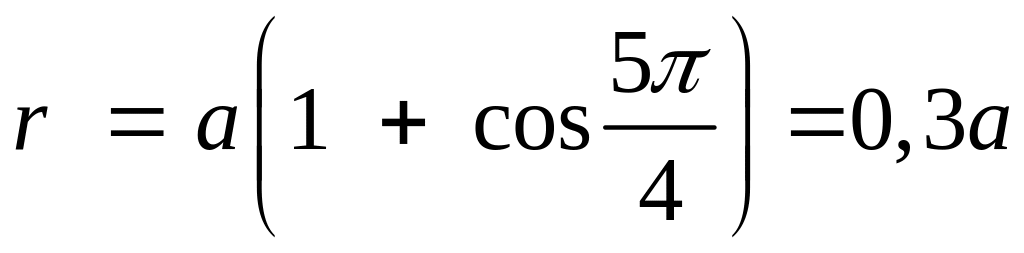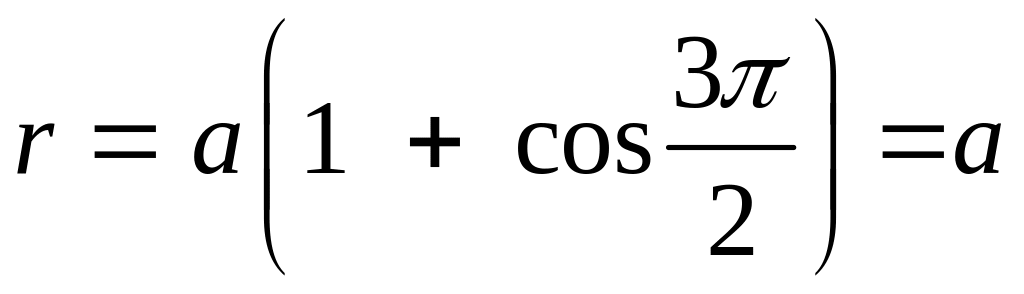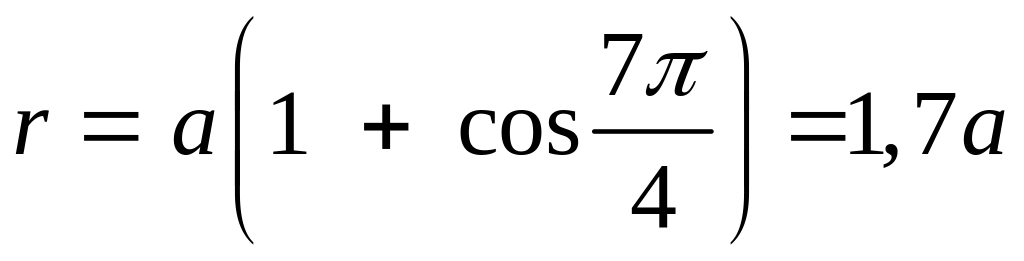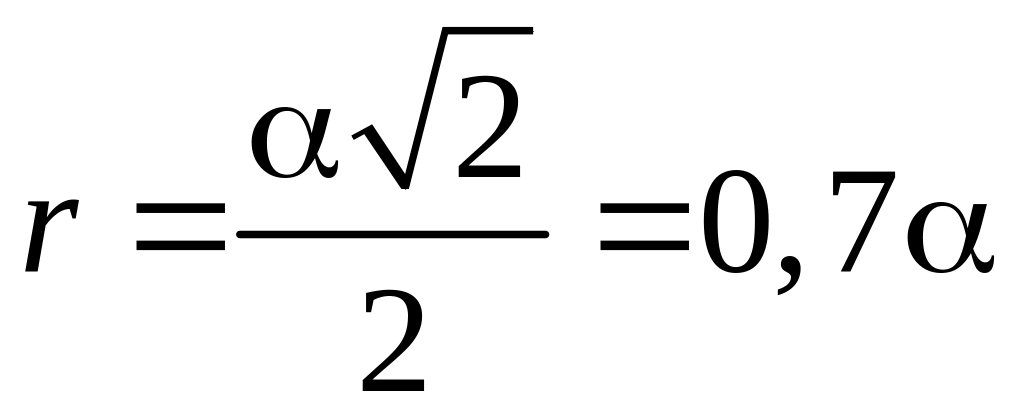Лекция 3.9. Вычисление криволинейного, двойного и тройного интегралов путем сведения к линейному

3.9.1 Уравнения линий в полярной системе координат

П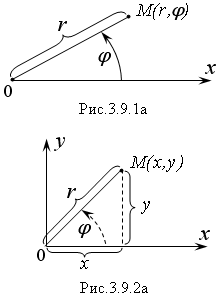 олярная система координат состоит: из начала отсчета или полюса (точка О) (Рис.3.9.1а) и полярной оси Ох. Возьмем произвольную точку на плоскости – М. Расстояние от этой точки до полюса О называют полярным радиусом, обозначают – r. Угол, на который нужно повернуть полярную ось до совпадения с полярным радиусом, называют полярным углом, обозначают – φ. Таким образом, положение любой точки на плоскости в полярной системе, так же как и в декартовой, однозначно задается двумя числами: расстоянием до полюса – r и полярным углом – φ.

Совместим начало отсчета декартовой и полярной систем и найдем координаты одной и той же точки М в этих системах (Рис.3.9.2а). Тогда, декартовы координаты точки М будут связаны с ее полярными координатами соотношениями:

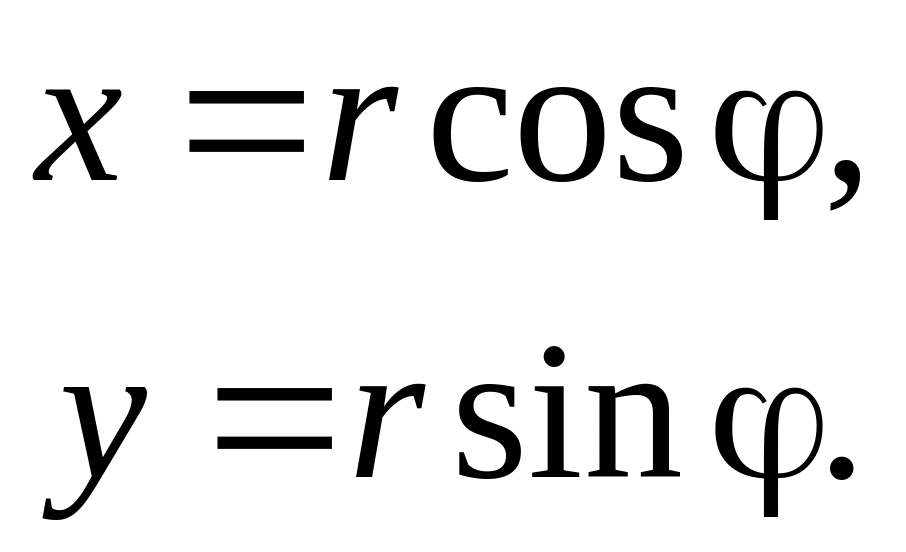
Из последних равенств легко получить выражения через х и y для полярных координат r и φ точки М:

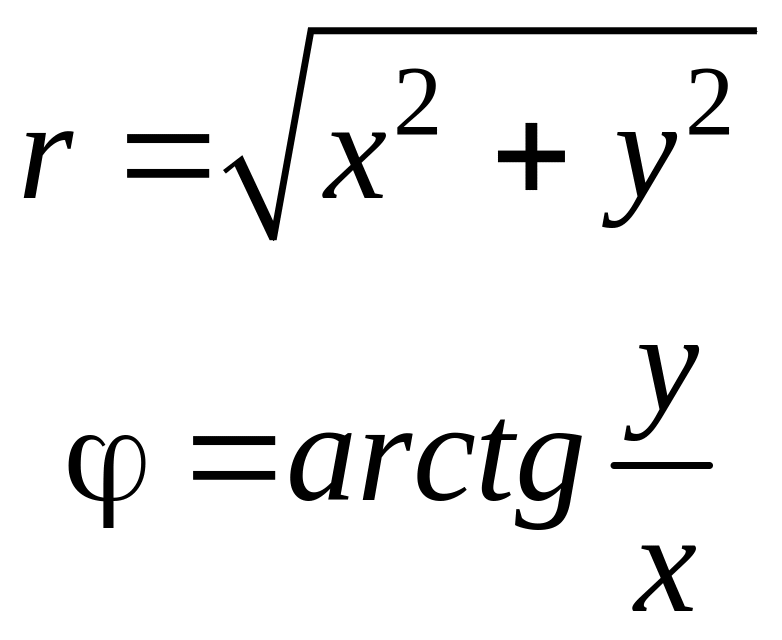
Уравнение линии на плоскости в декартовой системе координат представляет собой функцию одного переменного y = f(x), которая связывает декартовы координаты точек (x,y), лежащих на этой линии.

Аналогично, уравнение линии в полярной системе отсчета должно связывать полярные координаты точек (r,φ), принадлежащих данной линии, т.е.: r = f(φ) или r = r(φ), и также является функцией одного переменного φ. Чтобы построить график линии, заданной уравнением r = r(φ), нужно для каждого значения полярного угла φ(выбранного произвольно) найти соответствующее значение r из уравнения r = r(φ), и отложить его на полярной оси, повернутой на соответствующий угол φ. Соединяя построенные таким образом точки, получают уравнение линии.

Пример 1. Построить график линии, заданной уравнением:

Решение. Будем изменять полярный угол φ в пределах от 0 до 2π с шагом . Соответствующие значения полярного радиуса r занесем в таблицу.

N
М1
М2
М3
М4
М5
М6
М7
М8
М9

С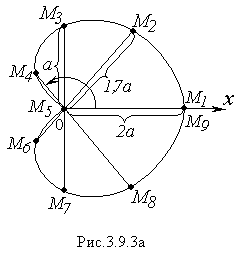 оединяя точки на плоскости с найденными полярными координатами (r,φ), получим линию (Рис.3.9.3а), которую называют кардиоидой.

В заключении скажем о координатных линиях, т.е. о линиях, на которых одна или другая координата сохраняют постоянное значение.

В декартовой системе координатные линии x = const и y = const образуют два семейства прямых, параллельных одной или другой из осей координат. В полярной системе линии r = const представляют собой семейство концентрических окружностей, а линии φ = const – семейство лучей, выходящих из полюса.

3.9.2 Вычисление криволинейного интеграла

Криволинейный интеграл по кривой L от заданной на ней функции f(p) записывают следующим образом:

(3.9.1а)

где L – конечная часть линии, определяющая область интегрирования;

dℓ - длина (мера) бесконечно малых элементов линии;

f(p) – подынтегральная функция, значения которой берутся в точках L.

Криволинейный интеграл вычисляют путем сведения его к линейному интегралу, при этом должно быть задано:

уравнение линии L, по которой ведется интегрирование,

координаты начальной и конечной точек этой линии.

Уравнение плоской кривой L можно задать различными способами (в декартовой, полярной системах координат или параметрически). Поэтому рассмотрим сведение криволинейного интеграла к линейному в каждом конкретном случае.

а. Пусть линия L – является плоской кривой и задана в декартовой системе координат уравнением y = y(x), которое представляет собой непрерывную и дифференцируемую функцию на интервале [α,b]. Тогда часть линии между точками А и В (обозначим ее L_AB) не будет иметь изломов.

В точках L_AB задана некоторая функция

(например, плотность массы или заряда), график которой схематически изображен на рисунке 3.9.4а. Эту функцию мы интегрируем, и ее не следует путать с уравнением линии y = y(x).

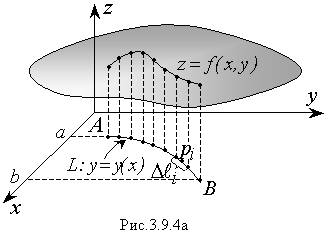
Переход от криволинейного интеграла к линейному, вывод которого мы не приводим, осуществляют следующим образом:

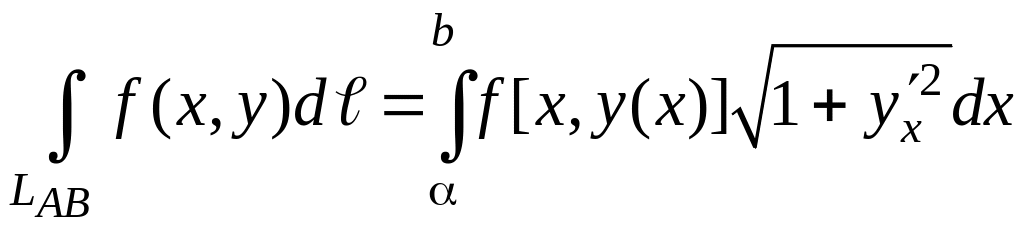(3.9.2а)

Как следует из формулы (3.9.2а), чтобы свести криволинейный интеграл по плоской кривой к линейному, нужно проделать две операции:

во-первых, у подынтегральной функции f(x,y) переменную y нужно заменить ее выражением через x из уравнения кривой y = y(x);

во-вторых, дифференциал длины dℓ следует также выразить через уравнение линии по формуле

При этом нужно помнить, что элемент длины dℓ выражается через уравнение линии L только в том случае, когда это уравнение является дифференцируемой функцией на интервале [α,b], т.е. линия L_AB гладкая и не имеет изломов.

б. А теперь рассмотрим криволинейный интеграл:

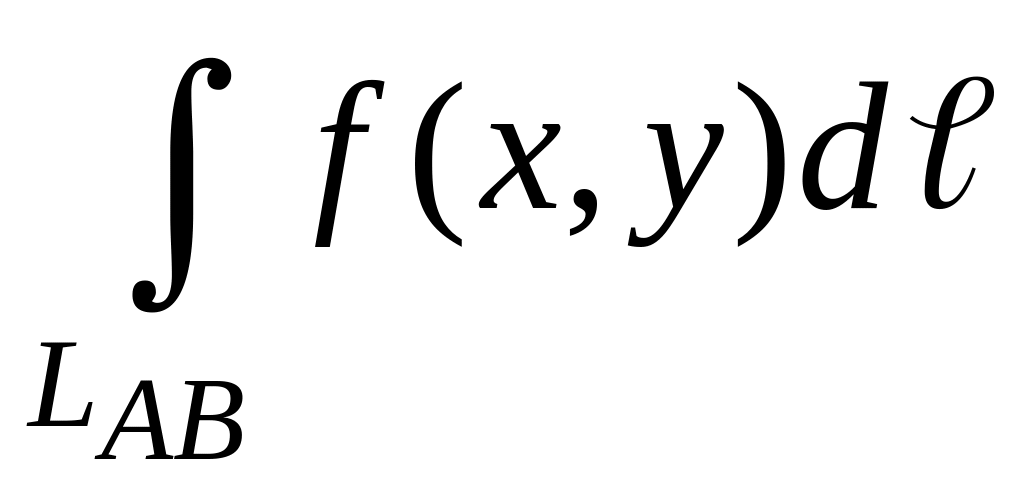
по линии L_AB, которая задана параметрически уравнениями:

x = x(t)

y = y(t).

В ее начальной точке А(x₁,y₁) – параметр принимает значения – t₁, в конечной В(x₁,y₁) – t₂. Найдем выражение для dℓ через параметрическое уравнение линии L_AB. Если учесть, что:

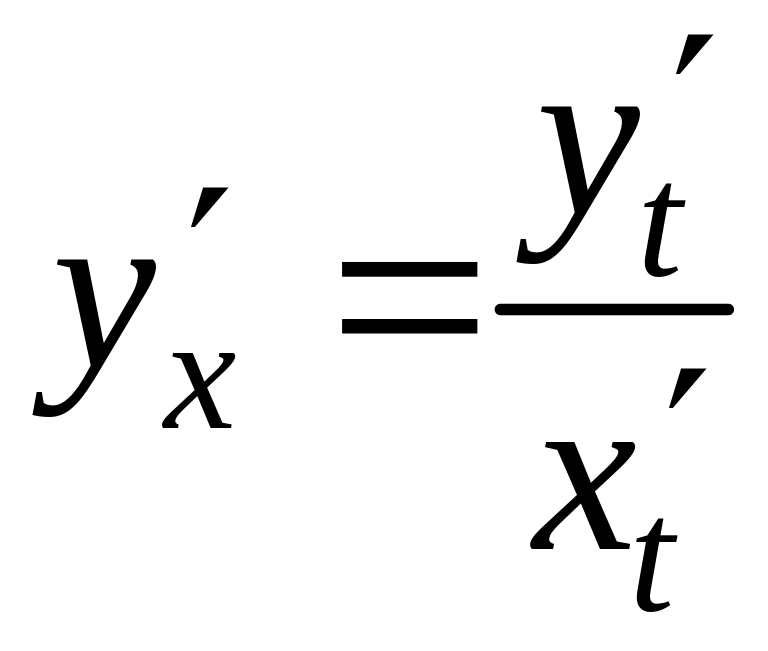и то

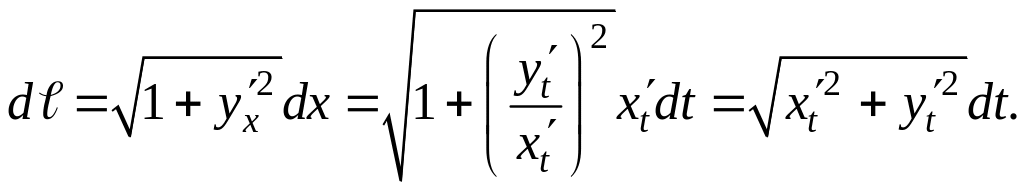
Заменим у подынтегральной функции f(x,y) переменные x и y их зависимостью от параметра t из уравнения линии x = x(t), y = y(t), а вместо дифференциала dℓ подставим найденное для него выражение через это же уравнение. В результате получим линейный интеграл от функции одного переменного t:

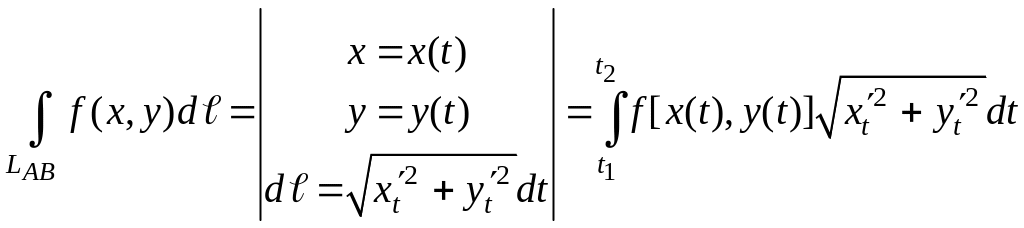(3.9.3а)

в. И наконец, пусть линия L_AB задана в полярной системе координат уравнением:

r = r(φ)

Полярные координаты начальной и конечной точек линии соответственно равны

.

Выразим дифференциал длины линии dℓ через ее уравнение r = r(φ). Полярные координаты точек, принадлежащих линии L_AB, будут связаны с их декартовыми координатами следующими отношениями:

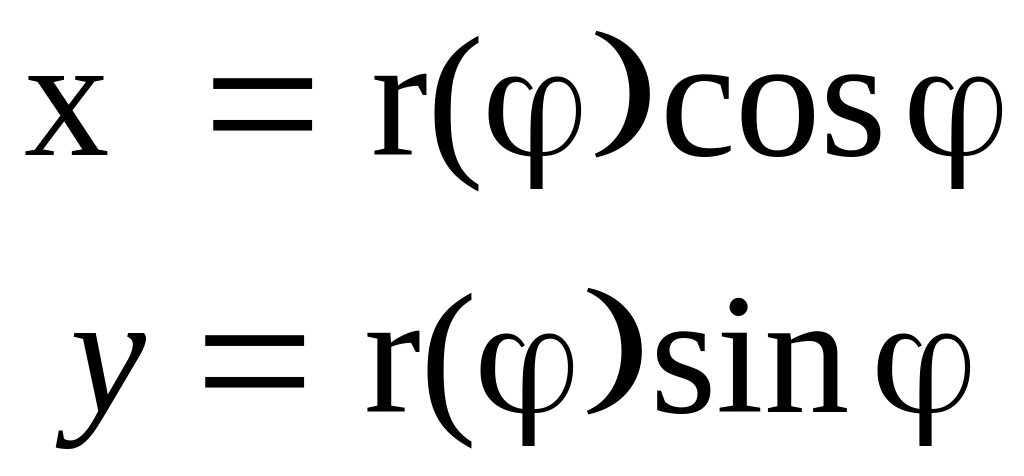(3.9.4а)

где r(φ) – полярное уравнение L_AB. Полярный угол φ можно рассматривать как параметр, а соотношение (3.9.4а) – параметрическими уравнениями линии L_AB, тогда:

(3.9.5а)

Найдем производные и :

Возьмем в квадрат обе части последних равенств и сложим:

(3.9.6а)

Подставим в выражение для dℓ (3.9.5а) вместо правую часть равенства (3.9.6а), получим:

(3.9.7а)

Чтобы перейти к линейному интегралу, нужно заменить дифференциал длины dℓ через уравнение линии r = r(φ) по формуле (3.9.7а), а переменные y и x у функции f(x,y) – их зависимостью от φ из соотношений (3.9.4а):

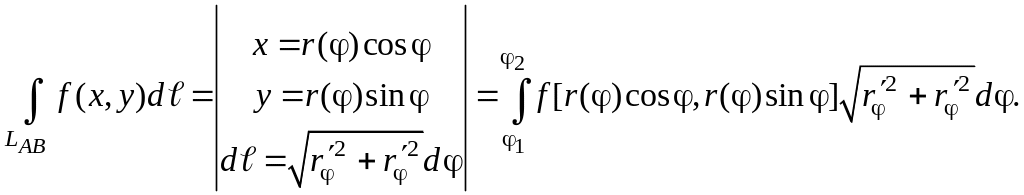
Сведение криволинейного интеграла к линейному во всех трех случаях по идее очень близко к замене переменной в линейном интеграле. Однако, нужно иметь в виду одно отличие. После замены переменной в линейном интеграле может оказаться, что нижний предел больше верхнего. При вычислении же криволинейного интеграла всегда нижний предел должен быть меньше верхнего. Это обусловлено тем, что элемент длины dℓ не может быть отрицательным, поэтому в формулах

dx, dt, dφ тоже всегда больше нуля, а это значит, что при переходе от криволинейного интеграла к линейному переменная интегрирования пробегает свои значения в сторону возрастания.

П ример 2. Найти массу одной четверти окружности x² + y² = α², расположенной в первом квадранте, если плотность массы задана функцией ρ = xy.

Решение. Обозначим массу кривой – М. Так как кривая неоднородна, ее масса равна криволинейному интегралу:

по четверти окружности (Рис.3.9.5а). Выразим дифференциал длины окружности через ее уравнение по формуле:

где

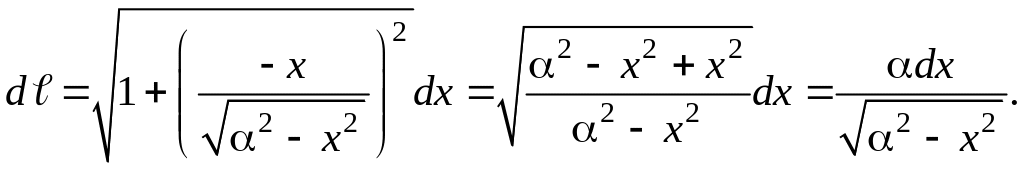
У подынтегральной функции ρ(x,y) = xy переменную y заменим ее зависимостью от x из уравнения окружности а вместо dℓ подставим найденное для него значение, получим:

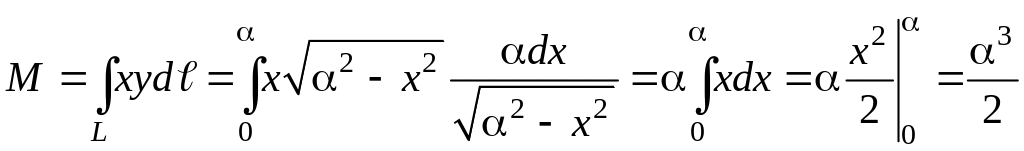
Масса четверти данной окружности зависит от ее радиуса α.

Пример 3. Вычислить криволинейный интеграл где L первая арка циклоиды:

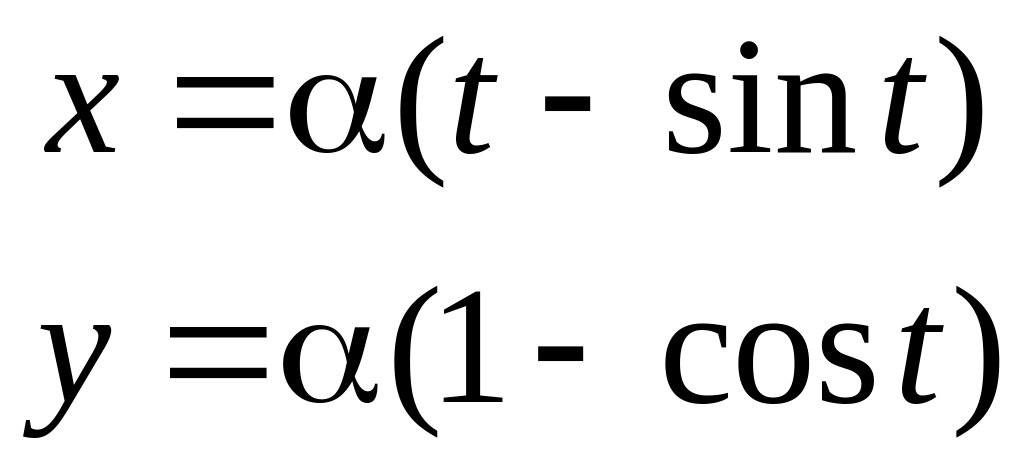
Решение. Уравнение кривой L задано параметрически. Найдем значение параметра t в начальной и конечной точках первой арки циклоиды. Для этого построим ее график. Будем изменять параметр t через интервал

Соответствующие значения координат x и y занесем в таблицу:

График первой арки циклоиды (Рис.3.9.6а) получается при изменении параметра t от 0 до 2π.

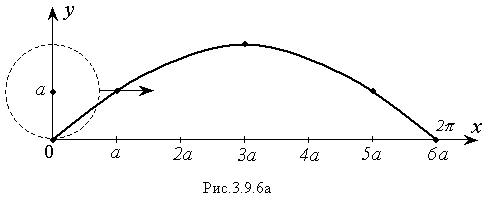
Циклоида представляет собой траекторию точки окружности, катящейся без скольжения по оси Ох.

Дифференциал длины линии, заданной параметрически, выражается через ее уравнение по формуле Найдем его для данной кривой:

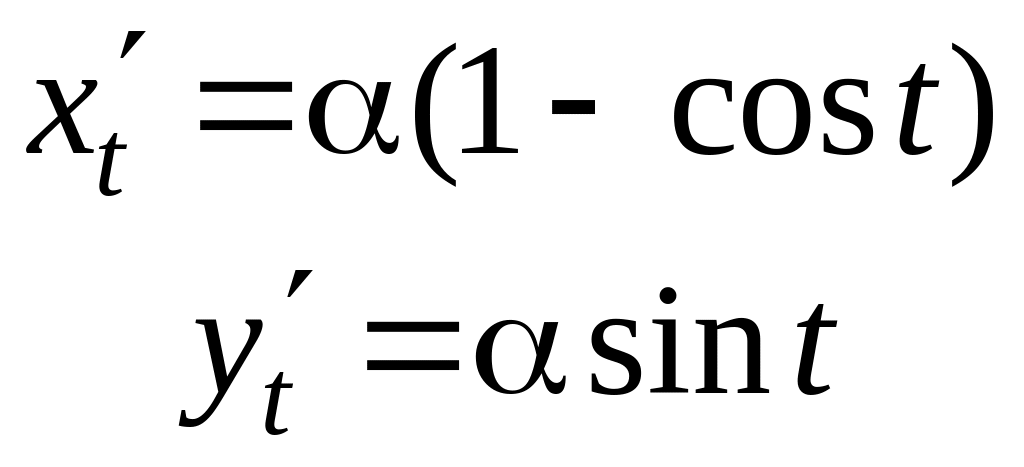
Подставляя производные в выражение для dℓ, получим

Заменим у подынтегральной функции переменную y ее зависимостью от t из уравнения циклоиды и подставим найденное значение dℓ:

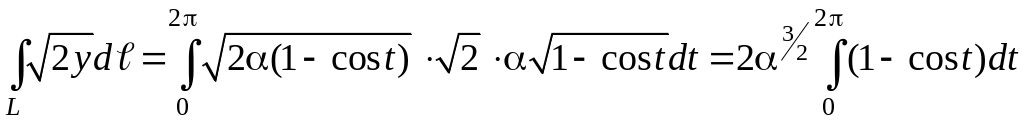
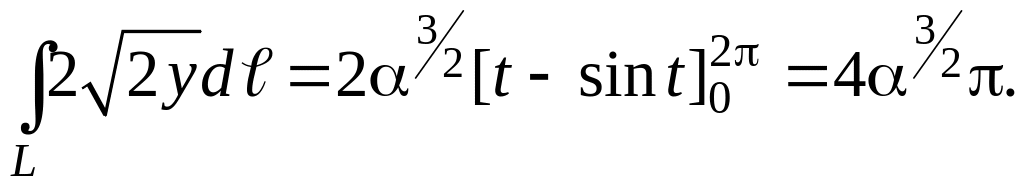
Окончательный результат получен по формуле Ньютона-Лейбница.

Пример 4. Вычислить криволинейный интеграл

где L: r = α сosφ.

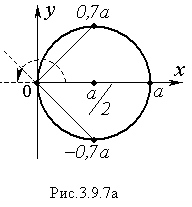
Решение. Найдем пределы изменения полярного угла φ. Построим график линии L.

Уравнение r = αcosφ задает окружность с радиусом и центром, смещенным от полюса по полярной оси вправо на (Рис.3.9.7а). При этом полярный угол φ изменяется от 0до π.

Перейдем от криволинейного интеграла к линейному по формуле:

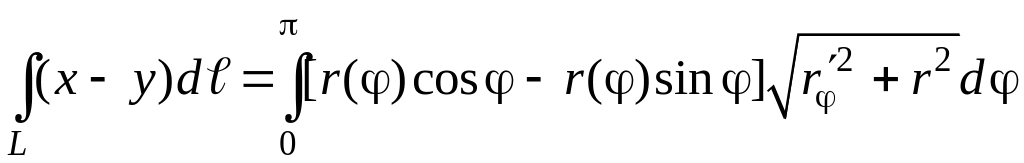
Подставляя вместо r(φ) уравнение линии и производную от него, получим:

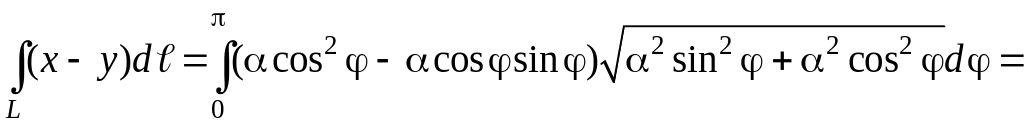
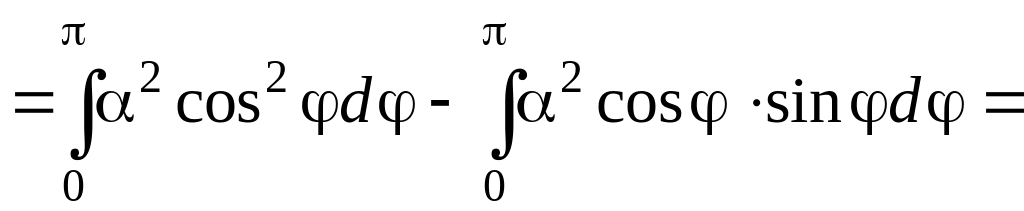
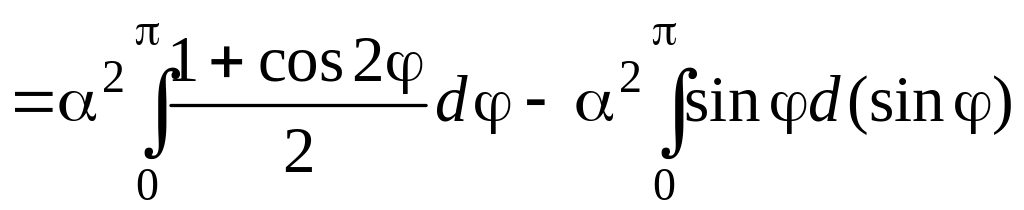
Криволинейный интеграл будет равен:

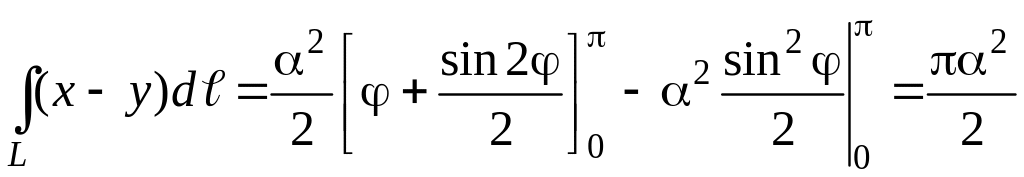
В разобранных примерах мы пытались показать, как осуществляют переход от криволинейного интеграла по длине дуги к линейному в случаях различного задания уравнения линии L, по которой ведется интегрирование. Помимо криволинейных интегралов по длине дуги рассматривают криволинейные интегралы по координатам (второго рода). Эти интегралы подробно разобраны в разделе «Теория поля». Поэтому здесь на них мы останавливаться не будем.