3.8.2. Формула трапеций

Вычислим площадь криволинейной трапеции, ограниченной сверху графиком подынтегральной, другим способом. По-прежнему разобьем интервал интегрирования на n-равных частей с длинами:

.

В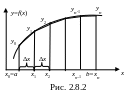 место прямоугольников на всех частичных интервалах построим трапеции с высотами, равными Δх (Рис.3.8.2), т.е. подынтегральную функцию на частичных интервалах заменим прямыми, проходящими через её значения на границах (многочленами первой степени). Тогда величина интеграла будет приближенно равна сумме площадей построенных прямолинейных трапеций:

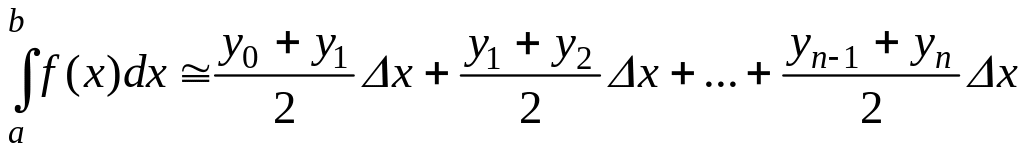или

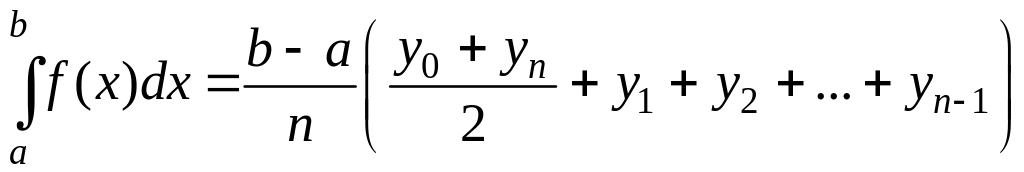(3.8.4)

Полученную формулу (3.8.4) называют формулой трапеции. Абсолютная ошибка, которая получается при вычислении интеграла по этой формуле, не превосходит величины:

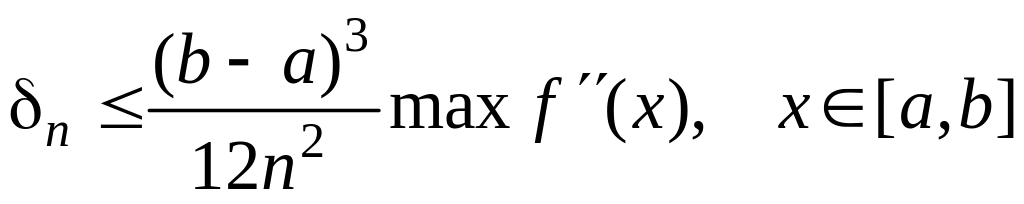(3.8.5)

Однако, она в два раза больше по сравнению с методом средних прямоугольников. В обоих случаях, чем больше n – тем меньше ошибка.

На практике обычно трудно определить mах f" (х), поэтому для оценки верхней границы погрешности пользуются другим выражением:

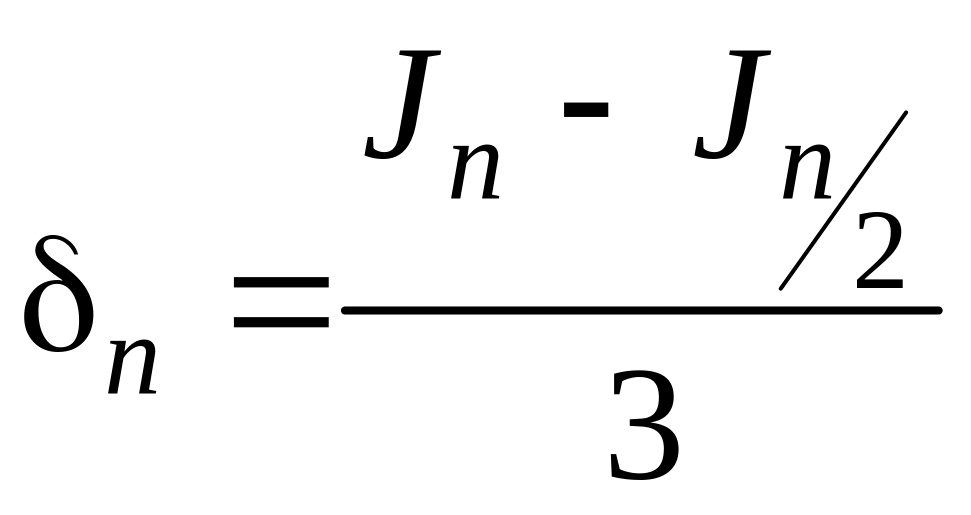(3.8.6)

Формулу (3.8.6) получают следующим образом. Уменьшим число разбиений интервала [а, b] в два раза: n/2 и найдем, во сколько раз возрастет верхняя граница ошибки

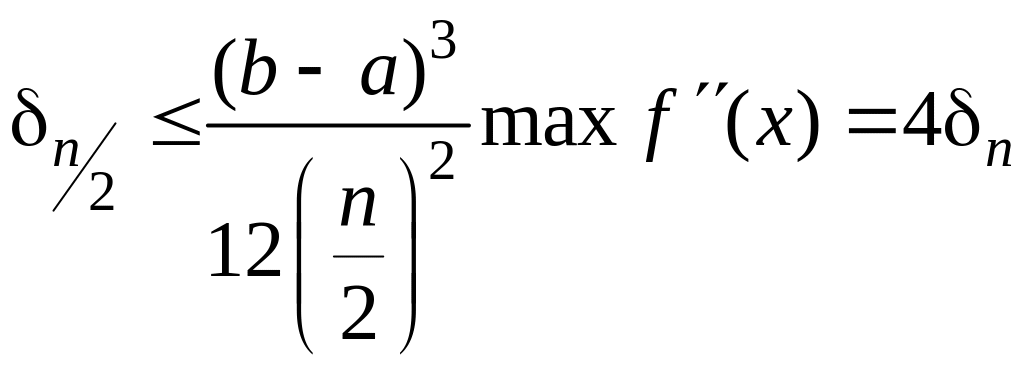
Точное значение линейного интеграла можно записать двумя способами

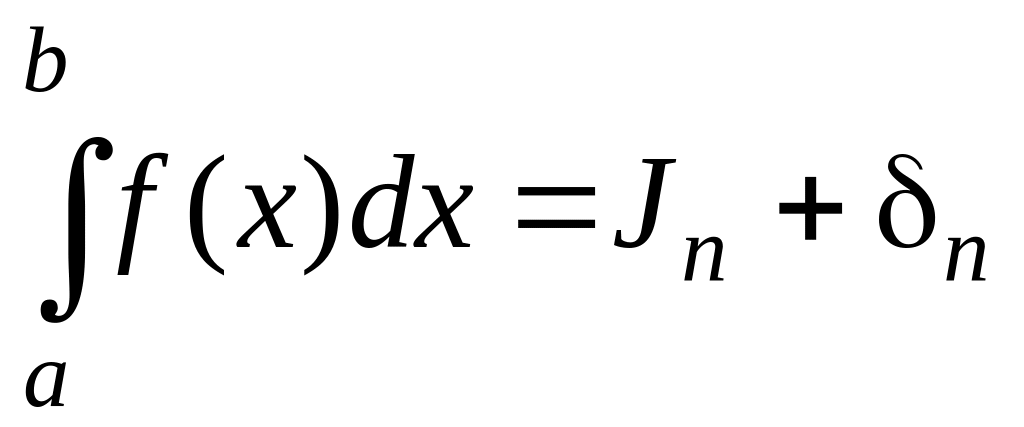(3.8.7)

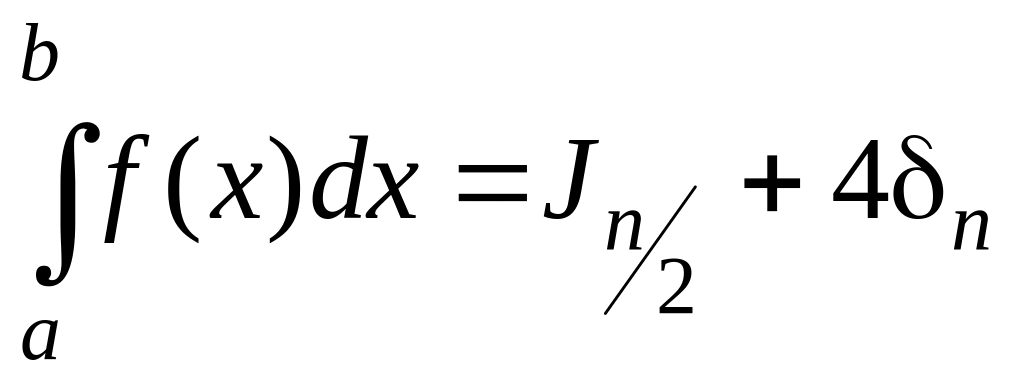(3.8.8)

где J_n – приближенное значение интеграла, полученное при разбиении интервала [а, b] на n частей J_n/2 – приближенное значение интеграла при разбиении на . Вычитая соответствующие части равенств (3.8.7) и (3.8.8), получим: 0= J_n – J_n/2 – 3δ_n.

Откуда следует, что

.

3.8.3. Формула парабол (формула Симпсона)

По-прежнему, требуется вычислить интеграл , значение которого равно площади криволинейной трапеции.

Разобьем интервал [а, b] на чётное число равных частей – n:

.

у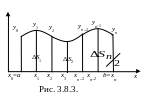

На сдвоенных частичных интервалах: х₂ – х₀, х₄ – х₂, …, х_n – х_n-2 длиною 2h участки графика подынтегральной функции заменим параболами у = Ах² + Вх + С или многочленом второй степени.

Значение интеграла приближенно будет равно сумме площадей частичных параболических трапеций (Рис. 3.8.3):

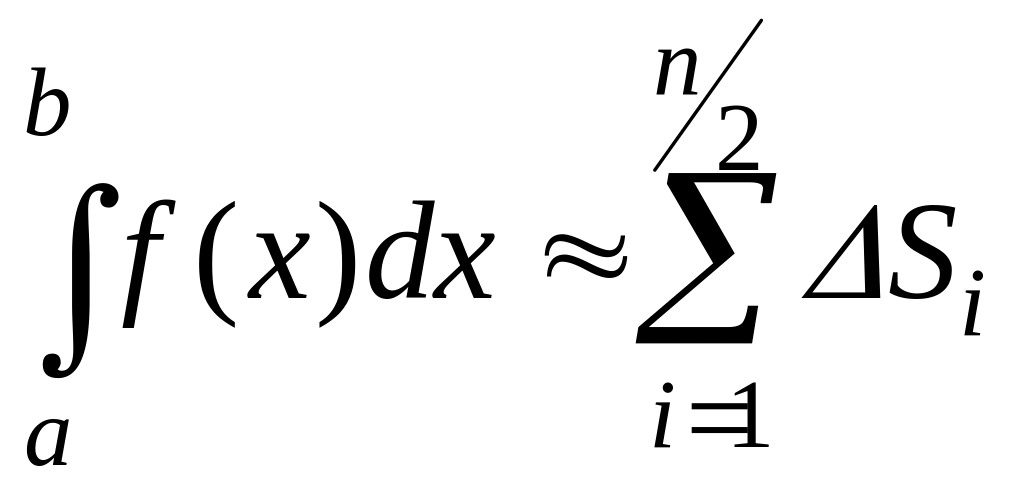(3.8.9)

Найдем площадь первой параболической трапеции ΔS₁ . Так как ΔS₁ ограничена сверху параболой у = Ах² + Вх + С (Рис. 4), то её площадь равна линейному интегралу:

.

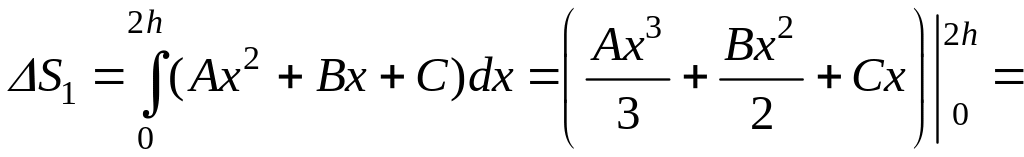
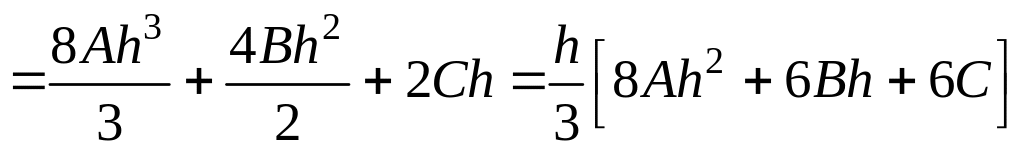О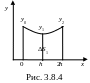 рдинаты подынтегральной функции у = f(х), которую мы заменили параболой, в точках х = 0, х = h, х = 2h равны у₀, у₁, у₂ (Рис. 3.8.4). Выразим коэффициенты А, В, С параболы через ординаты функции у₀, у₁, у₂:

у = Ах² + Вх + С = f(х)

при х = 0 у₀ = С

при х = h у₁ = Аh² + Вh + С (3.8.10)

при х = 2h у₂ = 4Аh² + 2Вh + С

с учетом равенств (3.8.10) перепишем найденное значение ΔS₁ в виде:

.

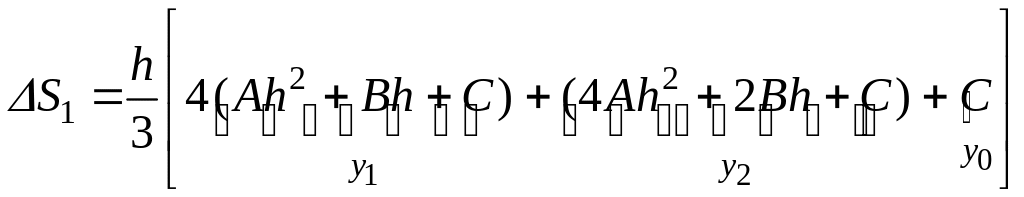Итак, площадь первой параболической трапеции равна:

.

Аналогично выразятся площади ΔS₂, ΔS₃, …, ΔS_n/2 последующих параболических трапеций

………………………….

.

Сложив почленно все эти равенства найдем приближенное значение искомого интеграла:

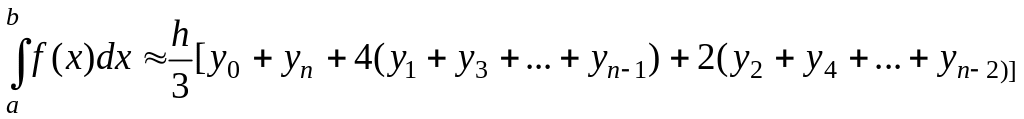(3.8.11)

Формулу (3.8.11) называют формулой парабол или формулой Симпсона. Верхняя граница погрешности при вычислениях интеграла по этой формуле равна

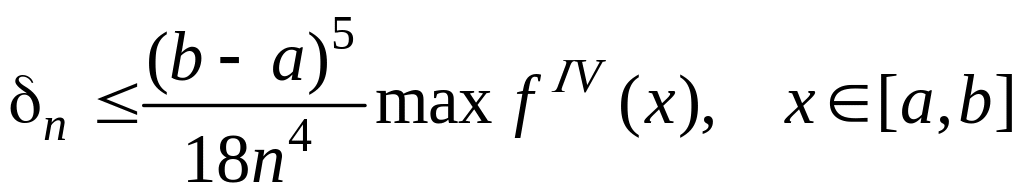(3.8.12)

Погрешность имеет четвертый порядок малости. Формула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. На практике в случае формулы Симпсона для δ_n. Пользуется таким равенством:

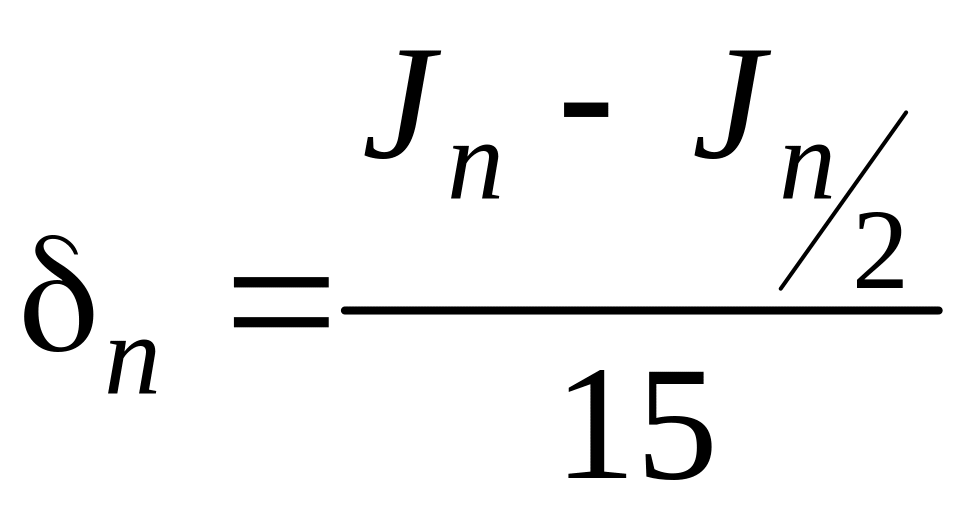(3.8.13)

Его получают аналогично равенству (3.8.6). При уменьшении числа разбиений интервала [а, b] в два раза, верхняя граница ошибки возрастает в 16 раз:

,

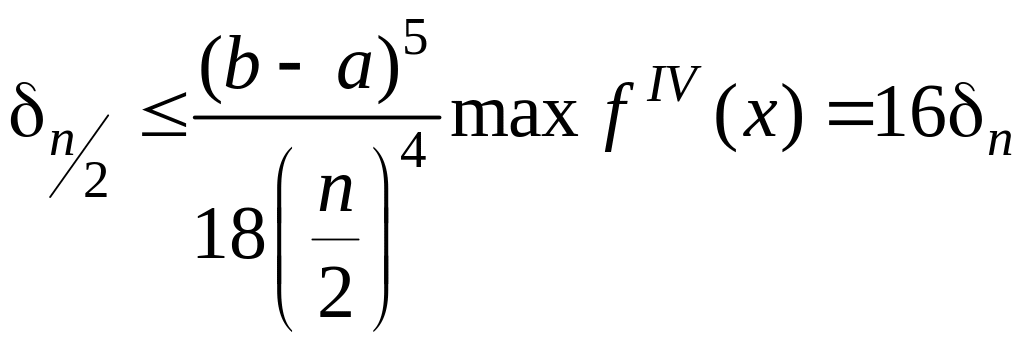поэтому 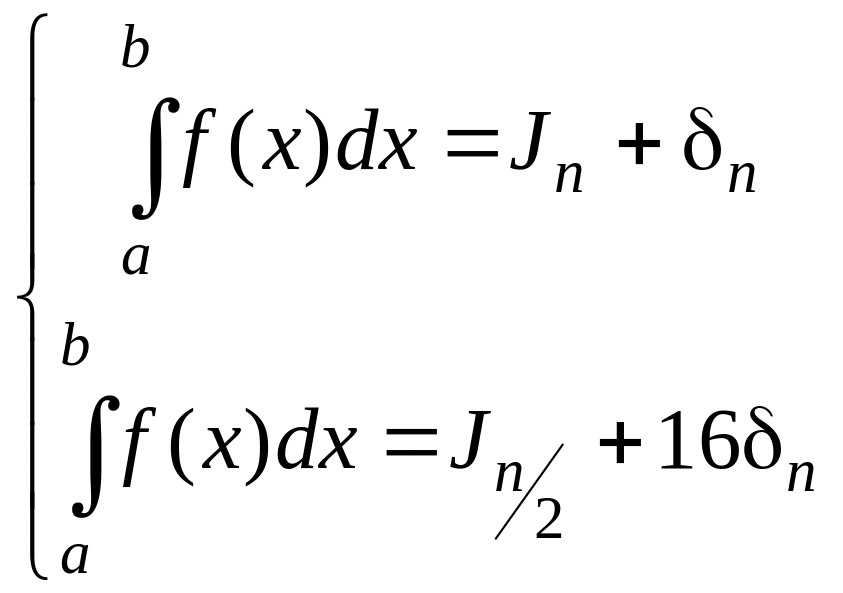; отсюда .

Пример. Вычислишь по формуле Ньютона-Лейбница и приближенно линейный интеграл: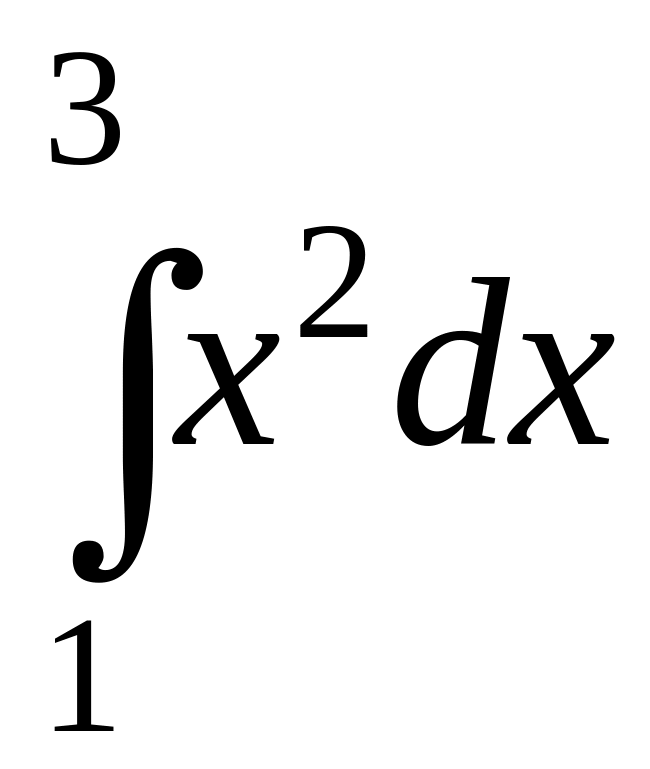 полученные результаты сравнить

1. Найдем точное значение данного интеграла по формуле Ньютона-Лейбница:

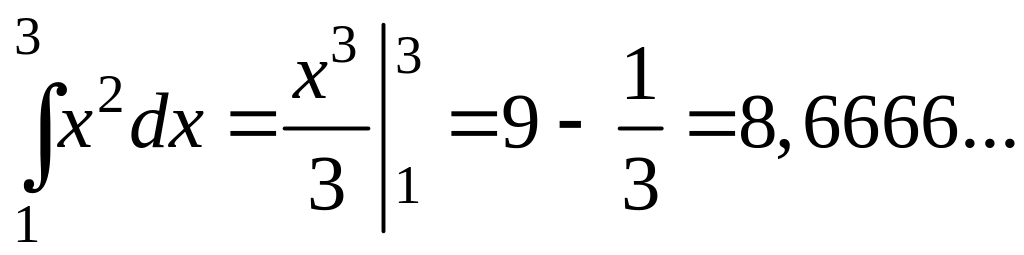
2. Построим график подынтегральной функции. Рис.3.8.5.

Разобьем интервал b – а = 3–1=2 на десять частей, т.е. n = 10

h = 0,2

Вычислим значения подынтегральной функции в точках: х₀ = 1; х₁= 1,2; х₂ = 1,4 и т.д., а также в срединах частичных интервалов. Результаты занесем в таблицу.

№	хi	у = х2	№	хi	у = х2	№
х0	1	у0 = 1	х0	1	1
х1	1,2	у1 = 1,44					1,1	=1,21
х2	1,4	у2 = 1,96	х1	1,4	1,96		1,3	= 1,69
х3	1,6	у3 = 2,56					1,5	= 2,25
х4	1,8	у4 = 3,24	х2	1,8	3,24		1,7	= 2,89
х5	2	у5 = 4					1,9	= 3,61
х6	2,2	у6 = 4,84	х3	2,2	4,84		2,1	= 4,41
х7	2,4	у7 = 5,76					2,3	= 5,29
х8	2,6	у8 = 6,76	х4	2,6	6,76		2,5	= 6,25
х9	2,8	у9 = 7,84					2,7	= 7,29
х10	3	у10 = 9	х5	3	9		2,9	= 8,41
=39,4; = 47,4								=43,3

По формуле левых прямоугольников (с недостатком) находим

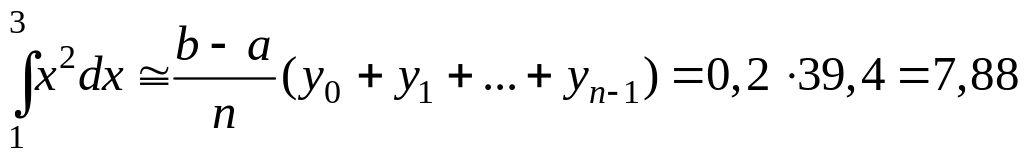
По формуле правых прямоугольников (с избытком) получим

.

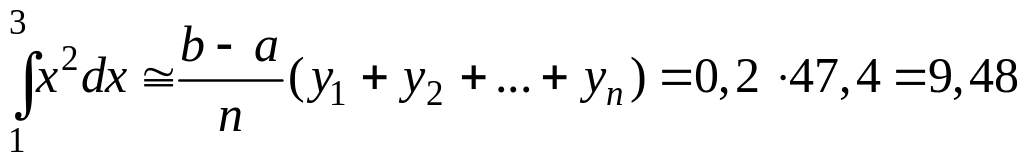Результаты сильно отличаются от истинного значения, т.е. вычисления проведены с большой погрешностью. Найдем приближенное значение данного интеграла по формуле средних прямоугольников

.

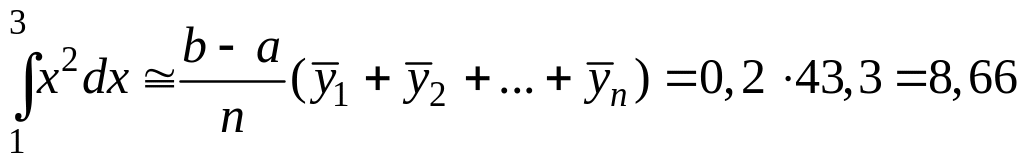Результат весьма близкий к истинному.

Для сравнения вычислим приближенное значение данного интеграла по формулам трапеций и Симпсона.

По формуле трапеций для n = 10 с шагом h = 0,2 находим

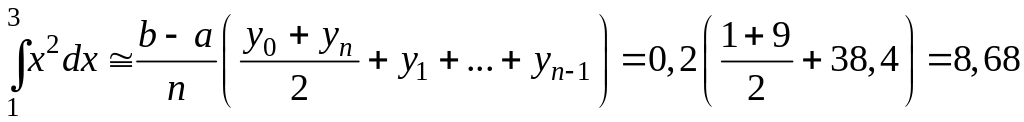
По формуле трапеций для с шагом h = 0,4 получим

.

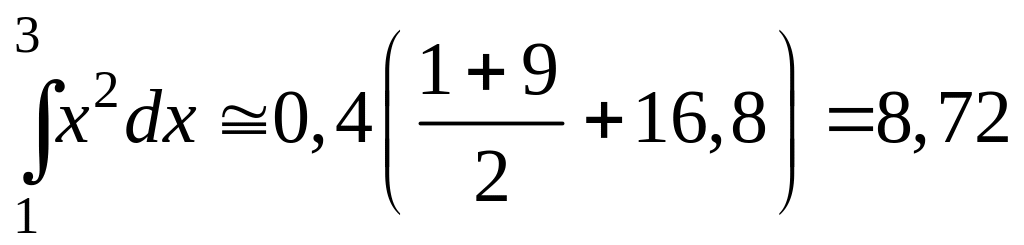Верхняя граница абсолютной ошибки равна

И, наконец, по формуле Симпсона для n = 10; h = 0,2

.

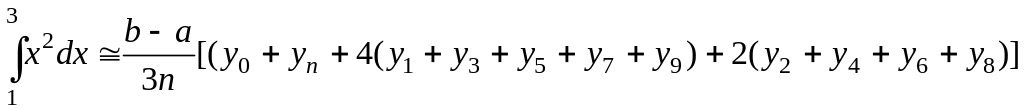
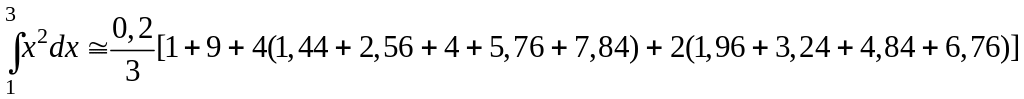
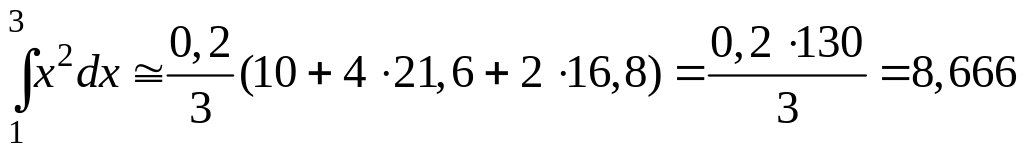Как и следовало ожидать, самую высокую точность вычислений дает формула парабол (Симпсона), а затем формула средних прямоугольников.