Лекция 3.8. Приближенное вычисление определенных интегралов. Формулы прямоугольников, трапеций, симпсона. Формулы численного интегрирования. Оценка погрешности

Вычисление линейного интеграла с помощью неопределенного по формуле Ньютона-Лейбница на практике, как уже отмечалось, не всегда возможно. Во-первых, первообразная не всегда выражается через элементарные функции или через известные неэлементарные, т.е. не всегда её можно найти. Во-вторых, найденная первообразная может оказаться очень громоздкой. И наконец функция f(х), которую надо проинтегрировать, может быть задана не формулой, а , например, таблицей значений или графиком.

Во всех этих случаях линейный интеграл вычисляют приближенно с помощью численного интегрирования. Существует много различных способов и формул для приближенного вычисления линейного интеграла. Сущность большинства из них состоит в замене подынтегральной функции f(х) аппроксимирующей функцией φ(х), для которой можно легко найти первообразную, т.е.

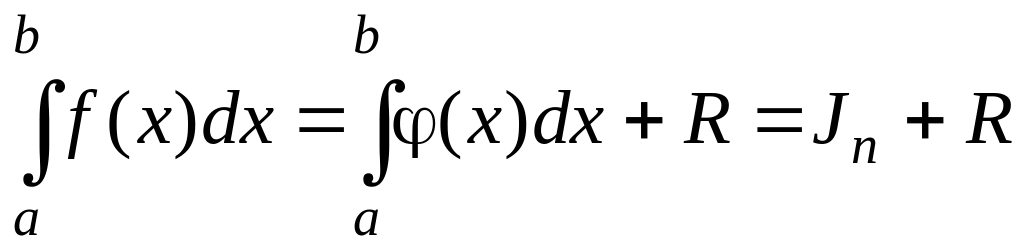
где J_n – приближенное значение интеграла,

R – погрешность вычисления.

Мы рассмотрим некоторые простейшие методы класса Ньютона-Котеса исходя из геометрического смысла линейного интеграла. В этих методах подынтегральную функцию заменяют многочленом, от степени которого зависит количество узлов, где необходимо вычислить значение функции f(х). Алгоритмы этих методов просты и легко поддаются программной реализации.

3.8.1. Формула прямоугольников

Отметим, что при выводе этой формулы подынтегральную функцию заменяют многочленом нулевой степени, т.е. числом.

Требуется вычислить: , где f(х) – непрерывна в замкнутом интервале [а, b]. Будем исходить из того, что величина интеграла равна площади криволинейной трапеции (рис.1). Вычислим эту площадь следующим образом. Разобьем интервал [а, b] на n равных частей, так что: (Рис.3.8.1).

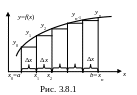
На всех частных интервалах построим прямоугольники, с высотами, равными значениям функции в начале каждого частного интервала:

у₀, у₁, …, у_n-1.

Тогда за площадь криволинейной трапеции приближенно можно принять сумму площадей построенных прямоугольников, т.е.

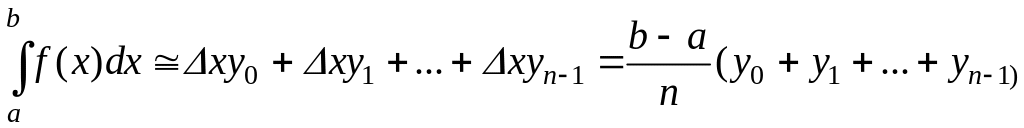(3.8.1)

Если на каждом частном интервале длиною Δх построить прямоугольники с высотами у₁, у₂, …, у_n – равными значениям функции в конце каждого частичного интервала, то величина интеграла приближенно будет равна:

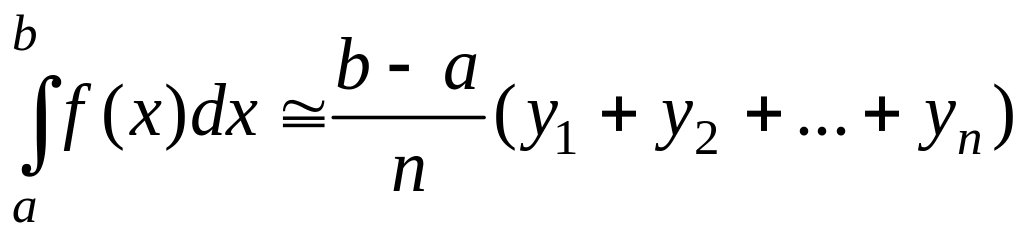(3.8.2)

Формулы (3.8.1) и (3.8.2) называют формулами левых и правых прямоугольников. В случае возрастающей функции, как показано на рисунке 3.8.1, формула (3.8.1) дает значение интеграла с недостатком (нижняя сумма Дарбу), а формула (3.8.2) с избытком.

Обе формулы имеют сравнительно большую погрешность (первого порядка малости). Так для левых прямоугольников главный член погрешности на частичном интервале равен

.

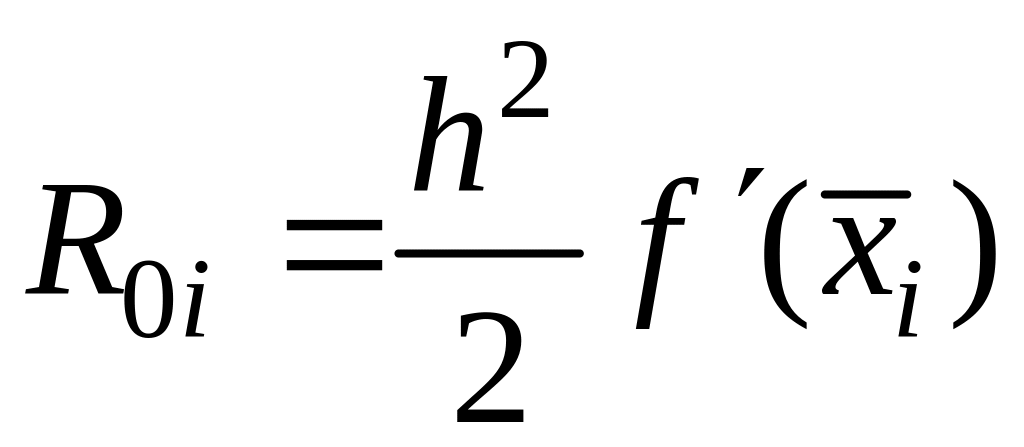Суммирование по всему интервалу [а, b] дает общую ошибку

.

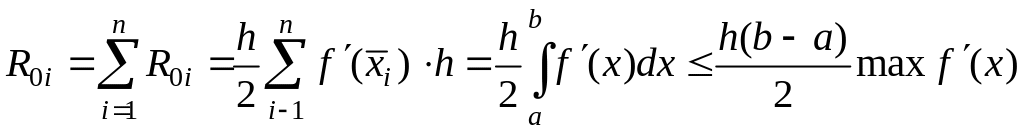Если учесть, что , то верхнюю границу абсолютной ошибки можно записать так

.

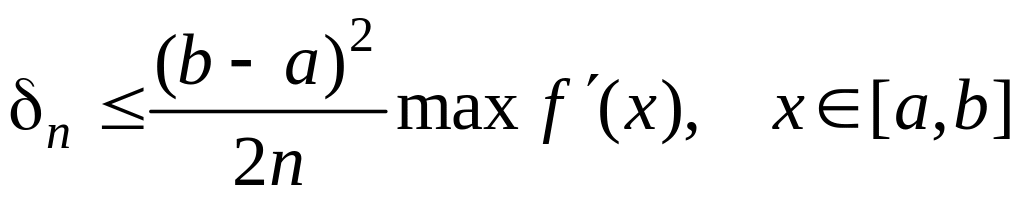При уменьшении в два раза числа разбиений интервала [а, b] абсолютная ошибка возрастает также в два раза.

По сравнению с формулами (3.8.1) и (3.8.2) более точным является метод средних прямоугольников, т.е. когда значения функции f(х) вычисляют в срединах каждого частного интервала:

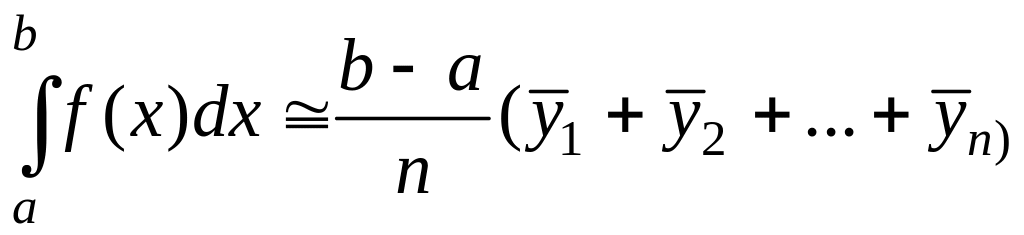(3.8.3)

При этом верхняя граница абсолютной ошибки равна

.

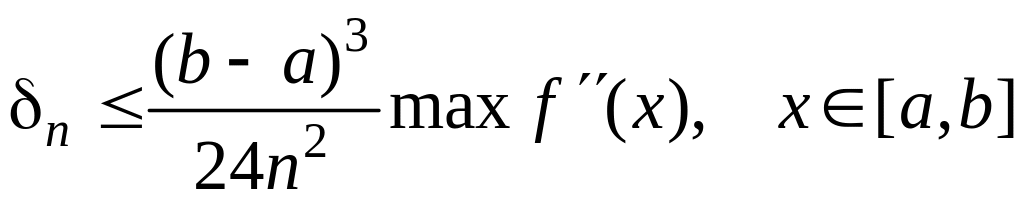Если число точек (узлов) увеличить в два раза, точность формулы (3.8.3) улучшится в четыре раза. В самом деле

.

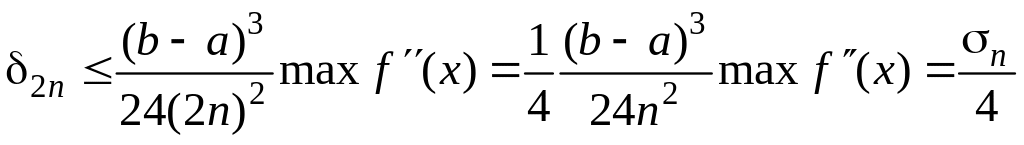Однако, если подынтегральная функция f(х) определяется из эксперимента в дискретном наборе узлов, то метод средних прямоугольников применить нельзя из-за отсутствия значений f(х) в средних точках . В этом случае для интегрирования используют другие методы Ньютона-Котеса.