Лекция 3.7. Линейный интеграл, способы вычисления. Формула ньютона–лейбница. Интегрирование по частям и замена переменных. Несобственные интегралы первого и второго рода. Признаки сходимости

Определенные интегралы всех типов вычисляют путем сведения их к линейному вида . В силу этого линейный интеграл занимает одно из центральных мест. Непосредственное вычисление этого интеграла, как предела интегральной суммы, чрезвычайно громоздкая задача. В некоторых частных случаях линейный интеграл удается найти значительно проще через неопределенный. Попробуем выяснить связь между этими интегралами.

3.7.1. Производная от линейного интеграла по переменному верхнему пределу

Пусть дана функция y=f(x), непрерывная в замкнутом интервале [α,b], график, которой схематически изображен на рисунке 3.7.1.

И нтеграл от этой функции – есть число, равное площади криволинейной трапеции, построенной на интервале [α,b] и ограниченной сверху графиком данной функции y=f(x). Рассмотрим интеграл, у которого изменяется верхняя граница (это указано стрелкой)

.

Тогда площадь под кривой f(x) также будет изменяться, по какому то закону. Иными словами, площадь криволинейной трапеции будет функцией верхнего предела (Рис.3.7.1), обозначим ее:

.

Следует обратить особое внимание на то, что аргументом функции Ф(х) является верхний предел, при этом переменная, стоящая под знаком интеграла пробегает все значения от α до x, и ее лучше обозначить другой буквой

.

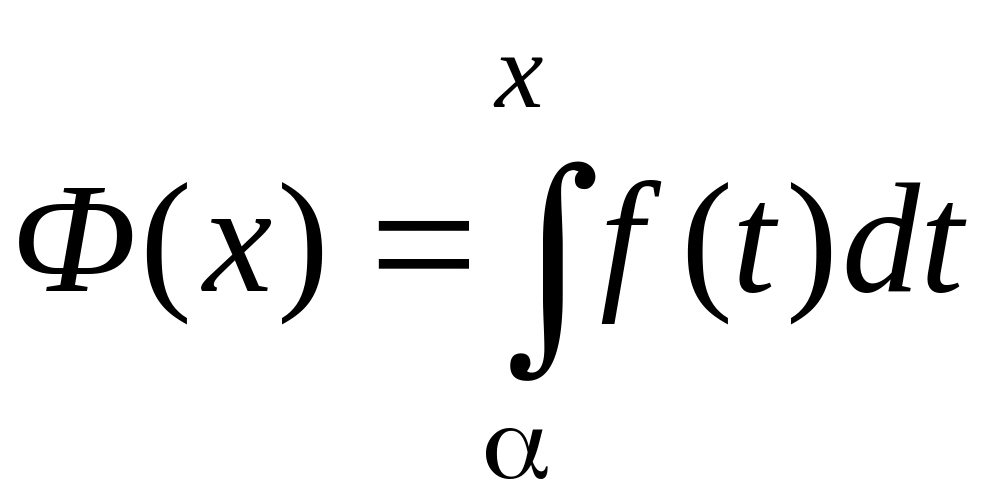Производная характеризует скорость изменения площади криволинейной трапеции и равна пределу отношения приращения функции к приращению аргумента при стремлении последнего к нулю.

Дадим приращение аргументу х+Δх, и найдем соответствующее приращение функции Ф(х):

В первом интеграле полученного равенства интервал интегрирования [α, x+Δx] разобьем на части, тогда:

Приращение функции Ф(х) по теореме о среднем будет равно

где х < ε < x+Δх.

Поделим найденное приращение функции на приращение аргумента и перейдем к пределу

.

При Δx → 0 точка ε стремится к точке х, т.е.:

Таким образом, производная от линейного интеграла с переменным верхним пределом оказалась равной значению подынтегральной функции в верхнем пределе интегрирования:

Отсюда следует, что интеграл

является одной из первообразных для подынтегральной функции f(t). Эта первообразная выражает переменную площадь под кривой f(t).

Итак, между определенным линейным и неопределенным интегралами существует связь, суть которой можно сформулировать следующим образом.

Интеграл называют определенным потому, что границы у него закреплены (определены). Как только верхний предел начинает двигаться (становиться неопределенным) линейный интеграл перестает быть определенным числом и превращается в одну из первообразных для функции f(t). Значения этой первообразной равны изменяющейся площади криволинейной трапеции, расположенной под кривой f(t).

3.7.2. Формула Ньютона-Лейбница

Неопределенный интеграл, согласно определению – это множество первообразных:

(3.7.1)

где С – произвольная постоянная.

В этом множестве находится и та первообразная, которая измеряет площадь под кривой f(t). Чтобы найти эту первообразную, нужно определить для нее значение постоянной С. Предположим, что постоянная равна С = С₁, тогда

(3.7.2)

Для нахождения С₁ воспользуемся тем, что первообразная пересекает ось Ох в точке х = α, так как ее значение в этой точке равно нулю:

(3.7.3)

Из равенства (3.7.3) следует: С₁= – F(α).

Подставим найденное значение постоянной в равенство (3.7.2), получим:

(3.7.4)

А теперь найдем величину линейного интеграла которая равна значению первообразной Ф(х) в точке х = b. Для этого в формуле (3.7.4) нужно положить верхний предел равным числу b:

(3.7.5)

Полученную формулу (3.7.5) называют формулой Ньютона-Лейбница. Она позволяет вычислять линейный интеграл с помощью неопределенного без непосредственного вычисления предела интегральных сумм. Число, которому равен линейный интеграл, есть приращение одной из первообразных на интервале интегрирования.

Поскольку, первообразные отличаются друг от друга на постоянную, то определенный линейный интеграл равен приращению любой из первообразных на [a,b].

Разность значений функции F(x) часто записывают так:

(3.7.6)

где знак – означает, что в функцию F(x) надо подставить вместо аргумента сначала верхний предел, затем нижний и из первого результата вычесть второй.

Найдем несколько простых интегралов с помощью полученной формулы.

1.

2.

3.

4.

5.

До сих пор считалось, что нижний предел в линейном интеграле меньше верхнего (α < b).

Для ряда случаев удобно распространить определение линейного интеграла, когда α > b. Если α > b, то будем считать, что

.

Тогда формула Ньютона-Лейбница будет верна и в этом случае:

.

Далее следует отметить, что вычисление линейного интеграла с помощью неопределенного по формуле Ньютона-Лейбница на практике не всегда возможно. Во-первых, первообразная может не выражаться через известные элементарные функции, т.е. не берется соответствующий неопределенный интеграл, либо первообразная не выражается через известные неэлементарные (специальные) функции. Во-вторых, найденная первообразная может оказаться очень громоздкой. И, наконец, функция, которую надо проинтегрировать, может быть задана не формулой, а например, таблицей значений или графиком. Во всех этих случаях линейный интеграл вычисляют приближенно с помощью численного интегрирования. Существует много различных способов и формул для приближенного вычисления линейного интеграла. Мы здесь рассматривать их не будем.