3.6.5. Свойства определенных интегралов

Так как свойства определенных интегралов всех типов одинаковы, то мы сформулируем и докажем их в общем случае для определенного интеграла в виде

где (Ω)– фигура или область интегрирования;

f(P) – функция, заданная на точках этой фигуры;

dΩ – мера элемента фигуры, который в пределе стягивается к точке.

Свойство 1. Постоянный множитель можно выносить за знак определенного интеграла, т.е.:

Свойство 2. Аддитивность по функции.

Интеграл от сумы конечного числа функций равен сумме интегралов от слагаемых функций.

Оба свойства доказываются с помощью свойств сумм и пределов.

Свойство 3. Аддитивность по фигуре.

Если область интегрирования (Ω) разбить на несколько частей, например , то определенный интеграл будет равен сумме интегралов по этим частям:

Доказательство. Докажем это свойство для линейного интеграла, исходя из его геометрического смысла.

Л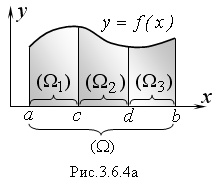 инейный интеграл равен площади криволинейной трапеции, ограниченной снизу отрезком [α,b], сверху графиком подынтегральной функции, с боков прямыми х = α, х = b (рисунок 3.6.4а).

Разобьем интервал интегрирования b – α = Ω на три части точками c и d: (рисунок 3.6.4 а).

Тогда площадь криволинейной трапеции, ограниченной снизу отрезком [α,b] разобьется на три части. Каждая часть этой площади также является криволинейной трапецией и поэтому равна линейному интегралу т.е.

Аналогичное доказательство можно привести для криволинейного и двойного интегралов.

Свойство 4. Если подынтегральная функция тождественно равна единице в области (Ω), то определенный интеграл равен мере фигуры:

Доказательство. В этом случае определенный интеграл есть предел интегральной суммы, состоящей только из мер элементарных частей, на которые разбита фигура. Складывая эти меры, получим меру фигуры:

На основании данного свойства определенные интегралы от функции будут равны:

линейный – длине интервала[α,b],

криволинейный – длине дуги кривой L,

двойной – площади плоской области D,

поверхностный – площади куска поверхности q,

тройной – объему пространственной области W.

Свойство 5. Если подынтегральная функция f(P) в области интегрирования (Ω) не меняет знак, то знак определенного интеграла совпадает со знаком функции, т.е.:

если f(P) ≥ 0, то

если f(P) ≤ 0, то

Доказательство. Пусть подынтегральная функция f(P) ≥ 0 для Тогда в интегральной сумме

все слагаемые будут неотрицательны, поэтому

Из данного свойства следует, что если во всех точках фигуры (Ω) для двух функций выполняется неравенство:

то

иными словами, неравенства можно интегрировать.

Доказательство. Перепишем неравенство двух функций в виде:

или

откуда следует:

.

Свойство 6. Оценка величины определенного интеграла. Если непрерывная функция f(P) в области интегрирования (Ω) принимает наименьшее значение равное m, а наибольшее значение равное М, то величина определенного интеграла заключена в пределах:

Доказательство. Поскольку m – наименьшее значение функции, а М – наибольшее, то все значения непрерывной функции заключены между числами:

Так как неравенства можно интегрировать, имеем:

Постоянные m и М вынесем за знак интегралов:

Интегралы от мер элементарных частей dΩ равны мере области интегрирования. С учетом этого окончательно получим:

Н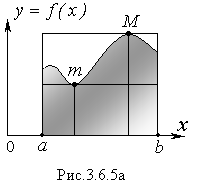 а основании данного свойства, можно приближено оценить величину определенного интеграла любого типа, если известны наибольшее и наименьшее значения подынтегральной функции, а также размеры области интегрирования.

Для линейного интеграла это свойство выглядит так:

Ему можно дать геометрическую иллюстрацию. Для этого на интервале [α,b] построим два прямоугольника с высотами, равными m и М, и криволинейную трапецию, ограниченную сверху графиком подынтегральной функции f(x) (рисунок 3.6.5а).

Площадь криволинейной трапеции (заштрихованная часть), равная интегралу

заключена между площадями двух прямоугольников с одним основанием длиной b – α, и разными высотами, равными числам m и М.

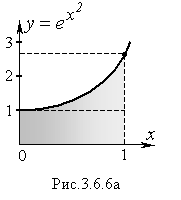
Пример 1. Найти числа, между которыми заключено значение линейного интеграла

Решение. Наименьшее значение функции на отрезке [0,1] равно – 1, наибольшее – е¹ = 2,7 (Рисунок 3.6.6а). Следовательно:

Свойство 7. Среднее значение функции.

За среднее значение функции, заданной на фигуре (или в области) (Ω), принимают величину интеграла от функции по фигуре, деленную на меру фигуры т.е.

Доказательство. Если дано n чисел то их средним арифметическим называют число:

Возникает вопрос, что считать средним значением функции f(P), заданной на фигуре (Ω), которая, вообще говоря, принимает бесконечное число значений? Чтобы найти , поступим следующим образом. Разобьем область(Ω)на n частей с равными мерами:

Внутри каждой элементарной части ( ) возьмем произвольную точку и вычислим в ней значение функции

.

Среднее арифметическое этих значений будет равно:

Поделим и умножим полученное выражение для среднего арифметического на размеры области (Ω) и перепишем его в виде:

За приближенное значение среднего функции в области (Ω) можно взять среднее арифметическое ее найденных значений. Заменяя на ∆Ω в последнем равенстве, получим:

Очевидно, что чем больше взято значений функции, тем точнее будет ее среднее значение в области (Ω). Увеличивая число разбиений, т.е. переходя к пределу при , получим:

Таким образом, найденное среднее функции равно определенному интегралу по области (Ω), деленному на меру области.

Осталось выяснить еще один вопрос, связанный с Принимает ли функция f(P) в какой либо точке фигуры (Ω) значение, равное ее среднему?

т.е. где

В тех случаях, когда f(P) непрерывна в замкнутой области (Ω), ответ положителен.

Свойство 8. Теорема о среднем.

Если функция f(P) непрерывна в замкнутой области (Ω), то найдется точка , в которой функция принимает значение, равное среднему:

где

Доказательство. Так как функция f(P) непрерывна в замкнутой области (Ω), то хотя бы в одной точке фигуры (Ω) она принимает наибольшее значение, равное числу М, и хотя бы в одной точке – наименьшее значение, равное числу m. Тогда величина определенного интеграла от этой функции по фигуре (Ω), согласно его свойствам, будет заключена между числами:

Поделим все части полученного неравенства на размеры фигуры (Ω):

Таким образом заключено между значениями функции в двух точках и Но непрерывная функция между двумя своими значениями принимает все промежуточные, в том числе и . Поэтому, обязательно найдется точка , в которой выполняется равенство

Теорему о среднем можно переписать в виде:

Это означает, что величина определенного интеграла от непрерывной функции f(P) по области (Ω) равна ее среднему значению, умноженному на размеры фигуры.

Д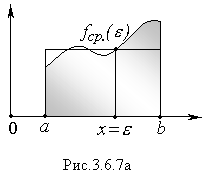 ля линейного интеграла теорема о среднем в последней форме записи выглядит так:

где

Геометрически это означает, что площадь криволинейной трапеции, равная линейному интегралу такая же как площадь прямоугольника, у которого основанием служит отрезок [α,b], а высотой – среднее значение функции (рисунок 3.6.7а), причем, функция свое среднее значение принимает в точке .

В случае разрывной функции может получится так, что во всех точках P [α,b] значения функции не равны ее среднему

Пример 2. Функция одного переменного задана на отрезке [0,1] выражением:

График функции изображен на рисунке 3.6.8.а. Найдем среднее значение функции на интервале [0,1] по формуле

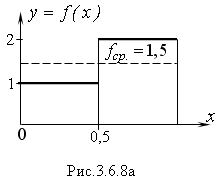
Длина интервала b – α = 1. На первой его половине , на второй – .

Поэтому интервал интегрирования разобьем на две части, тогда

Применяя свойства определенных интегралов, получим:

Ни в одной точке отрезка [0,1] данная функция не принимает значения, равного среднему: .

В заключении отметим, что в математической литературе замкнутый интервал [α,b] часто называют отрезком или сегментом, сохраняя термин “интервала” только для открытого (α,b).