3.6.3. Теорема о существовании определенного интеграла

Согласно определению, определенный интеграл – это число, равное пределу, к которому стремится интегральная сумма при увеличении числа разбиений фигуры на элементарные части. В тех случаях, когда предела нет или он бесконечен, определенный интеграл не существует.

Сформулируем теорему существования определенного интеграла, т.е. теорему существования конечного предела интегральной суммы. Теорема справедлива для интегралов всех типов. Поэтому, мы сформулируем ее в общем случае для определенного интеграла вида

Теорема. Если размеры фигуры (Ω) (отрезка прямой, плоской или объемной области) конечны, а функция заданная на ней, непрерывна во всех внутренних точках и на ее границе, то на данной фигуре существует определенный интеграл от заданной на ней функции.

Теорему легко переложить для конкретного интеграла любого типа, например, для линейного её формулируют так:

Если отрезок прямой [α,b] – конечен и функция f(x) непрерывна в замкнутом интервале [α,b], то на этом интервале существует линейный интеграл от заданной на нем функции f(x).

Примечание. Формулировка теоремы о существовании определенного интеграла приведена с усиленным ограничением на подынтегральную функцию (требование ее непрерывности). В таком виде эта теорема приводится в ряде учебников (Пискунов, Бермант и Араманович, Хавинсон). Однако, следует отметить, что определенный интеграл по конечной фигуре (Ω) или области существует и от разрывных функций, если эти функции в области (Ω) терпят разрывы первого рода (Смирнов, Мышкис, Липман Бер, Бугров и Никольский).

3.6.4. Геометрический смысл определенных интегралов

Начнем с линейного интеграла. Как уже отмечалось, этот интеграл представляет собой предел интегральной суммы составленной для функции одного переменного, заданной на конечном интервале [α,b]

Построим график подынтегральной функции и проведем прямые х = α и х = b до пересечения с этим графиком (рисунок 3.6.1 а). Фигуру, ограниченную снизу отрезку [α,b], сверху – графиком функции y = f(x), (которая предполагается положительной), а с боков прямыми х = α, х = b, называют криволинейной трапецией. Покажем, что линейный интеграл равен площади построенной криволинейной трапеции. Для этого, разобьем отрезок [α,b] на n частей: , с мерами , при этом мера i-го отрезка равна разности координат конечной и начальной точек

Внутри каждой части возьмем произвольные точки и построим прямоугольники с высотами: на соответствующих элементарных отрезках (рисунок 3.6.1 а). Площадь i-го прямоугольника будет равна i-му слагаемому интегральной суммы:

Следовательно, интегральная сумма линейного интеграла представляет собой сумму площадей прямоугольников, построенных на частичных интервалах с длинами , и с высотами . Сумма этих площадей дает площадь фигуры, ограниченной сверху ступенчатой линией, с боков прямыми х = α, х = b, а снизу отрезком [α,b].

В пределе, при стремлении к нулю наибольшей длины частичного интервала , ступенчатая линия приближается к графику подынтегральной функции.

Таким образом, если интегрируемая функция f(x) не отрицательна, то линейный интеграл 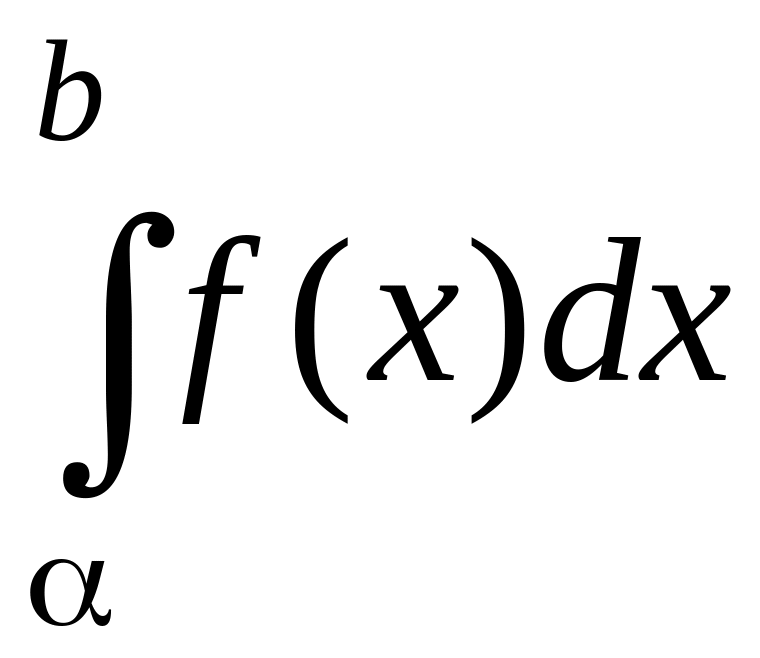равен площади соответствующей криволинейной трапеции. В общем случае, когда f(x) может принимать как положительные, так и отрицательные значения, линейный интеграл дает алгебраическую сумму площадей получающихся криволинейных трапеций. В эту сумму площади криволинейных трапеций, лежащих над осью Ох, войдут со знаком «плюс», а площади криволинейных трапеций, расположенных под осью Ох – со знаком «минус».

Рассмотрим криволинейный интеграл по плоской кривой.

Он равен пределу интегральной суммы вида:

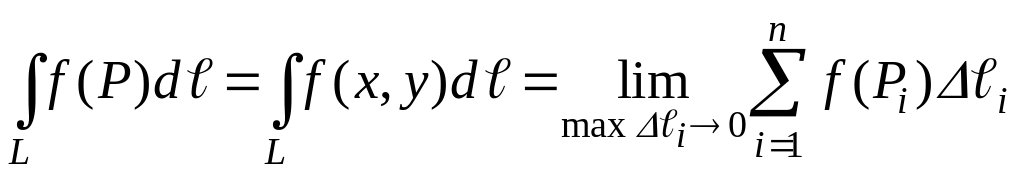
Пусть плоская линия L часть графика некоторой функции одного переменного , расположенной между точками α(х_1,y₁) и b(х_2,y₂) на плоскости xOy (рисунок 3.6.2 а). На точках этой линии задана функция двух переменных . Предположим, что она положительна и является линейной плотностью массы.

Функцию называют подынтегральной, ее графиком является поверхность в пространстве (рисунок 3.6.2.а).

Подынтегральную функцию не следует путать с уравнением линии .

Построим на кривой L часть цилиндрической поверхности с образующей, параллельной оси Оz, и отсеченной сверху графиком подынтегральной функции.

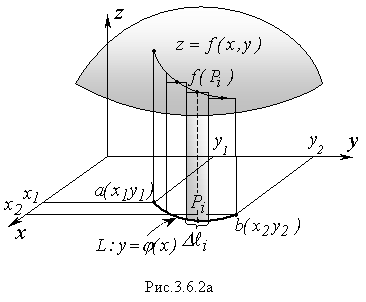
Покажем, что площадь этой поверхности будет равна криволинейному интегралу.

Для этого, разобьем линию L на n частей с длинами , а цилиндрическую поверхность соответственно на n узких полосок. Каждую полоску можно принять за прямоугольник с основанием и высотой, равной значению подынтегральной функции в точке (рисунок 3.6.2 а). Площадь i-го прямоугольника будет равна i-му слагаемому в интегральной сумме

Следовательно, интегральная сумма криволинейного интеграла, равная сумме площадей всех полосок, дает площадь части цилиндрической поверхности, отрезанной сверху пространственной ломаной линией. В пределе при ступенчатая линия приближается к линии пересечения цилиндрической поверхности и графика подынтегральной функции f(x,y). В результате, криволинейный интеграл, равный пределу интегральной суммы, дает площадь части цилиндрической поверхности с направляющей линией L и образующей, параллельной оси Oz, срезанной сверху графиком подынтегральной функции.

Перейдем к двойному интегралу по плоской области D. Он также равен пределу интегральной сумы вида:

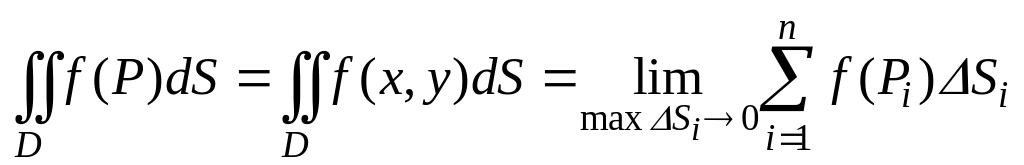
где – мера элементарной части, на которые разбита область D.

Ч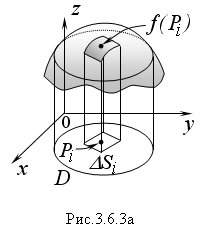 тобы выяснить геометрический смысл двойного интеграла, построим область D и цилиндрическую поверхность с направляющей, которая является границей области D, и образующей, параллельной оси Oz.

Будем считать, что подынтегральная функция неотрицательна во всех точках области D, тогда ее график отсечет цилиндрическую поверхность сверху.

В результате получится цилиндрическое тело, ограниченное снизу областью D, с боков – цилиндрической поверхностью, а сверху – графиком подынтегральной функции (рисунок 3.6.3 а).

От обычного цилиндра оно будет отличаться тем, что сверху ограничено не плоскостью, параллельной плоскости xOy, а поверхностью. Покажем, что двойной интеграл по области D равен объему полученного тела.

Для этого разобьем область D на n частей:

с мерами . В результате тело разобьется на узкие цилиндрические тела. В каждой элементарной части возьмем произвольную точку и вычислим в ней значение подынтегральной функции .

Рассмотрим произведение – оно равно объему цилиндра с основанием и высотой (рисунок 3.6.3 а).

Объем i-го кусочка тела можно приближенно взять за объем цилиндра, т.е.:

Тогда объем всего цилиндрического тела приближенно будет равен сумме .

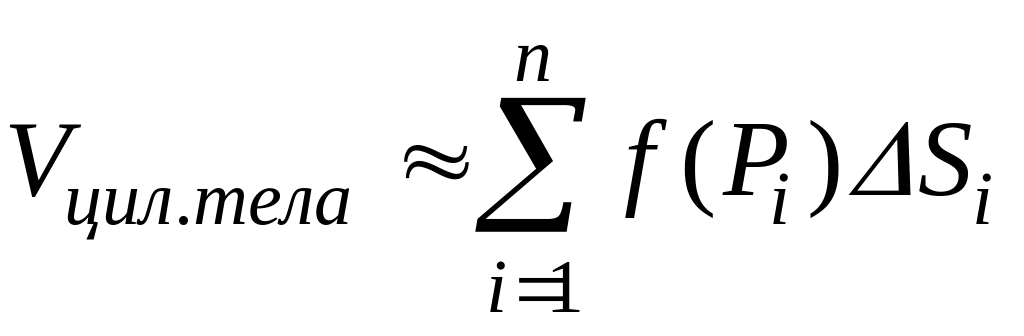Чтобы получить точное значение объема, нужно перейти к пределу

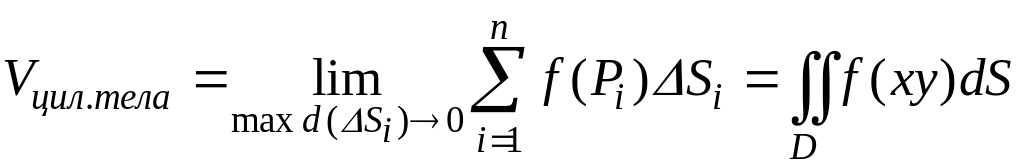
Таким образом, двойной интеграл – это число, равное объему цилиндрического тела, ограниченного снизу областью D, с боков цилиндрической поверхностью, сверху графиком подынтегральной функции.

В заключении следует отметить, что тройной и поверхностный интеграл для произвольной интегрируемой функции f(P) не имеют простого геометрического смысла. Если функцию f(P) считать плотностью массы, то тройному и поверхностному интегралам можно дать интерпритацию как массы фигур.