Министерство образования и науки Российской Федерации

Федеральное агентство образования

Негосударственное образовательное учреждение высшего профессионального образования «Технологический институт «вту»»

Факультет техники и технологий

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ

по дисциплине «Специальные главы прикладной математики»

Разработка программной оболочки методов решения задач

многомерного статистического анализа

Руководитель

______________ Соловьев Н. А.

«___» _______________ 2012 г.

Исполнитель

студент группы : БСИТ ПО-309

________________ Клоков А.И.

«___» ________________ 2012 г.

Оренбург 2012

Содержание

Введение………………………………………………………………….…….….3

1. Описание метода решения задачи многомерного статического анализа...4

2. Выбор и обоснование инструментальных средств программирования.…6

3. Разработка иерархических модулей программного продукта……….…...7

4. Разработка алгоритмов решения задачи и его программного кода……...8

5. Тестирование разработанного программного продукта…………………10

Заключение………………………………………………………….….…….….16

Список используемых источников….……………….…………………………17

Приложение а – Листинг программы………………………………………..…18

Введение

Целью расчетно-графического задания является разработка программной оболочки обработки информационных процессов матричных преобразований. Матрица — математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Иногда рассматривают многомерные матрицы или матрицы непрямоугольной формы.

Для достижения цели необходимо решить ряд инженерных задач по направлению информатика и вычислительная техника.

Решение инженерных задач основывается на методах:

1. Специальных главах прикладной математики;

2. Программирование на языке высокого уровня;

3. Объектно-ориентированное программирование;

4. Информатики.

1. Описание метода решения задачи многомерного статического анализа.

Для выбора аппарата статистического анализа для решения поставленной задачи был проведен краткий обзор наиболее распространенных из существующих методов статистического анализа. Исследовав их, был определен вывод, что для решения понадобится один из методов кластерного анализа.

Кластерный анализ – это совокупность методов многомерной классификации, целью которой является образование групп (кластеров) схожих между собой объектов. В отличие от традиционных группировок, рассматриваемых в общей теории статистики, кластерный анализ приводит к разбиению на группы с учетом всех группировочных признаков одновременно. Например, если наблюдаемый объект характеризуется двумя признаками и , то при использовании методов кластерного анализа оба эти признака учитываются одновременно при отнесении наблюдения в ту или иную группу /3/. Методы кластерного анализа позволяют решать следующие задачи:

• проведение классификации объектов с учетом признаков, отражающих сущность, саму природу объектов;

• проверка выдвигаемых предположений о наличии некоторой структуры в изучаемой совокупности объектов, т.е. поиск существующей структуры;

• построение новых классификаций для слабо изученных явлений, когда необходимо установить наличие связей внутри совокупности и попытаться привнести в нее структуру.

Для записи формализованных алгоритмов кластерного анализа введем следующие условные обозначения:

– совокупность объектов наблюдения; – i-е наблюдение в m-мерном пространстве признаков ( ); – расстояние между -м и -м объектами; – нормированные значения исходных переменных; – матрица расстояний между объектами.

Для реализации любого метода кластерного анализа необходимо ввести понятие «сходство объектов». Причем в процессе классификации в каждый кластер должны попадать объекты, имеющие наибольшее сходство друг с другом с точки зрения наблюдаемых переменных.

В кластерном анализе для количественной оценки сходства вводится понятие метрики. Каждый объект описывается -признаками и представлен как точка в -мерном пространстве. Сходство или различие между классифицируемыми объектами устанавливается в зависимости от метрического расстояния между ними. В кластерном анализе используются различные меры расстояния между объектами:

• -евклидово расстояние;

• -взвешенное евклидово расстояние;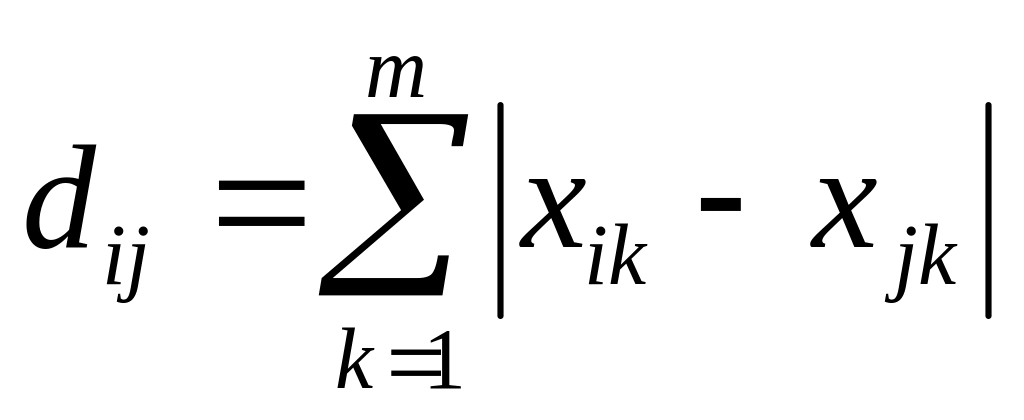

• -расстояние city-block;

• -расстояние Минковского;

• -расстояние Махаланобиса ,

где – расстояние между -ым и -ым объектами; , – значения -переменной и соответственно у -го и -го объектов; , – векторы значений переменных у -го и -го объектов; – общая ковариационная матрица; – вес, приписываемый -й переменной.

Классифицированные процедуры иерархического типа предназначены для получения наглядного представления о структуре исследуемой совокупности объектов. Эти процедуры основаны на последовательном объединении кластеров (алгомеративные процедуры).

Процесс поиска представляет собой процедуру определения «ближайшего» (наилучшего) кластера и определения наилучших условий.

На первом шаге все объекты считаются отдельными кластерами. Затем на каждом последующем шаге два ближайших кластера объединяются в один. Каждое объединение уменьшает число кластеров на один так, что в конце концов все объекты объединяются в один кластер. В результате создается дендограмма - отображает результат группирования объектов на всех шагах алгоритма.