§4.4. Элементарные преобразования матриц.

4.4.1. Определение. Элементарными называются следующие преобразования матриц:

• перестановка строк местами;

• умножение строки на отличное от нуля число;

• прибавление к каждому элементу строки соответствующего элемента другой строки;

• те же преобразования столбцов.

4.4.2. Определение. Матрицы называются эквивалентными, если одна из них может быть получена из другой с помощью элементарных преобразований.

4.4.3. Алгоритм приведения матрицы к ступенчатому виду с помощью элементарных преобразований строк.

1. Выбираем текущий элемент. Начинаем с элемента, расположенного в левом верхнем углу матрицы. Если он равен нулю, то просматриваем элементы, расположенные под текущим элементом. Если среди них нет ненулевых элементов, то смещаемся на 1 элемент вправо и т.д. Если же среди элементов, расположенных под рассматриваемым элементом, есть ненулевой, то меняем местами строки так, чтобы текущий элемент был отличен от нуля.

2. На предыдущем этапе алгоритма мы добились того, чтобы текущий элемент был отличен от нуля. Теперь просматриваем элементы, расположенные в столбце под текущим ненулевым элементом: если среди них есть ненулевые, то с помощью элементарных преобразований соответствующих строк обращаем их в нули.

3. Если в столбце под текущим ненулевым элементом расположены лишь нулевые элементы, то смещаемся на один столбец вправо и на одну строку вниз. И так далее.

Замечание.

Так как число строк и столбцов матрицы конечно, то алгоритм может быть реализован за конечное число шагов.

Пример.

Приведем матрицу к ступенчатому виду с помощью элементарных преобразований строк:

.

§4.5. Блочные матрицы

4.5.1. Определение. Пусть матрица с помощью горизонтальных и вертикальных линий разбита на отдельные прямоугольные клетки, каждая из которых в свою очередь является матрицей меньших размеров. Тогда всякая клетка называется блоком исходной матрицы, а сама матрица называется блочной.

Пример.

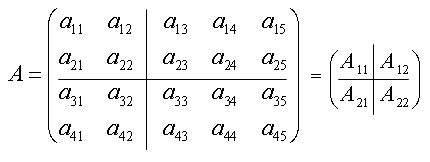
Замечание.

Основные операции (сложение, умножение на число, умножение, транспонирование), в случае, если они определены, будут выполняться для блоков так же, как и для элементов обычных матриц.

§ 4.6. Прямая сумма квадратных матриц.

4.6.1. Определение. Прямой суммой квадратных матриц размера и размера называется блочная матрица размера вида

4.6.2. Теорема. (Свойства операции прямой суммы квадратных матриц)

Для произвольных квадратных матриц и справедливо:

1.

Для произвольных квадратных матриц размера и матриц размера имеют место следующие свойства:

2.

3.

Доказательство:

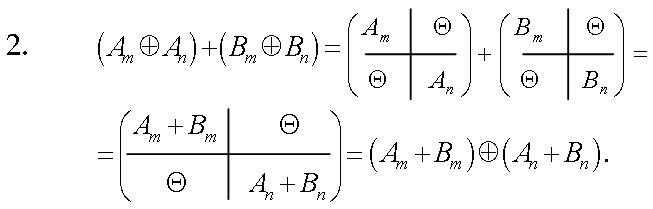
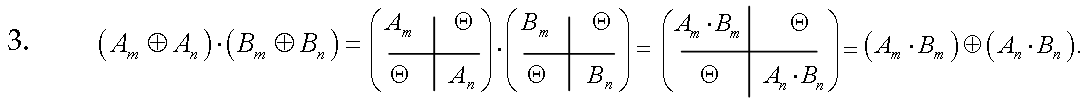
§4.7. Обратная матрица

4.7.1. Определение. Пусть − квадратная матрица размера , − единичная матрица того же размера. Матрица называется левой обратной по отношению к , если . Матрица называется правой обратной по отношению к , если .

4.7.2. Теорема. (О единственности обратной матрицы)

Если для квадратной матрицы существуют ее левая и правая обратные матрицы, то они совпадают.

Доказательство:

Пусть − правая, а − левая обратные матрицы для матрицы. Тогда

Замечание. Поскольку левая и правая обратные матрицы совпадают, то имеет смысл ввести понятие обратной матрицы, т.е. . Таким образом, матрица называется обратной по отношению к матрице , если

4.7.3. Определение. Квадратная матрица , у которой существует обратная матрица , называется обратимой.

4.7.4. Определение. Квадратная матрица , определитель которой отличен от нуля, называется невырожденной. В противном случае матрица называется вырожденной.

4.7.5. Теорема. (Критерий существования обратной матрицы)

Для того, чтобы квадратная матрица была обратимой, необходимо и достаточно, чтобы она была невырожденной.

Доказательство:

Необходимость.

Пусть матрица обратима, следовательно, существует обратная матрица . Тогда по теореме 4.3.6 об определителе произведения квадратных матриц

следовательно, , то есть матрица является невырожденной.

Достаточность.

Пусть теперь матрица является невырожденной, то есть .

Рассмотрим матрицу

, (4.1)

где − алгебраическое дополнение элемента матрицы . Покажем, что матрица является обратной по отношению к матрице . Рассмотрим их произведение :

Следовательно, произведение матрицы на равно единичной матрице. Аналогично показывается, что произведение матрицы на есть единичная матрица, а это означает, что матрица является обратной по отношению к матрице .

Теорема доказана.

4.7.6. Определение. Матрица, являющаяся транспонированной по отношению к матрице, составленной из алгебраических дополнений соответствующих элементов матрицы , называется присоединенной для матрицы и обозначается .

Замечание. Метод нахождения обратной матрицы с помощью формулы (1) называется методом присоединенной матрицы.

Пример.

Найдем обратную матрицу для матрицы .

Вычисляем присоединенную матрицу и определитель исходной матрицы:

, ,

следовательно,

4.7.7. Теорема. (Об обратной матрице произведения матриц)

Матрица, обратная произведению двух матриц, равна произведению их обратных матриц, взятых в обратном порядке:

Доказательство:

Пусть − невырожденные квадратные матрицы одного порядка. Тогда по теореме 4.3.6 об определителе произведения квадратных матриц их произведение также является невырожденной матрицей. Следовательно, по теореме 4.7.5 существуют обратные матрицы Рассмотрим произведение

Аналогично

Следовательно, матрица является обратной по отношению к произведению матриц .

4.7.8. Теорема. (О матрице, обратной к транспонированной матрице)

Если квадратная матрица обратима, то и обратимой является и ее транспонированная матрица, причем

Доказательство:

Очевидно, что матрица при транспонировании остается невырожденной, следовательно, у нее существует обратная матрица. Легко проверить, что

что и доказывает утверждение теоремы.

Лекция 12

4.7.9. Нахождение обратной матрицы с помощью элементарных преобразований.

Обратную матрицу можно также найти с помощью элементарных преобразований строк исходной матрицы . Для этого требуется составить блочную матрицу , а затем с помощью элементарных преобразований строк привести эту блочную матрицу к виду . Полученная матрица и будет обратной по отношении к матрице .

Пример.

Найдем обратную матрицу для матрицы .

Преобразуем блочную матрицу

Таким образом,

4.7.10. Решение матричных уравнений.

Рассмотрим основные виды матричных уравнений:

, ,

где − квадратная невырожденная матрица.

Решением матричного уравнения называется такая матрица , которая при подстановке в матричное уравнение обращает его в тождество.

Умножим обе части уравнения слева на обратную матрицу :

,

откуда

.

Аналогично, при умножении обеих частей уравнения справа на матрицу , найдем решение

.

Замечание.

Для уравнения , где , − квадратные невырожденные матрицы соответствующих размеров решение имеет вид:

.

4.7.11. Решение систем линейных алгебраических уравнений (СЛАУ).

4.7.11.1. Матричный способ.

Рассмотрим квадратную систему линейных алгебраических уравнений

(4.2)

Вводя в рассмотрение матрицу коэффициентов системы , столбец неизвестных и столбец свободных членов

Перепишем систему уравнений (4.2) в виде матричного уравнения . Отсюда решение СЛАУ имеет вид

. (4.3)

4.7.11.2. Формулы Крамера.

Заметим, что непосредственно из формулы (4.3) вытекают формулы Крамера.

Обозначим и запишем решение (4.3) в явном виде:

.

Величина по традиции служит для обозначения определителя, у которого столбец заменен на столбец свободных членов системы.

Замечание. Матричный способ и формулы Крамера применимы лишь для СЛАУ в случае невырожденной квадратной матрицы системы .