Лекция 14

Глава 5. Системы линейных алгебраических уравнений.

§5.1. Основные понятия.

5.1.1. Определение. Системой m линейных алгебраических уравнений (СЛАУ) с n неизвестными называется система уравнений вида

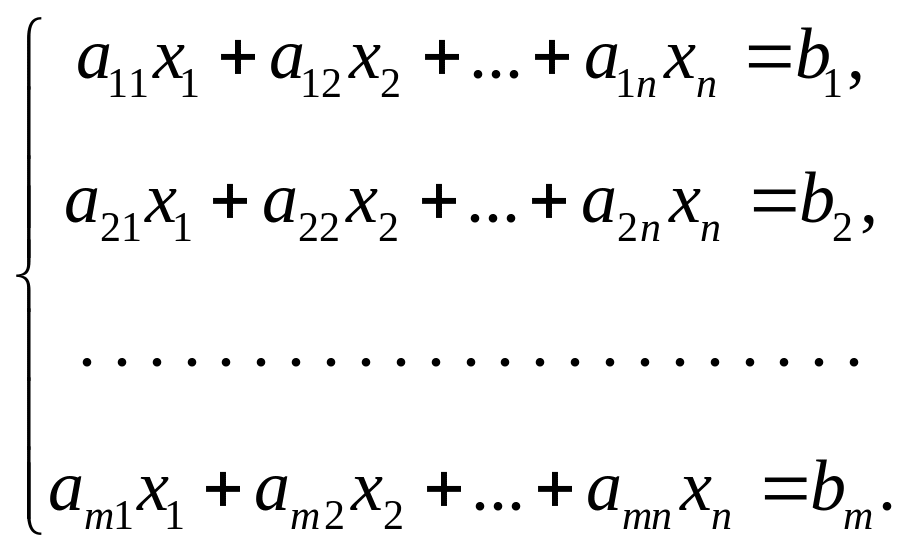(5.1)

Величины , называемые свободными членами уравнений, и , называемые коэффициентами системы, предполагаются известными, а величины − неизвестными, подлежащими определению. Каждый коэффициент имеет два индекса, первый из которых обозначает номер уравнения, а второй – номер неизвестного, при котором находится этот коэффициент.

5.1.2. Определение. Система линейных алгебраических уравнений называется однородной, если свободные члены всех ее уравнений равны нулю, то есть . В противном случае, то есть если найдется уравнение с отличным от нуля свободным членом, система называется неоднородной.

5.1.3. Определение. Система линейных алгебраических уравнений называется квадратной, если число составляющих ее уравнений равно числу неизвестных .

5.1.4. Определение. Решением системы линейных алгебраических уравнений (5.1) называется упорядоченная совокупность чисел , которые при подстановке в систему обращает каждое ее уравнение в тождество.

Замечание. Удобно также записывать решения системы (5.1) в виде столбцов: .

5.1.5. Определение. Система линейных алгебраических уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения.

Замечание. Два решения системы линейных алгебраических уравнений и называются различными, если нарушается хотя бы одно из равенств .

5.1.6. Определение. Совместная система линейных алгебраических уравнений называется определенной, если она имеет единственной решение.

5.1.7. Определение. Совместная система линейных алгебраических уравнений называется неопределенной, если она имеет хотя бы два различных решения.

5.1.8. Определение. Совокупность всех решений системы линейных алгебраических уравнений (5.1) называется ее общим решением.

5.1.9. Определение. Матрица коэффициентов системы линейных алгебраических уравнений (5.1) называется основной матрицей системы.

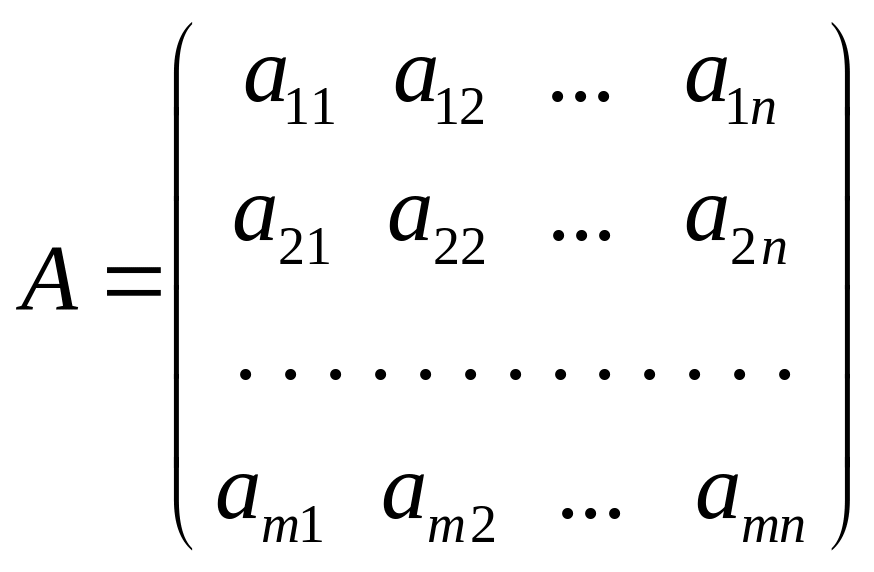
5.1.10. Определение. Блочная матрица вида

называется расширенной матрицей системы (5.1).

5.1.11. Матричная форма записи системы линейных алгебраических уравнений.

Введем в рассмотрение столбец неизвестных и столбец свободных членов . Заметим, что система (5.1) может быть записана в виде

.

Это представление называется матричной формой записи системы линейных алгебраических уравнений.

5.1.12. Векторная форма записи системы линейных алгебраических уравнений.

Рассмотрим расширенную матрицу системы как совокупность столбцов матрицы как векторов

Тогда система (5.1) может быть представлена в форме

,

которая называется векторной формой записи системы линейных алгебраических уравнений.

§5.2. Решение неоднородных систем

линейных алгебраических уравнений.

5.2.1. Теорема Кронекера-Капелли (Критерий совместности системы линейных алгебраических уравнений)

Для того, чтобы система линейных алгебраических уравнений (5.1) была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу основной матрицы системы:

.

Доказательство:

Необходимость.

Пусть система (5.1) совместна. Запишем систему в векторной форме

.

Пусть совокупность чисел является решением системы. Следовательно, имеет место равенство

.

Обозначим , пусть − базисные столбцы. Тогда последнее равенство означает, что столбец свободных членов является линейной комбинацией базисных столбцов, то есть являются базисными столбцами и для расширенной матрицы. Следовательно, .

Достаточность.

Пусть , − базисные столбцы. Заметим, что столбец свободных членов не может быть базисным, иначе условие не выполняется. Следовательно, столбец может быть представлен в виде линейной комбинации базисных столбцов, то есть существуют числа

.

Полагая запишем

.

Таким образом, − решение системы (5.1), то есть система совместна.

5.2.2. Нахождение всех решений совместной неоднородной системы линейных алгебраических уравнений.

Пусть система (5.1) является совместной, тогда согласно теореме Кронекера-Капелли . Предположим без ограничений общности, что базисный минор расширенной матрицы системы расположен в левом верхнем углу. Тогда первые r уравнений соответствуют базисным строкам, а оставшиеся уравнений являются их следствиями и могут быть исключены из дальнейшего рассмотрения. Запишем первые r уравнений, оставив в левой части лишь первые r переменных, соответствующих базисным столбцам:

(5.2)

Заметим, что систему уравнений (5.2) можно рассматривать относительно неизвестных при произвольных значениях переменных . Поэтому можно считать эти переменные произвольными постоянными, положив Заметим также, что матрица получившейся системы (5.2) относительно неизвестных является невырожденной, поскольку ее определителем является базисный минор

следовательно, ее решение может быть найдено по формулам Крамера:

Используя свойства определителя и обозначая определитель, в котором столбец заменен на столбец , через , перепишем последнюю форму в виде:

(5.3)

Легко показать, что формулы (5.3) задают все решения совместной системы линейных алгебраических уравнений (5.1). Действительно, пусть числа образуют решение системы (5.1), тогда они являются решением системы (5.2), следовательно, значения однозначно определяются формулами (5.3) при .

Замечание 1. Переменные обычно называют базисными, а переменные  свободными.

Замечание 2. В случае системы линейных алгебраических уравнений, у которой , число свободных переменных, очевидно, будет равно нулю. Следовательно, из формул (5.3) получим единственное решение системы, то есть система будет определенной.

Таким образом, для того, чтобы система линейных алгебраических уравнений имела единственное решение, необходимо и достаточно, чтобы число неизвестных не превышало числа уравнений и чтобы ранг расширенной матрицы системы был равен рангу основной матрицы системы и был равен числу неизвестных:

, .

Пример.

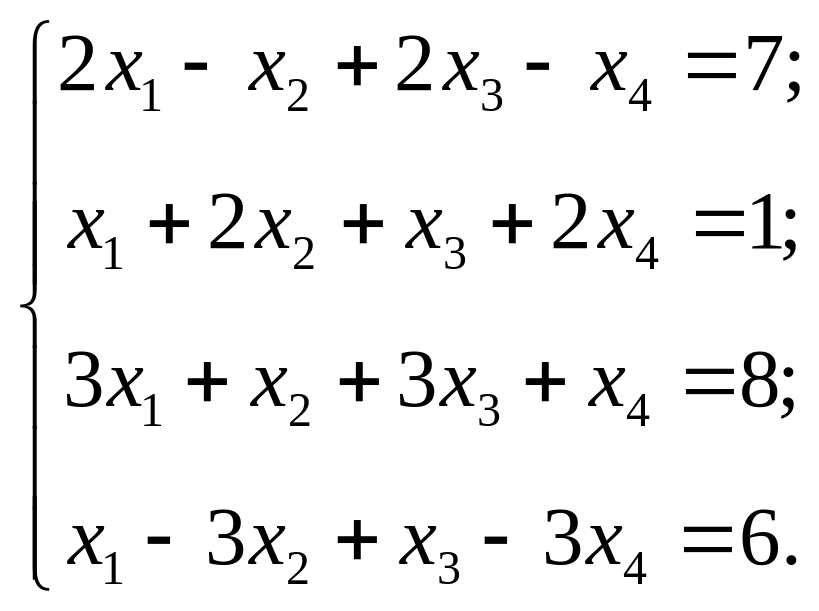
Исследуем, является ли система совместной:

.

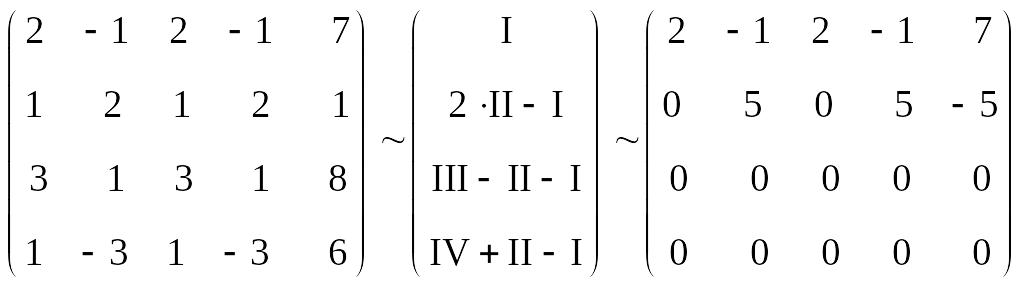
Следовательно, , то есть на основании теоремы Кронекера-Капелли система является совместной.

Выберем в качестве базисного минор, образованный пересечением строк 1 и 2 и столбцов 1 и 2:

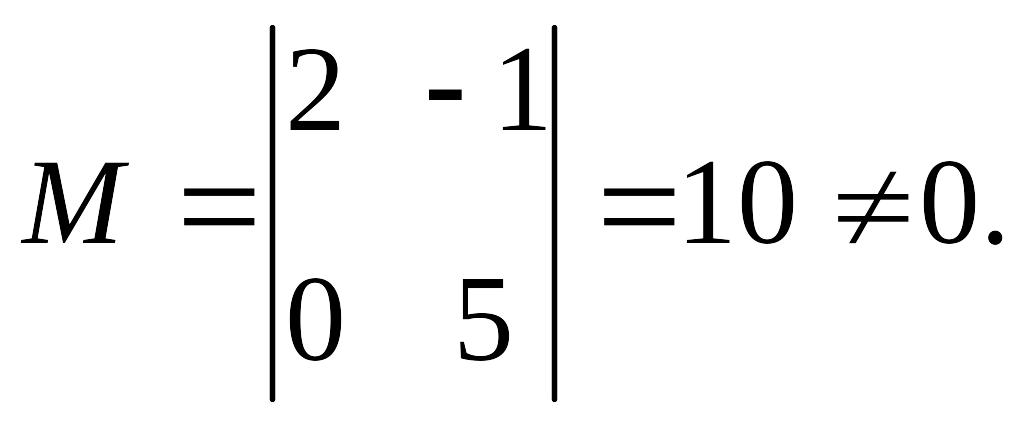
Следовательно, переменные будут базисными, а  свободными. Перепишем уравнения, полагая :

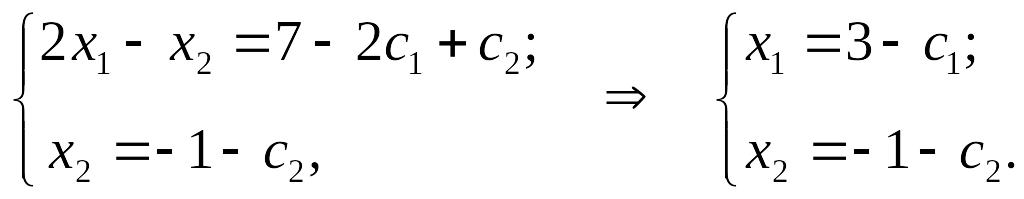
Таким образом, решение системы имеет вид:

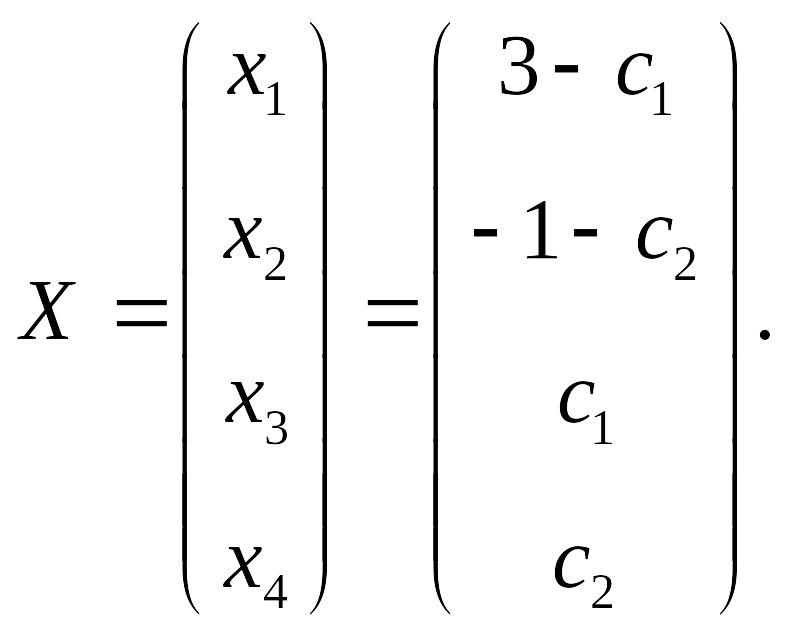
Лекция 15