§ 5.4. Связь между решениями неоднородной системы
линейных алгебраических уравнений и решениями
соответствующей ей однородной системы.
5.4.1. Теорема. Сумма произвольного решения неоднородной системы (5.1) и произвольного решения соответствующей однородной системы (5.4) является решением неоднородной системы (5.1).
Доказательство:
Пусть
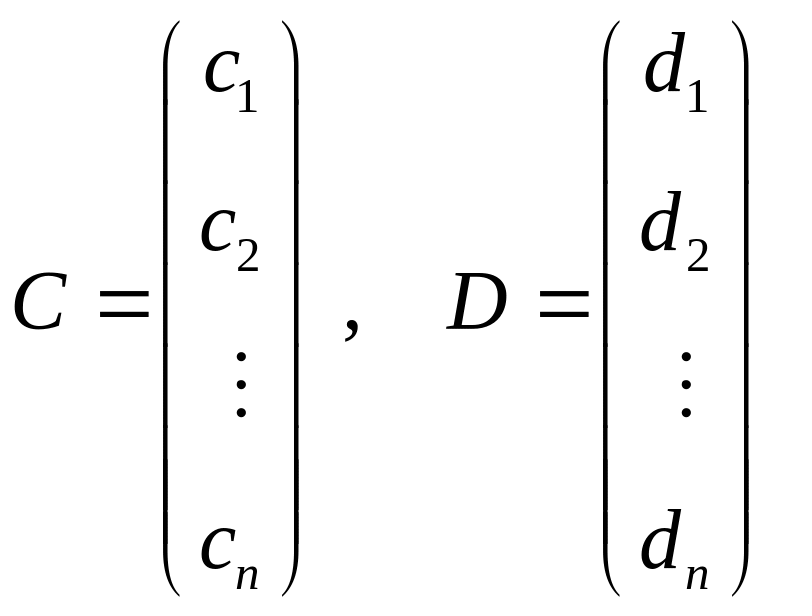
решения неоднородной и
однородной систем (5.1) и (5.4), соответственно.
Тогда в векторной форме
Складывая последние векторные равенства, получим:
что и доказывает теорему.
5.4.2. Теорема. Разность двух произвольных решений неоднородной системы (5.1) является решением соответствующей однородной системы (5.4).
Доказательство:
Пусть
решения неоднородной системы (5.1), следовательно,
Вычитая равенства, получим
что и доказывает теорему.
Замечание. Из теорем 5.4.1, 5.4.2 вытекает, что при сложении одного из решений неоднородной системы (5.1) со всеми решениями однородной системы (5.4) мы получим все решения исходной системы (5.1).
Теорема 5.4.3. (О структуре решения неоднородной системы линейных алгебраических уравнений)
Сумма частного решения неоднородной системы линейных алгебраических уравнений с общим решением соответствующей однородной системы является общим решением неоднородной системы.
Доказательство вытекает из теорем 5.4.1 и 5.4.2.
Таким образом, общее решение системы (5.1) имеет вид
где
некоторое частное решение системы
(5.1), а
фундаментальная
система решений соответствующей
однородной системы (5.4).
Пример.
Исследуем, является ли система совместной:
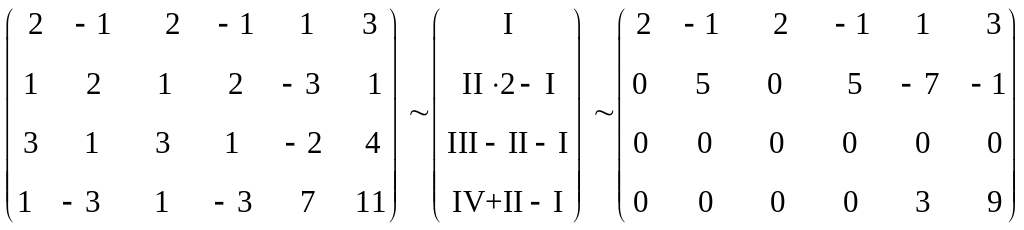
Поскольку
,
то система совместна. Выбираем базисный
минор
,
соответствующий базисным
переменным
и
.
Тогда свободные переменные
.
Соответствующая система уравнений
имеет вид
Таким образом, решение системы имеет вид:
Легко видеть, что первый столбец полученного решения является частным решением неоднородной системы, а оставшаяся линейная комбинация – общее решение соответствующей однородной системы, записанное в терминах нормальной фундаментальной системы решений.
5.4.4. Процедура решения системы линейных алгебраических уравнений.
Таким образом, последовательное решение системы линейных алгебраических уравнений выглядит следующим образом:
Составляем расширенную матрицу системы, приводим ее элементарными преобразованиями к ступенчатому виду и исследуем, выполняется ли условие
?а) Если
,
то система несовместна, решений нет.
б) Если
,
то система является определенной, то
есть
имеет единственное решение.
в) Если
,
то система имеет бесконечное множество
решений.
В случае совместности системы выделяем базисный минор, и соответствующие базисные переменные, полагаем свободные переменные произвольным постоянным и выражаем базисные переменные через свободные.
5.4.5. Метод Гаусса решения систем линейных алгебраических уравнений.
Метод Гаусса также называется методом последовательного исключения неизвестных. Фактически он включает в себя приведение расширенной матрицы системы элементарными преобразованиями к ступенчатому виду (прямой ход метода Гаусса) и исследование совместности системы, а затем последовательное определение базисных переменных через свободные переменные (обратный ход метода Гаусса).