
Динамика материальной системы и твердого тела
Центр
масс (центр
инерции) – геометрическая точка,
радиус-вектор
![]() которой определяется равенством:
которой определяется равенством:
![]() ,
где
,
где
![]() –
радиусы-векторы точек, образующих
систему. Координаты центра масс:
–
радиусы-векторы точек, образующих
систему. Координаты центра масс:
![]() и т.д. Дифф-ные
ур-ния движения системы матер.точек:
и т.д. Дифф-ные
ур-ния движения системы матер.точек:
![]() или в проекциях на оси координат:
или в проекциях на оси координат:
![]() и т.д. для каждой точки (тела) системы.
Момент инерции матер.точки:
mh2.
Момент инерции
тела: Jz=
mkhk2.
При непрерывном распределении масс:
Jx=
(y2+z2)dm;
Jy=
(z2+x2)dm;
Jz=
(x2+y2)dm.
Jz=
M2,
– радиус инерции тела. Полярный момент
инерции Jo=
(
x2+y2+z2)dm;
Jx+Jy+Jz=
2Jo.
Центробежный
момент инерции:
Jxy=xy
dm;
Jyz=yz
dm;
Jzx=zx
dm.
Jxy=Jyx
и т.д. для каждой точки (тела) системы.
Момент инерции матер.точки:
mh2.
Момент инерции
тела: Jz=
mkhk2.
При непрерывном распределении масс:
Jx=
(y2+z2)dm;
Jy=
(z2+x2)dm;
Jz=
(x2+y2)dm.
Jz=
M2,
– радиус инерции тела. Полярный момент
инерции Jo=
(
x2+y2+z2)dm;
Jx+Jy+Jz=
2Jo.
Центробежный
момент инерции:
Jxy=xy
dm;
Jyz=yz
dm;
Jzx=zx
dm.
Jxy=Jyx
Тензор
инерции в данной точке:

Моменты
инерции стержня:
![]()
![]() ;
;
![]() .
Сплошной диск:
.
Сплошной диск:
![]() .
.
Полый
цилиндр:![]() ,
цилиндр с массой распределенной по
ободу (обруч):
,
цилиндр с массой распределенной по
ободу (обруч):
![]() .
Теорема
Гюйгенса-Штейнера:
.
Теорема
Гюйгенса-Штейнера:
![]() .
Момент инерции относительно произвольной
оси: J
= Jxcos2
+ Jycos2
+ Jzcos2
– 2Jxycoscos
– 2Jyzcoscos
– 2Jzxcoscos,
если координатные оси – главные, то: J
= Jxcos2
+ Jycos2
+ Jzcos2.
.
Момент инерции относительно произвольной
оси: J
= Jxcos2
+ Jycos2
+ Jzcos2
– 2Jxycoscos
– 2Jyzcoscos
– 2Jzxcoscos,
если координатные оси – главные, то: J
= Jxcos2
+ Jycos2
+ Jzcos2.
Теорема о движении центра масс системы:
![]() .
дифференциальное уравнение движения
центра масс:
.
дифференциальное уравнение движения
центра масс:
![]() .
.
Закон
сохранения движения центра масс.
Если
![]()
![]() ,
если при этом в начальный момент vCx0=
0, то
,
если при этом в начальный момент vCx0=
0, то
![]()
xC=
const.
Количество
движения системы
xC=
const.
Количество
движения системы
![]() .
Теорема об
изменении количества движения системы:
.
Теорема об
изменении количества движения системы:
![]() ,
проекциях:
,
проекциях:
![]() .
Теорема об изменении кол-ва движения
системы в интегральной форме:
.
Теорема об изменении кол-ва движения
системы в интегральной форме:
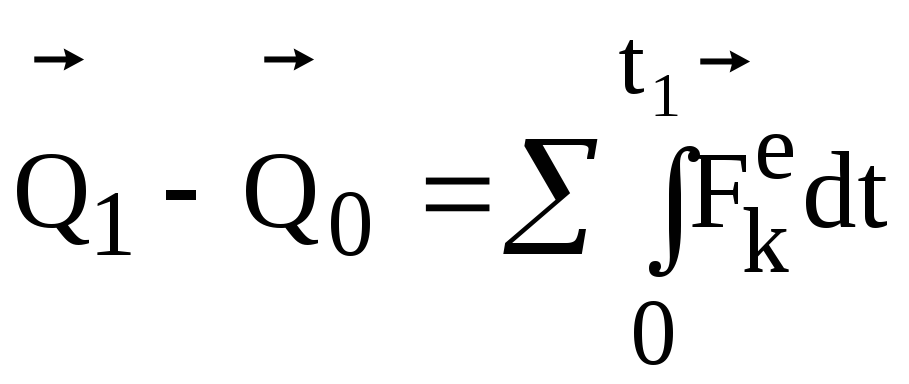 .
.
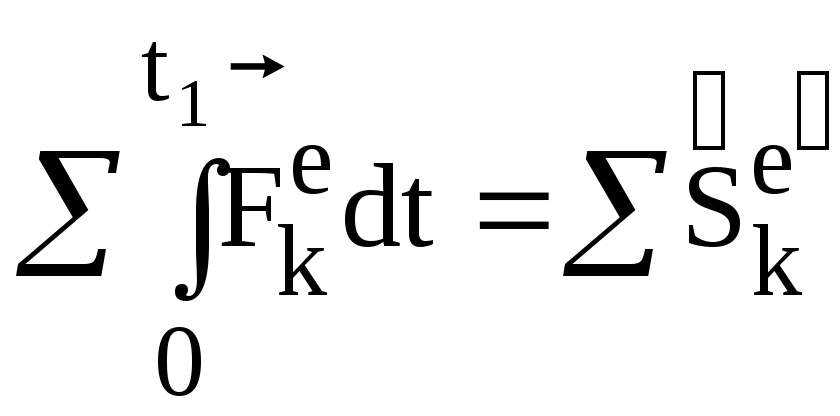 – импульсы
внешних сил.
В проекциях: Q1x
– Q0x
= Sekx.
Закон
сохранения количества движения:
– импульсы
внешних сил.
В проекциях: Q1x
– Q0x
= Sekx.
Закон
сохранения количества движения:
![]()
![]() =
const,
в проекциях:
=
const,
в проекциях:
![]()
Qx=
const.
Дифференциальное уравнение движения
точки переменной массы:
Qx=
const.
Дифференциальное уравнение движения
точки переменной массы:
![]() – уравнение
Мещерского,
– уравнение
Мещерского,
![]() – реактивная
сила,
– реактивная
сила,
![]() секундный расход топлива,
секундный расход топлива,
![]() .
Формула
Циолковского:
.
Формула
Циолковского:
![]() .
.
![]() – число Циолковского, m0
– стартовая масса ракеты.
Главный момент количеств движения
матер. системы (кинетический момент)
– число Циолковского, m0
– стартовая масса ракеты.
Главный момент количеств движения
матер. системы (кинетический момент)
![]() . Теорема об
изменении кинетического момента:
. Теорема об
изменении кинетического момента:
![]() ;
;
![]() .
Закон
сохранения кинетического момента:
если
.
Закон
сохранения кинетического момента:
если
![]() ,
то
,
то
![]() .
Кинетический момент вращающегося тела
Kz
= Jz.
Если Mz=
0, то Jz
= const.
Кинетическая
энергия системы
.
Кинетический момент вращающегося тела
Kz
= Jz.
Если Mz=
0, то Jz
= const.
Кинетическая
энергия системы
![]() .
.
Т
= Тк.
Поступательное движение: Тпост=![]() .
Вращательное: Твр=
.
Вращательное: Твр=![]() .
Плоскопараллельное (плоское): Тпл=
.
Плоскопараллельное (плоское): Тпл=![]() +
+![]() ,
vC
– скорость центра масс. Теорема Кенига:
Т=
,
vC
– скорость центра масс. Теорема Кенига:
Т=![]() +
+![]() .
Работа момента:
.
Работа момента:
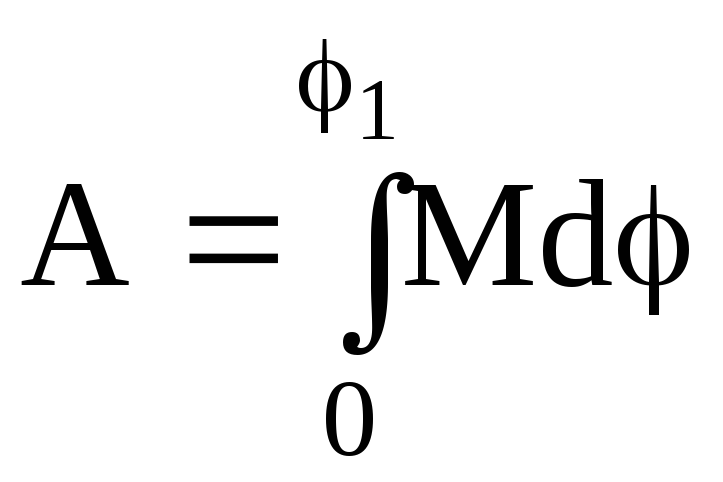 .
Мощность: N=Mz.
.
Мощность: N=Mz.
Теорема об изменении кинетической энергии системы: в дифференциальной форме:
dT
=
![]() ,
в конечной форме: Т2
– Т1=
,
в конечной форме: Т2
– Т1=
![]() .
Для неизменяемой системы
.
Для неизменяемой системы
![]() и Т2
– Т1=
и Т2
– Т1=
![]() .
Коэффициент полезного действия:
.
Коэффициент полезного действия:![]() ,
,
= Nмаш/Nдв. Закон сохранения полной механической энергии: Т + П = const.
Дифференциальные
уравнения поступательного движения
тела:
![]() и т.д.
и т.д.
Дифф-ные
уравнения вращения тела вокруг неподвижной
оси:
![]() ,
,
![]() .
.
1)
если
![]() =
0, то
= const; 2)
=
0, то
= const; 2)
![]() =
const, то
= const.
=
const, то
= const.
Уравнение
вращательного движения физического
маятника:
![]() ,
,
![]() ,
дифференциальное уравнение колебаний
маятника:
,
дифференциальное уравнение колебаний
маятника:
![]() ,
sin
,
,
sin
,
тогда
![]() – дифференциально уравнение гармонических
колебаний.
– дифференциально уравнение гармонических
колебаний.
Решение
этого уравнения:
= С1coskt
+ C2
sinkt
или
= sin(kt
+ ).
Период малых колебаний физического
маятника Т= 2/k
= 2![]() .
Для математического
маятника:
.
Для математического
маятника:![]() ,
L=
,
L=![]() –
приведенная длина физического маятника.
–
приведенная длина физического маятника.
Дифф.
урав-ния плоского движения тела:
![]() ;
;
![]() ;
;
![]() .
.
![]() — принцип
Даламбера
для материальной точки.
— принцип
Даламбера
для материальной точки.
Сила
инерции:
![]() ,
знак (–) означает, что сила инерции
против ускорения.
,
знак (–) означает, что сила инерции
против ускорения.
Для
системы добавляется уравнение:
![]() .
.
![]() – главный
вектор сил инерции,
– главный
вектор сил инерции,
![]() – главный момент сил инерции.
– главный момент сил инерции.
![]() ,
,
![]() — уравнения кинетостатики.
— уравнения кинетостатики.
Главный
вектор сил инерции
![]() .
Главный момент сил инерции при плоском
движении:
.
Главный момент сил инерции при плоском
движении:
![]() ,
при вращении вокруг оси z:
,
при вращении вокруг оси z:
![]() .
.
Определение реакций при вращении твердого тела вокруг неподвижной оси.
Центробежная
сила инерции
![]()
![]() ,
вращательная
,
вращательная
![]() .
.
![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() –
центробежные моменты инерции,
–
центробежные моменты инерции,
![]() .
.
Уравнения равновесия кинетостатики:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Условия отсутствия динамических составляющих:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
откуда xC= 0, yC= 0, Jyz= 0, Jzx= 0.
Основы аналитической механики
Принцип возможных перемещений:
![]() ;
;
![]() .
.
Общее
уравнение динамики
![]() .
.
Уравнения
Лагранжа 2-го рода:
![]() ,
(i=1,2…s),
s
– число степеней свободы; qi
– обобщенная координата;
,
(i=1,2…s),
s
– число степеней свободы; qi
– обобщенная координата;
![]() –
обобщенная скорость,
–
обобщенная скорость,
Т
= Т(q1,q2,…,qS,![]() ,
,![]() …
…![]() ,t)
– кинетическая энергия; Qi
– обобщенная сила.
,t)
– кинетическая энергия; Qi
– обобщенная сила.
![]() .
.
![]() ,
П = П(q1,q2,…,qS,t)
– потенциальная энергия.
,
П = П(q1,q2,…,qS,t)
– потенциальная энергия.
Функция
Лагранжа:
L
= T
– П,
![]() – уравнения Лагранжа второго рода для
консервативной системы.
– уравнения Лагранжа второго рода для
консервативной системы.
При
стационарных связях
![]() – квадратичная форма обобщенных
скоростей, aij=
aji
– коэффициенты
инерции.
– квадратичная форма обобщенных
скоростей, aij=
aji
– коэффициенты
инерции.
