
Статика
Равнодействующая
двух пересекающихся сил–
![]() ;
диагональ параллелограмма
;
диагональ параллелограмма
![]() .
Равнодействующая сходящихся сил
.
Равнодействующая сходящихся сил
![]() .
Проекции
силы на оси координат
(для плоской системы сил): Fx=Fcos;
Fy=Fcos.
Модуль
силы:
.
Проекции
силы на оси координат
(для плоской системы сил): Fx=Fcos;
Fy=Fcos.
Модуль
силы:![]()
![]() ;
направляющие
косинусы:
;
направляющие
косинусы:
![]() разложение на составляющие:
разложение на составляющие:
![]() ,
Для пространственной системы:
,
Для пространственной системы:
![]() ,
,
Fx=Fcos;
Fy=Fcos;
Fz=Fcos;
![]() ;
;
![]() .
.
Проекции
равнодействующей системы сходящихся
сил на координатные оси: Rx=Fix;
Ry=Fiy;
Rz=Fiz;
![]() .
Условия
равновесия сист. сходящихся сил:
геометрическое:
.
Условия
равновесия сист. сходящихся сил:
геометрическое:![]() ,
аналитические: Fix=0;
Fiy=0;
Fiz=0.
Условие
равновесия пар сил:
,
аналитические: Fix=0;
Fiy=0;
Fiz=0.
Условие
равновесия пар сил:
![]() .
Момент силы
относительно точки:
.
Момент силы
относительно точки:![]()
![]() – векторное произведение. Модуль
векторного произведения:
– векторное произведение. Модуль
векторного произведения:
![]() RFsin=
Fh.
Плоская система сил:
RFsin=
Fh.
Плоская система сил:
![]() Fh,
>0 – против час.стр.; <0 – по час.стр.
Fh,
>0 – против час.стр.; <0 – по час.стр.
 =(yFz
– zFy)
=(yFz
– zFy)![]() +(zFx
– xFz)
+(zFx
– xFz)![]() +(xFy
– yFx)
+(xFy
– yFx)![]() ,
проекции момента силы на оси координат:
М0x(
,
проекции момента силы на оси координат:
М0x(![]() )=yFz
– zFy;
М0y(
)=yFz
– zFy;
М0y(![]() )=zFx
– xFz;
М0z(
)=zFx
– xFz;
М0z(![]() )=xFy
– yFx.
)=xFy
– yFx.
Условия равновесия
пл. сист. сил:
аналитич.:![]() ,
или
,
или![]() ,
А,В,С – точки не на одной прямой, или
,
А,В,С – точки не на одной прямой, или
![]() ,
ось "х" не перпендикулярна отрезку
АВ.
,
ось "х" не перпендикулярна отрезку
АВ.
Закон
Кулона (закон
Амонта – Кулона):
![]() .
Сила трения скольжения:
.
Сила трения скольжения:
![]() .
tgсц=fсц;
tgтр=f.
Мтр=
fkN
– момент трения качения. Момент силы
относительно оси:
.
tgсц=fсц;
tgтр=f.
Мтр=
fkN
– момент трения качения. Момент силы
относительно оси:
![]() .
Моменты силы относительно осей координат:
Мx(
.
Моменты силы относительно осей координат:
Мx(![]() )=yFz
– zFy;
Мy(
)=yFz
– zFy;
Мy(![]() )=zFx
– xFz;
Мz(
)=zFx
– xFz;
Мz(![]() )=xFy
– yFx.
Статические инварианты: 1-ый – квадрат
модуля главного вектора: I1=
Fo2=
Fx2+Fy2+Fz2;
2-ой – скалярное произв. главного вектора
на гл. момент: I2=
)=xFy
– yFx.
Статические инварианты: 1-ый – квадрат
модуля главного вектора: I1=
Fo2=
Fx2+Fy2+Fz2;
2-ой – скалярное произв. главного вектора
на гл. момент: I2=
![]() =FxMx+FyMy+FzMz.
=FxMx+FyMy+FzMz.
Проекция
гл. момента на направление гл. вектора
![]() .
Мmin=M*
.
Мmin=M*
Главный
вектор
![]() и главный момент
и главный момент
![]() ,
,
уравнения
центральной оси:
![]() .
.
Условия
равновесия простр. сист.сил:
Fkx=0;
Fky=0;
Fkz=0;
Mx(Fk)=0;
My(Fk)=0;
Mz(Fk)=0.
Условия
равновесия для системы параллельных
сил (||z):
Fkz=0;
Mx(Fk)=0;
My(Fk)=0.
Координаты центра ||-ых сил:
![]() .
Координаты центра тяжести:
.
Координаты центра тяжести:
![]() ;
;
![]() ;
где Р=рk.
Центр тяжести плоской фигуры:
;
где Р=рk.
Центр тяжести плоской фигуры:
![]() ,
,
![]() .
Центр тяжести: дуги окружности с
центральным углом 2:
.
Центр тяжести: дуги окружности с
центральным углом 2:
![]() ;
кругового сектора:
;
кругового сектора:
![]() .
.
Статический момент площади плоской фигуры – Sx=yiFi= Fyc; Sy=xiFi= Fxc.
Объем тела вращения V=2xcF; площадь поверхности вращения F=2xcL.
Центр
тяжести плоской фигуры с вырезанной
частью:
![]() .
.
Кинематика
s=f(t) –естественный способ задания движения, прямолинейное движение: х=f(t).
Координатный способ: x=f1(t), y=f2(t), z=f3(t). Уравнение траектории: f(x,y,z)=0.
Векторный
способ:
радиус-вектор
![]() =
=![]() ,
модуль
,
модуль
![]() ,
направляющие косинусы:
,
направляющие косинусы:
![]() и т.д. Переход от координатного способа
к естественному:
и т.д. Переход от координатного способа
к естественному:
![]() .
Скорость
точки. Вектор
скорости:
.
Скорость
точки. Вектор
скорости:
![]() ;
;
![]() .
Проекции скорости:
.
Проекции скорости:
![]() ,
,
![]() ,
,
![]() .
Модуль скорости:
.
Модуль скорости:
![]() ,
направляющие косинусы:
,
направляющие косинусы:
![]() и т.д.
и т.д.
Естественный
способ:
![]() ,
,
![]() ,
,
![]() –
орт касательной. Движение в полярной
системе координат: r=r(t)
– полярный радиус, =(t)
– угол. Проекции скорости на радиальное
направление
–
орт касательной. Движение в полярной
системе координат: r=r(t)
– полярный радиус, =(t)
– угол. Проекции скорости на радиальное
направление
![]() ,
поперечное направление
,
поперечное направление
![]() ,
модуль скорости
,
модуль скорости
![]() .;
x=rcos,
y=rsin.
Ускорение
точки.
.;
x=rcos,
y=rsin.
Ускорение
точки.
![]() .
Проекции уск.-я:
.
Проекции уск.-я:
![]() и т.д. Модуль уск.-я:
и т.д. Модуль уск.-я:![]() ,
направляющ. косинусы:
,
направляющ. косинусы:
![]() ,
и т.д. Проекции уск. на радиальное напр-ние
,
и т.д. Проекции уск. на радиальное напр-ние
![]() ,
поперечное напр-ние
,
поперечное напр-ние
![]() ,
модуль уск-я
,
модуль уск-я
![]() .
.
![]() .
Модуль нормального ускорения:
.
Модуль нормального ускорения:
![]() ,
– радиус кривизны траектории, модуль
касательного ускорения
,
– радиус кривизны траектории, модуль
касательного ускорения
![]() ,
,
![]()
![]() ,
,
![]() .
Прямолинейное движение: =
,
аn=0,
a=a.
Равномерное криволинейное движение:
v=const,
a=0,
a=an.
s=s0+vt,
при s0=0
v=s/t.
Равномерное прямолинейное движение:
а=a=an=0.
.
Прямолинейное движение: =
,
аn=0,
a=a.
Равномерное криволинейное движение:
v=const,
a=0,
a=an.
s=s0+vt,
при s0=0
v=s/t.
Равномерное прямолинейное движение:
а=a=an=0.
4)
Равнопеременное криволинейное движение:
a=const,
v=v0+at,
![]() .
.
Угловая
скорость:
![]() ,
,
![]() .
Угловое
ускорение
тела:
.
Угловое
ускорение
тела:
![]() .
Равномерное вращение: =const,
=t,
=/t,
равнопеременное вращение: =0+t;
.
Равномерное вращение: =const,
=t,
=/t,
равнопеременное вращение: =0+t;
![]() .
Скорости и ускорения точек вращающегося
тела:
.
Скорости и ускорения точек вращающегося
тела:
![]() .
.
v=rsin() = (CM), (СМ) – расстояние от точки М до оси вращения.
Формулы
Эйлера:
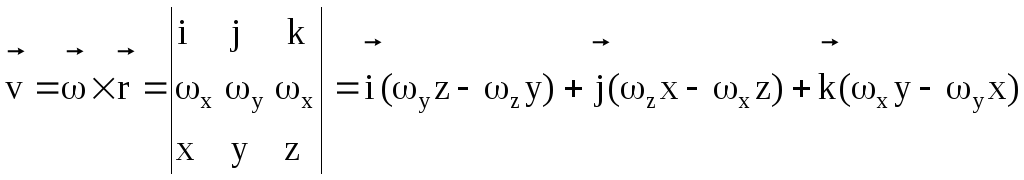 ,
,
vx=yz
– zy;
vy=zx
– xz;
vz=xy
– yx.
Если ось вращения совпадает с осью z,
то vx=
– y;
vy=x.
Ускорение:
![]() .
Вращательное уск.
.
Вращательное уск.
![]() ,
авр=rsin,
центростремительное уск.
,
авр=rsin,
центростремительное уск.
![]() ,
ац=2R.
Полное ускорение:
,
ац=2R.
Полное ускорение:
![]() .
Угол, между полным и центростремительным
ускорениями:
.
Угол, между полным и центростремительным
ускорениями:
![]() .
Плоское
движение твердого тела.
.
Плоское
движение твердого тела.
Уравнения
плоского движения:
xA=
f1(t),
yA=
f2(t),
= f3(t),
Скорость
![]() ;
;
![]() ,
vBA=
BA,
vAcos
= vBcos.
Мгновенный
центр ск-ей
– Р:
,
vBA=
BA,
vAcos
= vBcos.
Мгновенный
центр ск-ей
– Р:
![]() .
.
![]() ,
,
![]() .
Ускорения:
.
Ускорения:
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
 ,
,
![]() .
Мгновенный центр
уск-ий – Q;
.
Мгновенный центр
уск-ий – Q;
![]() ,
,
![]() ,
,
![]() .
Сферическое
движение твердого тела.
Уравнения сферического движения:
=f1(t);
=f2(t);
=f3(t)
– угол прецессии,
– угол нутации,
– угол собственного вращения — углы
Эйлера. Угловое ускорение:
.
Сферическое
движение твердого тела.
Уравнения сферического движения:
=f1(t);
=f2(t);
=f3(t)
– угол прецессии,
– угол нутации,
– угол собственного вращения — углы
Эйлера. Угловое ускорение:
![]() .
Скорости точек при сферич. движ.:
.
Скорости точек при сферич. движ.:
![]() ,
модуль v=rsin=h,
h–
расстояние от точки до мгновенной оси
вращения.
,
модуль v=rsin=h,
h–
расстояние от точки до мгновенной оси
вращения.
Формулы
Эйлера:
 .
.
Ускорения:
![]() ,
вращательное ускорение
,
вращательное ускорение
![]() модуль вращат. уск. авр=rsin=h1,
h1–
расст. от точки до вектора
модуль вращат. уск. авр=rsin=h1,
h1–
расст. от точки до вектора
![]() ,
осестремительное ускорение
,
осестремительное ускорение
![]() ,
аос=2h.
Движение
свободного тв.тела. Ур-ия
движ.св.тв.тела: xA=f1(t);
yA=f2(t);
zA=f3(t);
=f4(t);
=f5(t);
=f6(t)
(углы Эйлера). Скорость точки св.тв.тела:
,
аос=2h.
Движение
свободного тв.тела. Ур-ия
движ.св.тв.тела: xA=f1(t);
yA=f2(t);
zA=f3(t);
=f4(t);
=f5(t);
=f6(t)
(углы Эйлера). Скорость точки св.тв.тела:
![]() .
Ускорение точки св.тв. тела:
.
Ускорение точки св.тв. тела:
![]() .
.
Сложное движение точки. Теорема о сложении скоростей:
![]() ,
,
![]() ;
;
![]()
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
