
Курсовая работа - Статика, кинематика, динамика двухступенчатого манипулятора. Вариант 131 / !!!!!!мой курсач 13 вариант) наконец таки готов!)
.docxФедеральное агентство по образованию
Государственное общеобразовательное учреждение
Высшего профессионального образования
Уфимский государственный авиационный технический университет
Кафедра теоретической механики
/*печать: 11стр.*/
Курсовая работа по теоретической механике
«Статика, кинематика, динамика двухступенчатого манипулятора»
Вариант №13
Выполнил: студент гр. РС-218
Шикунов В.В.
Проверил: профессор кафедры ТМ
Ковган С.Т.
Уфа 2008
Цель курсовой работы:
-
Статика. Определить реакции и моменты относительно осей в точке О, путем рассмотрения манипулятора целиком, и по частям.
-
Кинематика. Записать координаты центров тяжести стержней С1, С2, С3, через алгебраические суммы проекций известных отрезков. Определить проекции векторов скорости и ускорения точки D(захват) на оси координат, затем найти полную скорость и ускорение точки D. Продифференцировать по времени два раза законы изменения координат центров тяжести стержней С1, С2, С3. Изобразить векторы скоростей и ускорений центров масс манипулятора Определить скорость и ускорение точки D методами кинематики сложного движения точки. Сравнить полученные значения скоростей и ускорений для точки D.
-
Динамика. Определить главные вектора сил инерции, прикладываемых к каждому прямолинейному участку звеньев манипулятора. Определить главные моменты сил инерции, приведенных к центрам масс каждого прямолинейного участка манипулятора. Изобразить силы инерции и моменты сил инерции, действующие на каждое тело. Составить уравнения условного равновесия по принципу Даламбера. Выразить кинетическую энергию в функции обобщенных координат q1, q2.
Т.е.
Т=Т(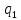 ,
,
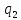 ,
,
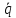 1,
1,
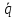 2).
Составить уравнения Лагранжа II
рода для определения управляющих сил
и управляющих моментов. Построить
графики их изменения в функции от
времени.
2).
Составить уравнения Лагранжа II
рода для определения управляющих сил
и управляющих моментов. Построить
графики их изменения в функции от
времени.
Раздел I. Статика
На
рисунке представлен манипулятор в
исходном положении.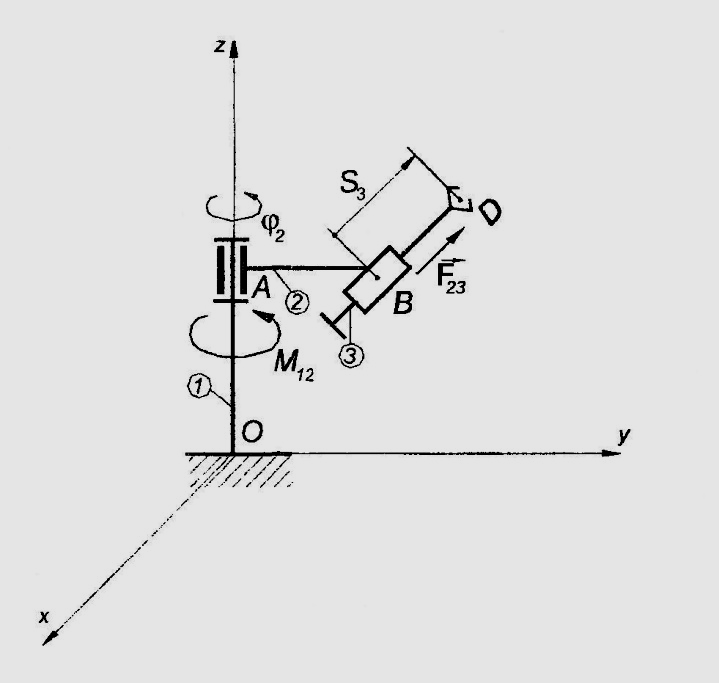
Манипулятор состоит из трех частей:
-
Неподвижной стойки
-
Кронштейн, вращающийся относительно оси стойки по закону: φ2=-t2+2t, рад.
-
Рука, поступательно перемещающаяся относительно кронштейна по закону: S3=0,2t+0,15t2,м.
Основные характеристики манипулятора:
l1=0,8м.; P1=40Н;
l2=0,8м.; P2=40Н;
l3=0,6м.; P3=30Н;
Координаты точки D изменяются во времени по законам:
XD=-0,8∙sin(-t2+2t)+( 0,2t+0,15t2)∙cos∙(-t2+2t), м.
YD=0,8∙cos(-t2+2t)+( 0,2t+0,15t2)∙sin∙(-t2+2t), м.
ZD=0,8, м.
Рис 1. Манипулятор в исходном положении
В момент времени t=1c. кронштейн AB повернется вокруг оси Z на угол φ2=1рад., рука BD выдвинется на длину S3=0,35 м., точка D будет иметь следующие координаты:
XD= -0,484м. ; YD= 0,727м. ; ZD=0,8м.
На точку D действуют силы: Fx=F1=5Н, Fy=F2=-4Н, Fz=F3=4Н.
Рассмотрим равновесие манипулятора целиком:
∑X=0; Xo+Fx=0; Xo =-Fx=-5Н;
∑У=0; Yo+Fу=0; Yo =-Fy=4Н;
∑Z=0; Zo- P1-P2-P3+Fz =0; Zo=P1+P2+P3-Fz=106H
∑mx(F)=0; Mxo-Fy∙ZD+Fz∙YD-0,5∙P2∙l2∙cosφ2-P3∙(l2∙cosφ2-(S3-0,5∙l3) sinφ2)=0
Mxo=Fy∙ZD-Fz∙YD+0,5∙P2∙l2∙cosφ2+P3∙(l2∙cosφ2-(S3-0,5∙l3) sinφ2)=
=-4∙0,8-4∙0,727+0,5∙40∙0,8∙0,54+30(0,8∙0,54-0,05∙0,84)=5,24H∙м.
∑my(F)=0; Myo+Fx∙ZD+Fz∙XD-0,5∙P2∙l2∙sinφ2-P3∙(l2∙sinφ2-(S3-0,5∙l3) cosφ2)=0
Myo=-Fx∙ZD-Fz∙XD+0,5∙P2∙l2∙sinφ2+P3∙(l2∙sinφ2-(S3-0,5∙l3) cosφ2)=
=-5∙0,8-4∙0,484+0,5∙40∙0,8∙0,84+30∙(0,8∙0,84-0,05∙0,54)=27,02H∙м.
∑mz(F)=0; Mzo=-Fx∙YD-Fy∙XD=-5∙0,727-4∙0,484=-2,76 Н м.
Теперь рассмотрим равновесие руки манипулятора, считая реакции в точке В неизвестными.
∑X=0; 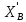 =-FX=-5H.
=-FX=-5H.
∑У=0; 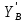 =-FY=4H.
=-FY=4H.
∑Z=0; 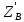 =P3-Fz=26H.
=P3-Fz=26H.
∑mx(F)=0;
 +P3∙(
S3-0,5∙l3)
sinφ2+FZ∙S3∙sinφ2=0
+P3∙(
S3-0,5∙l3)
sinφ2+FZ∙S3∙sinφ2=0
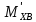 =-P3∙(S3-0,5∙l3)
sinφ2-FZ∙S3∙sinφ2=
=-P3∙(S3-0,5∙l3)
sinφ2-FZ∙S3∙sinφ2=
=-30∙(0,35-0,5∙0,6)∙0,84-4∙0,35∙0,84=11,44H м.
∑my(F)=0;
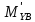 -P3∙(
S3-0,5∙l3)
cosφ2+FZ∙S3∙cosφ2=0
-P3∙(
S3-0,5∙l3)
cosφ2+FZ∙S3∙cosφ2=0
 =P3∙(
S3-0,5∙l3)
cosφ2-FZ∙S3∙cosφ2=
=P3∙(
S3-0,5∙l3)
cosφ2-FZ∙S3∙cosφ2=
=30∙(0,35-0,5∙0,6)∙0,54-4∙0,35∙0,54=-0,05H м.
∑mz(F)=0;
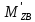 +FX∙S3∙sinφ2-
FY∙S3∙cosφ2=0
+FX∙S3∙sinφ2-
FY∙S3∙cosφ2=0
 =FY∙S3∙cosφ2-
FX∙S3∙sinφ2=
=FY∙S3∙cosφ2-
FX∙S3∙sinφ2=
=-4∙0,35∙0,54-5∙0,35∙0,84=-2,22H м.
Рассмотрим равновесие кронштейна, считая реакции в точке A неизвестными.
 =-
=-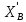 =5H.
=5H.  =-
=-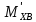 =11,44H
м.
=11,44H
м.
 =-
=-
 =-4H.
=-4H.  =-
=- =0,05H
м.
=0,05H
м.
 =-
=-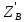 =-26H.
=-26H.  =-
=- =2,22H
м.
=2,22H
м.
∑X=0;  =-
=-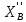 =-5H.
=-5H.
∑У=0;  =-
=-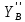 =4H.
=4H.
∑Z=0;  =-
=-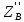 +P2=66H.
+P2=66H.
∑mx(F)=0;
 +
+ -0,5∙P2∙l2∙cosφ2+
-0,5∙P2∙l2∙cosφ2+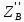 ∙l2∙cosφ2=0
∙l2∙cosφ2=0
 +0,5∙P2∙l2∙cosφ2-
+0,5∙P2∙l2∙cosφ2- ∙l2∙cosφ2=
∙l2∙cosφ2=
=-11,44+0,5∙40∙0,8∙0,54-(-26)∙0,8∙0,54 =8,44H м.
∑my(F)=0;
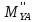 +
+ -0,5∙P2∙l2∙sinφ2+
-0,5∙P2∙l2∙sinφ2+ ∙l2∙sinφ2=0
∙l2∙sinφ2=0
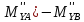 +0,5∙P2∙l2∙sinφ2-
+0,5∙P2∙l2∙sinφ2- ∙l2∙sinφ2=
∙l2∙sinφ2=
=-0,05∙40∙0,8∙0,84-(-26)∙0,8∙0,84=31,02H м.
∑mz(F)=0;
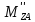 +
+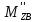 -
-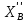 ∙l2∙cosφ2-
∙l2∙cosφ2-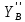 ∙l2∙
=0
∙l2∙
=0
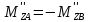 +
+ ∙l2∙cosφ2+
∙l2∙cosφ2+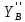 ∙l2∙
sinφ2=
∙l2∙
sinφ2=
=-2,22+5∙0,8∙0,54+(-4)∙0,8 ∙0,84=-2,75H м.
Рассмотрим равновесие стойки манипулятора, считая реакции в точке О неизвестными.
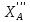 =-
=-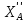 =5H.
=5H.  =-
=-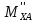 =-8,44H
м.
=-8,44H
м.
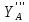 =-
=-
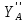 =-4H.
=-4H. 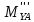 =-
=-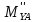 =-31,02H
м.
=-31,02H
м.
 =-
=- =-66H.
=-66H. 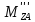 =-
=-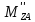 =2,75H
м.
=2,75H
м.
∑X=0; 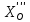 =-
=- =-5H.
=-5H.
∑У=0;  =-
=-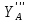 =4H.
=4H.
∑Z=0; 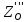 =P1-
=P1- =106H.
=106H.
∑mx(F)=0; 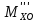 +
+ -
-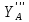 ∙l1=0
∙l1=0
 =-
=-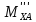 +
+ ∙l1=8,44+(-4)∙0,8=5,24H
м.
∙l1=8,44+(-4)∙0,8=5,24H
м.
∑my(F)=0;  +
+ +
+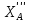 ∙l1=0
∙l1=0
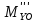 =-
=- -
-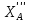 ∙l1=31,02-5∙0,8=27,02H
м.
∙l1=31,02-5∙0,8=27,02H
м.
∑mz(F)=0;  +
+ =0
=0
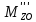 =-
=-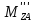 =-2,76H
м.
=-2,76H
м.
Раздел II Кинематика.
Длины звеньев манипулятора:
l1=0,8м.;
l2=0,8м.;
l3=0,6м.;
Законы движения звеньев:
φ2=-t2+2t, рад.
S3=0,2t+0,15t2, м.
Уравнение изменения координат точки D в функции от времени:
XD=-0,8sin(-t2+2t)-( 0,2t+0,15t2)∙cos(-t2+2t), м.
YD=0,8∙cos∙(-t2+2t)+( 0,2t+0,15t2)∙sin∙(-t2+2t), м.
ZD=0,8, м.
Уравнение изменения координат точки С2(центра тяжести кронштейна) в функции от времени:
XС2=-0,8∙0.5∙sin(-t2+2t), м.
YС2=0,8∙0,5∙cos(-t2+2t), м.
ZС2=0,8, м.
Уравнение изменения координат точки С3(центра тяжести руки) в функции от времени:
XС3=-0,8∙0.5∙sin(-t2+2t)- (( 0,2t+0,15t2)-0,3)∙cos(-t2+2t), м.
YС3=0,8∙0,5∙cos(-t2+2t)- (( 0,2t+0,15t2)-0,3)∙sin(-t2+2t), м.
ZС3=0,8, м.
Определим проекции вектора скорости захвата на оси координат:
 D=-0,8∙cos(-t2+2t)∙(-2t+2)+(0,2t+0,15t2)∙sin(-t2+2t)∙(-2t+2)-(0,2+0,3t)∙cos(-t2+2t)=
D=-0,8∙cos(-t2+2t)∙(-2t+2)+(0,2t+0,15t2)∙sin(-t2+2t)∙(-2t+2)-(0,2+0,3t)∙cos(-t2+2t)=
=-0,8∙0,54∙0+0,35∙0,84∙0-0,5∙0,54=0,27 м/с.
 D=-0,8∙sin(-t2+2t)∙(-2t+2)+(0,2t+0,15t2)∙cos(-t2+2t)∙(-2t+2)+(0,2+0,3t)∙sin(-t2+2t)=
D=-0,8∙sin(-t2+2t)∙(-2t+2)+(0,2t+0,15t2)∙cos(-t2+2t)∙(-2t+2)+(0,2+0,3t)∙sin(-t2+2t)=
=-0,8∙0,84∙0+0,35∙0,54∙0+0,5∙0,84=0,42 м/с.
 D=0
м/с.
D=0
м/с.
Найдем полную скорость захвата VD:
VD=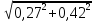 =0,5м/с.
=0,5м/с.
Определим проекции вектора ускорения захвата на оси координат:
 D=[2∙0,8∙cos(-t2+2t)
(-2t+2)+0,8
sin(-t2+2t)∙(-2t+2)
(-2t+2)]+[-(0,3t3-0,1t2+0,4t)
cos(-t2+2t)
(-2t+2)+
D=[2∙0,8∙cos(-t2+2t)
(-2t+2)+0,8
sin(-t2+2t)∙(-2t+2)
(-2t+2)]+[-(0,3t3-0,1t2+0,4t)
cos(-t2+2t)
(-2t+2)+
+(0,9t2-0,2t+0,4)∙sin(-t2+2t)]-[0,3∙cos(-t2+2t)+(0,2+0,3t)sin(-t2+2t)∙(-2t+2)]=
=1,1∙0,84-0,3∙0,54=1,086м/с2.
 D=[2∙0,8∙sin(-t2+2t)
(-2t+2)+0,8∙cos(-t2+2t)∙(-2t+2)
(-2t+2)]+[(0,3t3-0,1t2+0,4t)
(-sin(-t2+2t)
(-2t+2))+
D=[2∙0,8∙sin(-t2+2t)
(-2t+2)+0,8∙cos(-t2+2t)∙(-2t+2)
(-2t+2)]+[(0,3t3-0,1t2+0,4t)
(-sin(-t2+2t)
(-2t+2))+
+(0,9t2-0,2t+0,4)∙cos(-t2+2t)]+[0,3∙sin(-t2+2t)+(0,2+0,3t)∙cos(-t2+2t)∙(-2t+2)]=
=1,1∙0,54+0,3∙0,84=0,846м/с2.
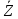 D=0
D=0
Найдем полное ускорение захвата WD:
WD=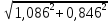 =1,37м/с2.
=1,37м/с2.
Продифференцируем во времени законы изменения координат точек С2 и С3:
Для точки С2:
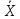 С2=-0,4∙cos(-t2+2t)∙(-2t+2)
м/с2.
С2=-0,4∙cos(-t2+2t)∙(-2t+2)
м/с2.
 С2=-0,4∙sin(-t2+2t)∙(-2t+2)
м/с2.
С2=-0,4∙sin(-t2+2t)∙(-2t+2)
м/с2.
 C2=0
м/с2.
C2=0
м/с2.
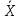 C2=-0,4∙cos(-t2+2t)∙(-2)+0,4∙sin(-t2+2t)∙(-2t+2)∙(-2t+2))
м/с2.
C2=-0,4∙cos(-t2+2t)∙(-2)+0,4∙sin(-t2+2t)∙(-2t+2)∙(-2t+2))
м/с2.
В
момент времени t=1c.: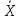 C2=0,43
м/с2.
C2=0,43
м/с2.
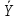 C2=-0,4∙sin(-t2+2t)∙(-2)-0,4∙cos(-t2+2t)∙(-2t+2)∙(-2t+2)
м/с2.
C2=-0,4∙sin(-t2+2t)∙(-2)-0,4∙cos(-t2+2t)∙(-2t+2)∙(-2t+2)
м/с2.
В
момент времени t=1c.: C2=0,67
м/с2.
C2=0,67
м/с2.
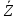 C2=0
м/с2.
C2=0
м/с2.
Для точки С3:
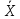 С3=-0,8∙cos(-t2+2t)∙(-2t+2)+(
0,2t+0,15t2)∙sin(-t2+2t)∙(-2t+2)м/с2.
С3=-0,8∙cos(-t2+2t)∙(-2t+2)+(
0,2t+0,15t2)∙sin(-t2+2t)∙(-2t+2)м/с2.
 С3=-0,8∙sin(-t2+2t)∙(-2t+2)-(
0,2t+0,15t2)∙cos(-t2+2t)∙(-2t+2)м/с2.
С3=-0,8∙sin(-t2+2t)∙(-2t+2)-(
0,2t+0,15t2)∙cos(-t2+2t)∙(-2t+2)м/с2.
 C3=0
м/с2.
C3=0
м/с2.
 C3=-0,8∙(-2)∙cos(-t2+2t)+0,8∙sin(-t2+2t)∙(-2t+2)∙(-2t+2)+
C3=-0,8∙(-2)∙cos(-t2+2t)+0,8∙sin(-t2+2t)∙(-2t+2)∙(-2t+2)+
+(-0,9t2-0,2t+0,4) sin(-t2+2t)+(-0,3t3-0,1t2+0,4t) cos(-t2+2t)∙(-2t+2) м/с2.
В
момент времени t=1c.:
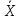 C3
=0,28
м/с2.
C3
=0,28
м/с2.
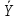 C3=-0,8∙(-2)∙sin(-t2+2t)-0,8∙cos(-t2+2t)∙(-2t+2)∙(-2t+2)+
C3=-0,8∙(-2)∙sin(-t2+2t)-0,8∙cos(-t2+2t)∙(-2t+2)∙(-2t+2)+
+(-0,9t2-0,2t+0,4) cos(-t2+2t)-(-0,3t3-0,1t2+0,4t) sin(-t2+2t)∙(-2t+2) м/с2.
В
момент времени t=1c.: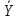 C3=
0,97м/с2.
C3=
0,97м/с2.
 C3=0м/с2.
C3=0м/с2.
Определим скорость и ускорение точки В методом кинематики сложного движения точки.
За
переносное движение примем вращательное
движение кронштейна(ωe= ),
а за относительное – поступательное
движение руки манипулятора(vr=
),
а за относительное – поступательное
движение руки манипулятора(vr= ).
).
ωe=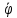 =0рад/с;
=0рад/с;
vr= =0,5м/с.
=0,5м/с.
Определим скорость точки D:
va=ve+vr
ve=ωe∙l2=0м/с;
vr= =0,5
м/с, отсюда
абсолютная скорость точки D
равна:
=0,5
м/с, отсюда
абсолютная скорость точки D
равна:
va=0,5 м/с;
Определим ускорение точки D:
 =
=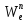 +
+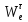 +
+ +
+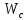
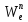 =
=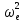 ∙l2=0м/с2.
∙l2=0м/с2.
 =ε∙l2=-1,6м/с2.
=ε∙l2=-1,6м/с2.
 =
= =0,3м/с2.
=0,3м/с2.
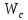 =2ωe
=2ωe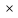 vr=0м/с2.
vr=0м/с2.
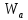 =-1,6+0,3=-1,3м/с2.
=-1,6+0,3=-1,3м/с2.
Раздел III Динамика.
В этом разделе необходимо провести динамический расчет манипулятора – найти управляющий момент в точке А и управляющую силу в точке В двумя способами: используя уравнения условного равновесия тела и применяя уравнения Лагранжа II рода. Сделать вывод о верности решения и построить графики зависимости управляющего момента и управляющей силы от времени. Исходные данные представлены на рис.8.
В предыдущем разделе были найдены ускорения центров масс частей манипулятора:
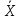 C1=0
м/с2.
C1=0
м/с2.
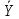 C1=0
м/с2.
C1=0
м/с2.
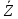 C1=0
м/с2.
C1=0
м/с2.
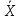 C2=-0,4∙cos(-t2+2t)∙(-2)+0,4∙sin(-t2+2t)∙(-2t+2)∙(-2t+2)
м/с2.
C2=-0,4∙cos(-t2+2t)∙(-2)+0,4∙sin(-t2+2t)∙(-2t+2)∙(-2t+2)
м/с2.
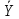 C2=-0,4∙sin(-t2+2t)∙(-2)-0,4∙cos(-t2+2t)∙(-2t+2)∙(-2t+2)
м/с2.
C2=-0,4∙sin(-t2+2t)∙(-2)-0,4∙cos(-t2+2t)∙(-2t+2)∙(-2t+2)
м/с2.
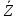 C2=0
м/с2.
C2=0
м/с2.
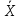 C3=-0,8∙(-2)∙cos(-t2+2t)+0,8∙sin(-t2+2t)∙(-2t+2)∙(-2t+2)+
C3=-0,8∙(-2)∙cos(-t2+2t)+0,8∙sin(-t2+2t)∙(-2t+2)∙(-2t+2)+
+(-0,9t2-0,2t+0,4) sin(-t2+2t)+(-0,3t3-0,1t2+0,4t) cos(-t2+2t)∙(-2t+2) м/с2.
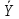 C3=-0,8∙(-2)∙sin(-t2+2t)-0,8∙cos(-t2+2t)∙(-2t+2)∙(-2t+2)+
C3=-0,8∙(-2)∙sin(-t2+2t)-0,8∙cos(-t2+2t)∙(-2t+2)∙(-2t+2)+
+(-0,9t2-0,2t+0,4) cos(-t2+2t)-(-0,3t3-0,1t2+0,4t) sin(-t2+2t)∙(-2t+2) м/с2.
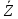 C3=0м/с2.
C3=0м/с2.
Обозначим все динамические силы, действующие на манипулятор (рис.9):
На центр масс руки (точка С3) действуют силы инерции:
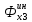 =-m3∙
=-m3∙ C3
C3
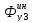 =-m3
=-m3 C3
C3
 =-m3∙
=-m3∙ C3=0
C3=0
Так как рука (3) движется поступательно относительно кронштейна (2), то моментов инерции е будет.
На центр масс кронштейна (точка С2) действуют силы инерции:
 =-m2∙
=-m2∙ C2
C2
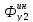 =-m2∙
=-m2∙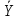 C2
C2
 =-m2∙
=-m2∙ C2=0
C2=0
И моменты инерции:
 =-
=- +(
+( )
) =0
=0
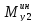 =-
=-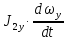 +(
+(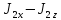 )
)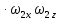 =0
=0
 =-
=- +(
+( )
)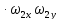 =-
=-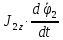 =-
=-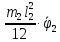 ;
мы
учли, что
;
мы
учли, что
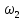 =(0,0,
=(0,0,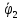 ),
),
т.е.
 .
.
Рассмотрим отдельно руку (3) и запишем уравнения её условного равновесия (рис.10), совместив начало координат с точкой B.
∑X=0;  +
+ +
+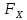 =0;
=0;
 =-
=-
∑У=0;  +
+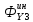 +
+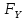 =0;
=0;
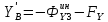
∑Z=0; 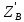 +
+ -
- =0;
=0;
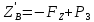
∑mx(F)=0;  -
-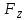 ∙
∙ ∙
sinφ2+
∙
sinφ2+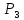 (
( )∙sinφ2=0;
)∙sinφ2=0;
