3 Практична частина

3.1 Контрольний приклад

За даними лабораторних досліджень електричний струм (mkA), якій протікає по рослині протягом доби, залежить від експозиції взаємодії (год), про що свідчать наведені дані.

Таблиця 3.1 – Залежність електричного струму від експозиції взаємодії,

Напруга, прикладена до рослини, U=60 B
Взаємодія , год	Електричний струм , mkA	Взаємодія , год	Електричний струм , mkA
2	232,8	14	289,8
4	236,1	16	302,3
6	238,4	18	320,4
8	251,3	20	351,6
10	268,4	22	378,8
12	276,5	24	410,3

Визначити апроксимуючу функцію з функцій визначеного типу , , , , , , яка описує залежність електричного струму від експозиції взаємодіїі побудувати її графік.

Розв’язання.

Побудуємо формули нелінійних функціональних залежностей за алгоритмом побудови апроксимуючої функціональної залежності. Знайдемо суми квадратів відхилень вихідних значень і значень апроксимуючих функцій для кожної функціональної залежності, що розглядається.

Гіперболічна функціональна залежність .

Побудуємо лінійну модель , використавши відповідні формули переходу до нових координат (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії , побудуємо таблицю даних , у новій системі координат .

Таблиця 3.2 – Залежність електричного струму від експозиції взаємодії. Гіперболічна функціональна залежність

	0,500	0,250	0,167	0,125	0,100	0,083	0,071	0,063	0,058	0,050	0,045	0,042
	232,8	236,1	238,4	251,3	268,4	276,5	289,8	302,3	320,4	351,6	378,8	410,3

За даними таблиці 3.2 побудуємо розрахункову таблицю.

Таблиця 3.3 – Розрахункова таблиця для гіперболічної залежності

№
1	0,500	232,8	0,250	116,400	232,8	191,10	1738,83
2	0,250	236,1	0,063	59,025	236,1	262,11	676,47
3	0,167	238,4	0,028	39,733	238,4	285,78	2244,72
4	0,125	251,3	0,016	31,413	251,3	297,61	2144,91
5	0,100	268,4	0,010	26,840	268,4	304,71	1318,70
6	0,083	276,5	0,007	23,042	276,5	309,45	1085,56
7	0,071	289,8	0,005	20,700	289,8	312,83	530,34
8	0,063	302,3	0,004	18,894	302,3	315,37	170,70
9	0,056	320,4	0,003	17,800	320,4	317,34	9,38
10	0,050	351,6	0,003	17,580	351,6	318,92	1068,27
11	0,045	378,8	0,002	17,218	378,8	320,21	3433,18
12	0,042	410,3	0,002	17,096	410,3	321,28	7924,11
Сума	1,552	3556,7	0,391	405,740	3556,70	3556,70	22345,16

Знайдемо значення параметрів і лінійної моделі за формулами:

, .

,

.

За формулами переходу знайдемо значення параметрів і гіперболічної функціональної залежності: .

Отже, гіперболічна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд .

Знайдемо значення апроксимуючої функції для вихідних значень змінної і квадрати відхилень вихідних значень і значень апроксимуючої функції . Результати обчислень занесемо в таблицю 3.3.

Сума квадратів відхилень вихідних значень і значень апроксимуючої функції .

Дробово-лінійна функціональна залежність .

Побудуємо лінійну модель , використавши відповідні формули переходу до нових координат (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії , побудуємо нову таблицю , .

Таблиця 3.4 – Залежність електричного струму від експозиції взаємодії. Дробово-лінійна функціональна залежність

	2	4	6	8	10	12	14	16	18	20	22	24
	0,0043	0,0042	0,0042	0,0040	0,0037	0,0036	0,0035	0,0033	0,0031	0,0028	0,0026	0,0024

За даними таблиці 3.4 побудуємо розрахункову таблицю.

Таблиця 3.5 – Розрахункова таблиця для дробово-лінійної залежності

№
1	2	0,0043	4	0,0086	232,8	225,1	59,29
2	4	0,0042	16	0,0169	236,1	234,3	3,24
3	6	0,0042	36	0,0252	238,4	244,4	36
Продовження таблиці
№
4	8	0,0040	64	0,0318	251,3	255,1	14,44
5	10	0,0037	100	0,0373	268,4	267,2	1,44
6	12	0,0036	144	0,0434	276,5	280,3	14,44
7	14	0,0035	196	0,0483	289,8	294,6	23,04
8	16	0,0033	256	0,0529	302,3	310,5	67,24
9	18	0,0031	324	0,0562	320,4	328,4	64
10	20	0,0028	400	0,0569	351,6	348,7	8,41
11	22	0,0026	484	0,0581	378,8	371,3	56,25
12	24	0,0024	576	0,0585	410,3	396,8	182,25
Сума	156	0,0418	2600	0,4941	3556,7	3556,7	530,04

Знайдемо значення параметрів і лінійної моделі за формулами:

,

.

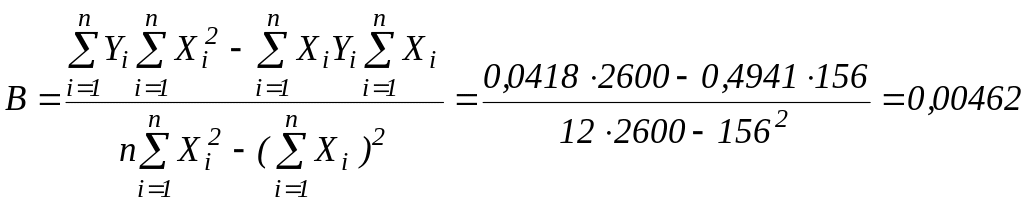За формулами переходу знайдемо значення параметрів і гіперболічної функціональної залежності: .

Дробово-лінійна функціональна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд .

Знайдемо значення апроксимуючої функції для вихідних значень змінної і квадрати відхилень вихідних значень і значень апроксимуючої функції . Результати обчислень занесемо в таблицю 3.5.

Сума квадратів відхилень вихідних значень і значень апроксимуючої функції .

Дробово-раціональна функціональна залежність .

Побудуємо лінійну модель , використавши відповідні формули переходу до нових координат (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії , побудуємо нову таблицю , .

Таблиця 3.6 – Залежність електричного струму від експозиції взаємодії. Дробово-раціональна функціональна залежність

	0,500	0,250	0,167	0,125	0,100	0,083	0,071	0,063	0,058	0,050	0,045	0,042
	0,0043	0,0042	0,0042	0,0040	0,0037	0,0036	0,0035	0,0033	0,0031	0,0028	0,0026	0,0024

За даними таблиці 3.6 побудуємо розрахункову таблицю.

Таблиця 3.7 – Розрахункова таблиця для дробово-раціональної залежності

№
1	0,500	0,0043	0,250	0,0021	232,8	217,44	235,93
2	0,250	0,0042	0,063	0,0011	236,1	263,38	744,20
3	0,167	0,0042	0,028	0,0007	238,4	283,25	2011,52
4	0,125	0,0040	0,016	0,0005	251,3	294,34	1852,44
5	0,100	0,0037	0,010	0,0004	268,4	301,43	1090,98
6	0,083	0,0036	0,007	0,0003	276,5	306,32	889,23
7	0,071	0,0035	0,005	0,0002	289,8	309,86	402,40
8	0,063	0,0033	0,004	0,0002	302,3	312,58	105,68
9	0,056	0,0031	0,003	0,0002	320,4	314,79	31,47
10	0,050	0,0028	0,003	0,0001	351,6	316,58	1226,40
№
11	0,045	0,0026	0,002	0,0001	378,8	317,37	3773,64
12	0,042	0,0024	0,002	0,0001	410,3	319,36	8270,08
Сума	1,552	0,0418	0,391	0,0061	3556,7	3556,7	20633,99

Знайдемо значення параметрів і лінійної моделі за формулами:

,

.

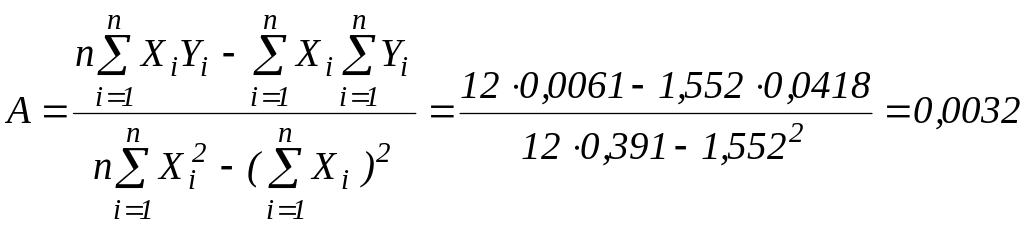За формулами переходу знайдемо значення параметрів і дробово-раціональної функціональної залежності: .

Отже, дробово-раціональна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд .

Знайдемо значення апроксимуючої функції для вихідних значень змінної і квадрати відхилень вихідних значень і значень апроксимуючої функції . Результати обчислень занесемо в таблицю 3.7.

Сума квадратів відхилень вихідних значень і значень апроксимуючої функції .

Ступенева функціональна залежність .

Побудуємо лінійну модель , використавши відповідні формули переходу до нових координат (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії , побудуємо нову таблицю , .

Таблиця 3.8 – Залежність електричного струму від експозиції взаємодії. Ступенева функціональна залежність

	0,693	1,386	1,792	2,079	2,303	2,485	2,639	2,773	2,890	2,996	3,091	3,178
	5,450	5,464	5,476	5,527	5,592	5,622	5,669	5,711	5,770	5,862	5,937	6,017

За даними таблиці 3.8 побудуємо розрахункову таблицю.

Таблиця 3.9 – Розрахункова таблиця для ступеневої залежності

№
1	0,693	5,450	0,480	3,778	232,8	201,95	951,7225
2	1,386	5,464	1,922	7,575	236,1	235,66	0,1936
3	1,792	5,474	3,210	9,808	238,4	258,03	385,3369
4	2,079	5,527	4,324	11,492	251,3	275,11	566,9161
5	2,303	5,592	5,302	12,877	268,4	289,18	431,8084
6	2,485	5,622	6,175	13,971	276,5	301,17	608,6089
7	2,639	5,669	6,965	14,961	289,8	311,44	468,2896
8	2,773	5,711	7,687	15,835	302,3	321,08	352,6884
9	2,890	5,770	8,354	16,676	320,4	329,45	81,9025
10	2,996	5,862	8,974	17,562	351,6	337,46	199,9396
11	3,091	5,937	9,555	18,352	378,8	344,75	1159,403
12	3,178	6,017	10,100	19,122	410,3	351,42	3466,854
Сума	28,305	68,096	73,049	162,010	3556,7	3556,7	8673,663

Знайдемо значення параметрів і лінійної моделі за формулами:

, .

,

.

За формулами переходу параметри і ступеневої функціональної залежності дорівнюють: .

Отже, ступенева залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд .

Знайдемо значення апроксимуючої функції для вихідних значень змінної і квадрати відхилень вихідних значень і значень апроксимуючої функції . Результати обчислень занесемо в таблицю 3.9. Сума квадратів відхилень вихідних значень і значень апроксимуючої функції .

Експоненціальна функціональна залежність .

Побудуємо лінійну модель , використавши відповідні формули переходу до нових координат (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії , побудуємо нову таблицю , .

Таблиця 3.10 – Залежність електричного струму від експозиції взаємодії. Експоненціальна функціональна залежність

	2	4	6	8	10	12	14	16	18	20	22	24
	5,450	5,464	5,476	5,527	5,592	5,622	5,669	5,711	5,770	5,862	5,937	6,017

За даними таблиці 3.10 побудуємо розрахункову таблицю.

Таблиця 3.11 – Розрахункова таблиця для експоненціальної залежності

№
1	2	5,450	4	10,90	232,8	219,13	186,87
2	4	5,464	16	21,86	236,1	230,83	27,77
3	6	5,474	36	32,84	238,4	243,21	23,14
4	8	5,527	64	44,21	251,3	256,12	23,23
5	10	5,592	100	55,92	268,4	269,79	1,93
6	12	5,622	144	67,47	276,5	284,18	58,98
7	14	5,669	196	79,37	289,8	299,34	91,01
8	16	5,711	256	91,38	302,3	315,32	169,52
9	18	5,770	324	103,85	320,4	332,14	137,83
10	20	5,862	400	117,25	351,6	349,89	2,92
11	22	5,937	484	130,61	378,8	368,54	105,27
20	24	6,017	576	144,41	410,3	388,21	487,97
Сума	156	68,096	2600	900,08	3556,7	3556,7	1316,44

Знайдемо значення параметрів і лінійної моделі за формулами:

,

.

За формулами переходу параметри і експоненціальної функціональної залежності дорівнюють: .

Отже, експоненціальна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд .

Знайдемо значення апроксимуючої функції для вихідних значень змінної і квадрати відхилень вихідних значень і значень апроксимуючої функції . Результати обчислень занесемо в таблицю 3.11. Сума квадратів відхилень вихідних значень і значень апроксимуючої функції .

Логарифмічна функціональна залежність .

Побудуємо лінійну модель , використавши відповідні формули переходу до нових координат (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії , побудуємо нову таблицю , .

Таблиця 3.12 – Залежність електричного струму від експозиції взаємодії. Логарифмічна функціональна залежність

	0,69	1,39	1,79	2,08	2,30	2,48	2,64	2,77	2,89	3,00	3,09	3,18
	232,8	236,1	238,4	251,3	268,4	276,5	289,8	302,3	320,4	351,6	378,8	410,3

За даними таблиці 3.12 побудуємо розрахункову таблицю.

Таблиця 3.13 – Розрахункова таблиця для логарифмічної залежності

№
1	0,69	232,8	0,48	161,36	232,8	187,38	2062,86
2	1,39	236,1	1,92	327,30	236,1	232,75	11,25
3	1,79	238,4	3,21	427,16	238,4	259,28	436,11
4	2,08	251,3	4,32	522,56	251,3	278,11	718,86
5	2,30	268,4	5,30	618,01	268,4	292,72	591,26
6	2,48	276,5	6,17	687,08	276,5	304,65	792,34
7	2,64	289,8	6,96	764,80	289,8	314,74	621,87
8	2,77	302,3	7,69	838,15	302,3	323,48	448,45
9	2,89	320,4	8,35	926,08	320,4	331,19	116,32
10	3,00	351,6	8,97	1053,30	351,6	338,08	182,76
11	3,09	378,8	9,55	1170,89	378,8	344,32	1188,95
12	3,18	410,3	10,10	1303,96	410,3	350,01	3634,45
Сума	28,30	3556,7	73,05	8800,65	3556,7	3556,7	10805,48

Знайдемо значення параметрів і лінійної моделі за формулами:

, .

,

.

За формулами переходу параметри і логарифмічної функціональної залежності дорівнюють: , .

Логарифмічна функціональна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд .

Знайдемо значення апроксимуючої функції для вихідних значень змінної і квадрати відхилень вихідних значень і значень апроксимуючої функції . Результати обчислень занесемо в таблицю 3.13.

Сума квадратів відхилень вихідних значень і значень апроксимуючої функції .

Оберемо апроксимуючу функцію за правилом: сума квадратів відхилень вихідних значень і значень апроксимуючої функції мінімальна.

Таблиця 3.14 – Аналітичний критерій обору апроксимуючої функції

Функціональна залежність
Гіперболічна	22345,16
Дробово-лінійна	530,04
Дробово-раціональна	20633,99
Ступенева	8673,663
Експоненціальна	1316,44
Логарифмічна	10805,48

На основі таблиці 3.14 робимо висновок, що для апроксимувати залежність електричного струму від експозиції взаємодії необхідно дробово-раціональною функцією, тому що для неї сума квадратів відхилень вихідних значень і значень апроксимуючої функції мінімальна, .

П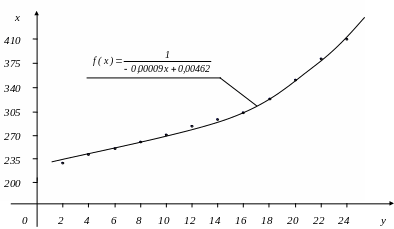 обудуємо графік функціональної залежності електричного струму від експозиції взаємодії.

Р исунок 1 – Графік залежності електричного струму від експозиції

взаємодії і експериментальні дані